SCC(Strongly Connected Component)
2019, Jul 14
- 이번 글에서는 SCC에 대하여 알아보도록 하겠습니다. SCC는 Strongly Connected Componet의 약자입니다.
SCC의 정의 및 용도
- Strongly Connected의 정의 : 모든 정점에서 모든 정점으로 이동할 수 있는 관계
- 무향 그래프에서는 의미가 없고 방향 그래프에서만 의미가 있습니다.
- SCC(Strongly Connected Component) : 그래프를 Stronly Connected 하게 서브 그래프로 나눔
- 각 Component 내부에서는 모든 정점끼리는 서로 이동이 가능하게 됩니다.
- Component 끼리는 Strongly Connected 하지 않습니다.
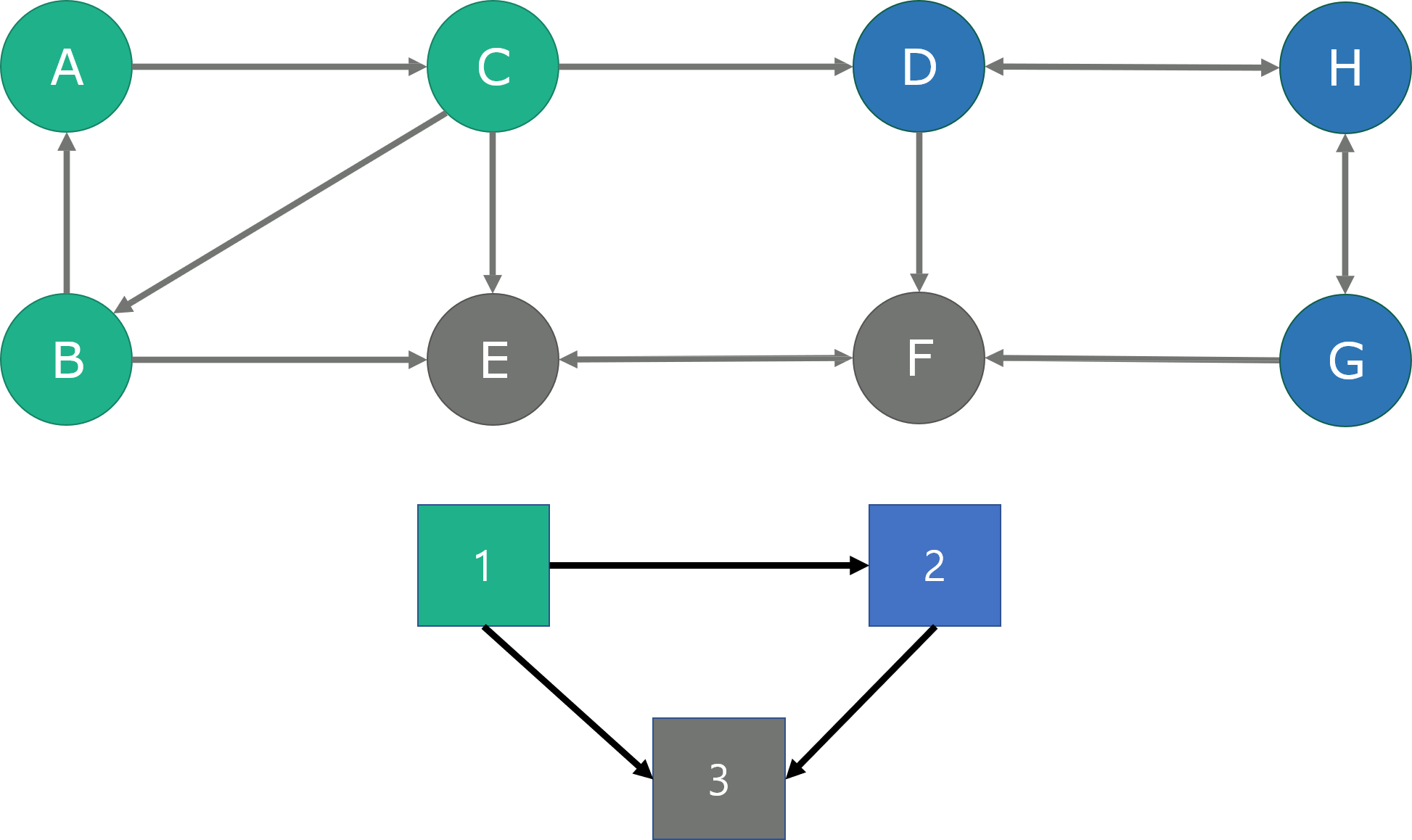
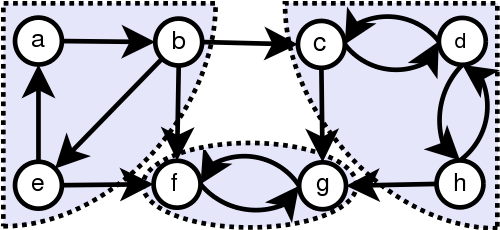
- 위와 같은 방향 그래프에서는 색을 나눈 기준으로 SCC를 만들 수 있습니다.
- 위 그래프에서는 각각 초록색 노드들 끼리, 파란색 노드들 끼리 그리고 회색 노드들 끼리는 모두 연결되어 있어서 이동이 가능합니다. 즉 Strongly Connected 합니다.
- 반면 초록색 Component, 파란색 Component 그리고 회색 Component들 끼리는 Stronly Connected 관계가 아닙니다. 즉, 서로 이동이 가능한 관계는 아닙니다.
- 왜냐하면 만약 SC 관계라면 Component로 분리되지 않기 때문이지요.
- 이 때, 한쪽 Component에서 다른쪽 Component로 이동이 가능한 방향 그래프 관계를 가지게 됩니다. 즉, Component끼리는 DAG(Direct Acyclic Graph) 관계를 가지게 됩니다.
- 위에서 정의한 SCC 내용을 보면 언제 SCC를 사용할 수 있을까요?
- 대표적으로 사용 가능한 케이스는 방향 그래프에서 사이클이 존재하는 경우에 사이클을 제거하고 DAG로 만드는 것입니다.
Kosaraju 알고리즘
- 코사주 알고리즘은 dfs를 이용하여 SCC를 찾는 알고리즘입니다.
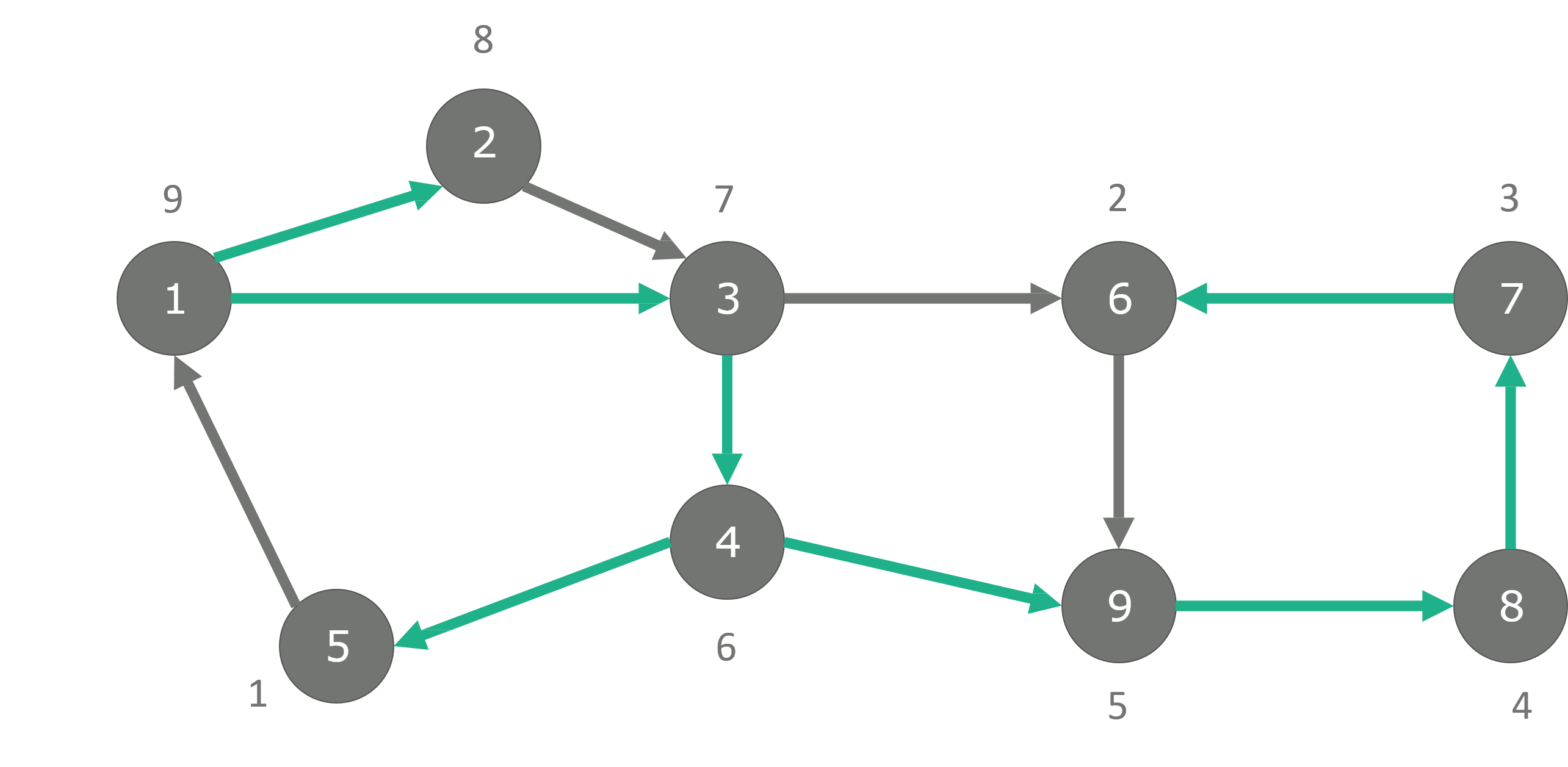
- 위 그림의 노드 안에 적힌 숫자는 노드의 번호이고 노드 위에 적힌 숫자는 dfs 중 스택에서 빠진 순서 입니다.
- 위 그림과 같이 먼저 1번 노드를 먼저 방문하겠습니다.
- 1번 노드를 가장 처음 방문하고 모든 노드를 다 방문하였으므로 1번 노드가 가장 마지막에 스택에 빠지게 되어 9라는 숫자가 노드 위에 적혀져있습니다.
- 1번 노드에서 갈 수 있는 노드 중 3번 노드로 먼저 방문하겠습니다.
- 그다음 4를 방문하겠습니다.
- 그러면 첫번째로 1-3-4-5를 통한 경로는 더 이상 방문 가능한 노드가 없으므로 5번 노드는 스택에서 뻅니다.
- 노드를 스택에서 뺄 때, 스택에서 빠지는 순서를 기록해 둡니다. 즉, 5번 노드는 첫번쨰로 스택에서 빠졌습니다.
- 그 다음으로 계속 탐색을 하면 1-3-4-9-8-7-6 까지 dfs로 탐색할 수 있고 여기서 노드 6은 스택에 빠지게 됩니다. 노드 6은 2번째로 스택에 빠졌습니다.
- 그다음 노드 7은 세번째, 노드 8은 네번째, 노드 9는 다섯 번째, 노드 4는 여섯 번째, 노드 3은 일곱 번째로 빠지게 됩니다.
- 이제 다시 처음 방문한 노드 1로 돌아왔습니다. 이제 1-2 경로를 탐색하고 노드 2를 여덟번째로 스택에서 뺍니다.
- 그리고 마지막으로 노드 1을 아홉 번째로 스택에서 뺌으로 써 탐색을 마칩니다.
- 그 다음으로 방문했던 간선의 방향을 모두 뒤집씁니다.
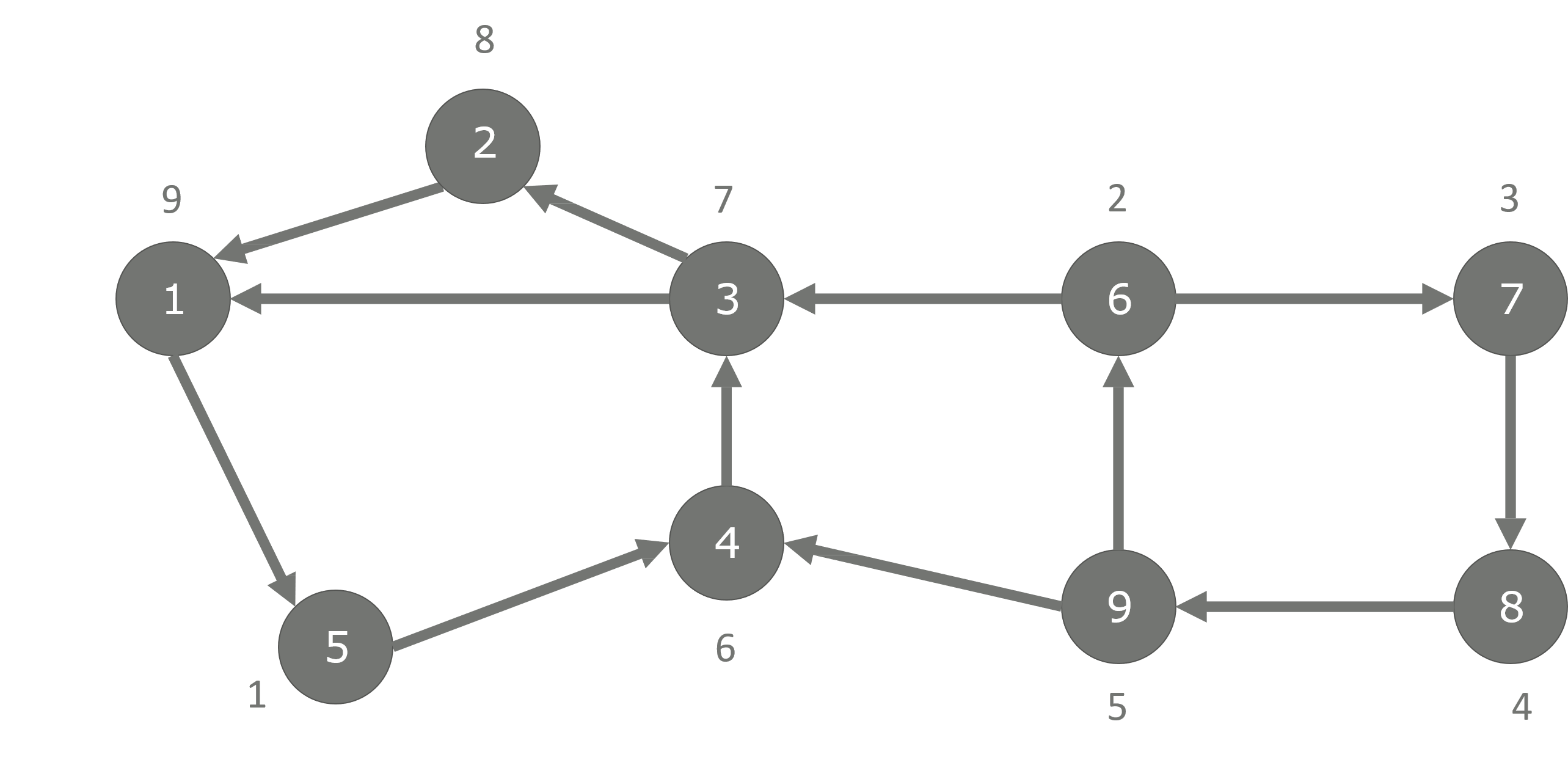
- 위와 같이
간선의 방향을 모두 뒤집은 다음에 가장마지막으로 스택에서 뺀 순서부터 재 dfs탐색을 합니다.- 이번에 dfs를 할 때에는 간선의 방향이 뒤집힌 조건과 탐색 순서가 지정이 되는 조건이 있습니다.
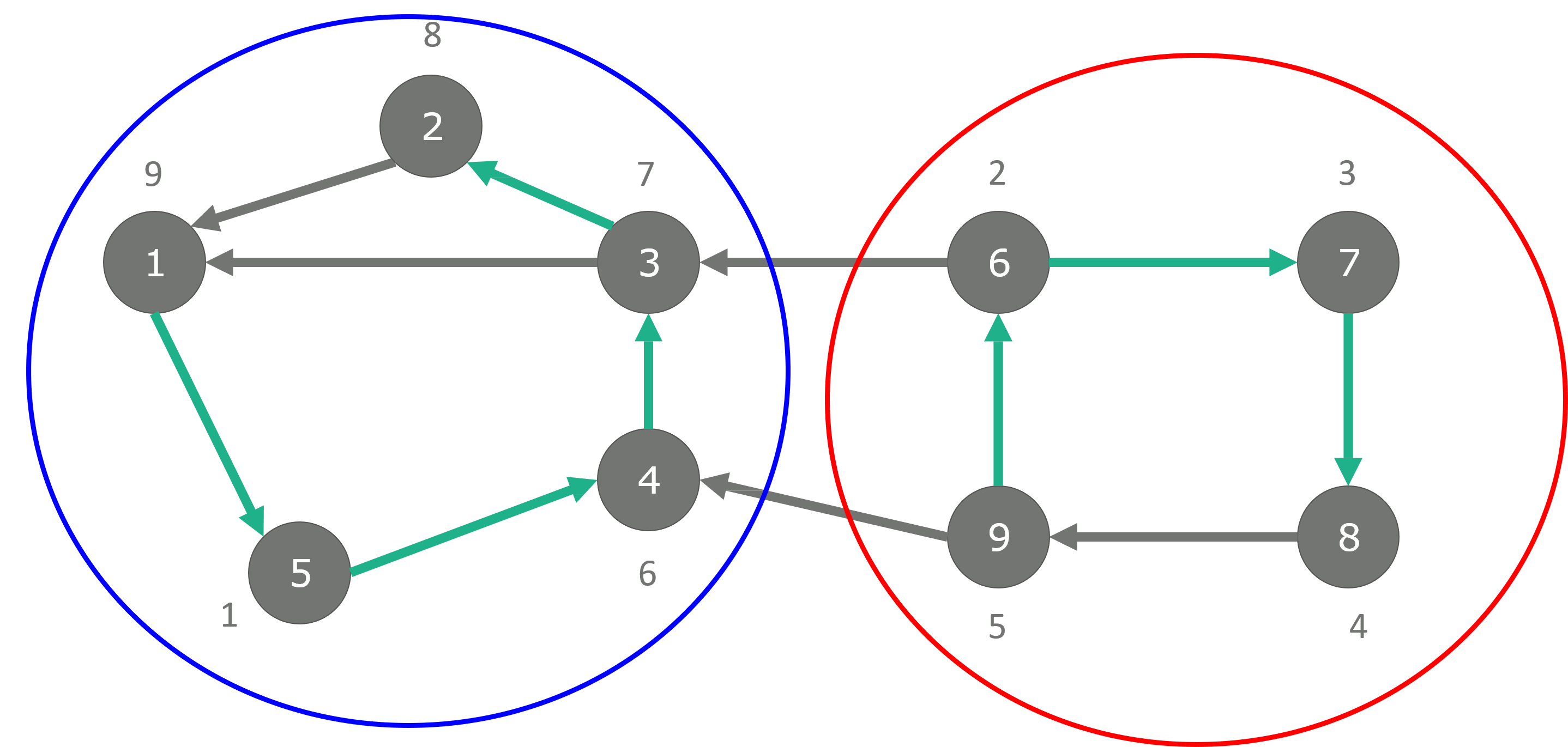
- 먼저 9번째로 스택에서 빠진 노드 1번 부터 탐색을 시작합니다.
- 이 때, 1-5-4-3-2 순서로 방문을 할 수 있고 그 이외의 경로는 없습니다.
- 이 때 만들어진 경로의 노드들이 Strongly Connected 된 Component 중 하나입니다.
- 그 다음으로 탐색할 노드를 살펴보면 8번째, 7번째, 6번째로 스택에서 나온 노드는 이미 방문되었으므로 skip 합니다.
- 5번째로 스택에서 나온 노드를 방문하면 다시 9-6-7-8 경로를 만들 수 있고 이 노드들이 또한 Strongly Connected 된 Component 입니다.
- 따라서 위 그래프에는 2가지의 Strongly Connected한 Component가 있다고 할 수 있습니다.
- SCC 구현 문제
- SCC 구현 코드는 다음과 같습니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> adj_list[10001]; //입력 받은 간선을 저장하는 인접리스트
vector<int> r_adj_list[10001]; //입력 받은 간선을 반대로 저장하는 인접리스트
vector<int> visitied; //노드가 방문되었는지 체크하는 리스트
vector<int> component; //노드의 component 번호를 저장하는 리스트
vector<int> order; // 스택에 빠진 순서대로 저장하는 리스트
// dfs를 하면서 스택에서 사라질 때, order에 추가합니다.
void dfs(int x) {
visitied[x] = true;
for (int y : adj_list[x]) {
if (!visitied[y]) {
dfs(y);
}
}
order.push_back(x);
}
// 방향을 거꾸로 저장한 리스트를 dfs하면서 component를 그룹화 합니다.
void dfs_rev(int x, int cnt) {
visitied[x] = true;
// x노드를 cnt 그룹으로 만들어 줍니다.
component[x] = cnt;
for (int y : r_adj_list[x]) {
if (!visitied[y]) {
dfs_rev(y, cnt);
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, M;
cin >> N >> M;
while (M--) {
int u, v;
cin >> u >> v;
adj_list[u].push_back(v);
// 방향을 반대로 구성한 간선을 저장합니다.
r_adj_list[v].push_back(u);
}
// 인접리스트를 dfs 수행
visitied = vector<int>(N + 1);
for (int i = 1; i <= N; ++i) {
if (!visitied[i]) {
dfs(i);
}
}
// 가장 마지막에 스택에 빠진 리스트를 가장 앞으로 오도록 reverse
reverse(order.begin(), order.end());
// 방향을 거꾸로 저장한 인접리스트를 dfs 수행
visitied = vector<int>(N + 1);
component = vector<int>(N + 1);
int cnt = 0;
for (int x : order) {
if (component[x] == 0) {
cnt += 1;
dfs_rev(x, cnt);
}
}
// 아래는 문제 솔루션 포맷에 맞게 출력하기 위한 코드
cout << cnt << '\n';
vector<vector<int>> ans(cnt);
for (int i = 1; i <= N; i++) {
ans[component[i] - 1].push_back(i);
}
for (int i = 0; i < cnt; i++) {
sort(ans[i].begin(), ans[i].end());
}
sort(ans.begin(), ans.end());
for (int i = 0; i < cnt; i++) {
for (int x : ans[i]) {
cout << x << " ";
}
cout << "-1\n";
}
}