트리 순회 (전위 순회, 중위 순회, 후위 순회)

알고리즘 관련 글 목차

• 참조 : https://m.blog.naver.com/rlakk11/60159303809

• 트리 관련 대표적인 문제로 트리 순회가 있습니다. 이번 글에서는 전위 순회, 중위 순회, 후위 순회에 대하여 간단하게 알아보도록 하겠습니다.
• 전/중/후위에 해당하는 순서는 각각 노드를 기준으로 나뉘게 됩니다. 먼저 간단하게 정의를 살펴보겠습니다.
  • 전위 순회 : 매번 노드 부터 먼저 방문한 뒤, left 엣지, right 엣지 순서로 선택됩니다.
  • 중위 순회 : 매번 left 엣지 부터 먼저 선택된 다음, left 엣지를 선택할 수 없으면 노드를 방문하고 그 다음 right 엣지를 선택합니다.
  • 후위 순회 : 매번 left 엣지 부터 먼저 선택하고 그 다음 right 엣지를 선택합니다. 선택할 수 있는 엣지가 없으면 노드를 방문합니다.

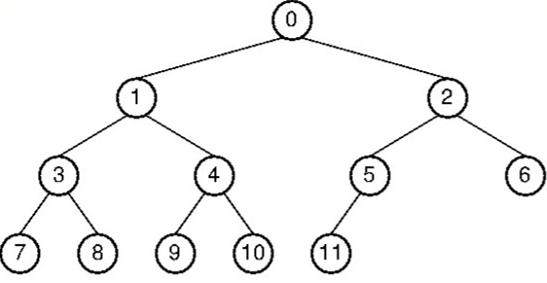
• 위 트리 그래프를 전위, 중위, 후위 순서로 탐색해 보겠습니다. 출발은 루트인 0에서 시작하겠습니다.
• 탐색을 할 때에는 항상 머릿속에 노드, left 엣지, right 엣지의 방문 순서를 생각하면 되겠습니다.

• 전위 순회 : 노드 → left 엣지 → right 엣지 순서로 방문합니다.
• 위 예제 탐색 순서 : 0 → 1 → 3 → 7 → 8 → 4 → 9 → 10 → 2 → 5 → 11 → 6

void preorder_traverse(node *t){
	visit(t);
	preorder_traverse(t->left);
	preorder_traverse(t->right);
}

• 앞에서 설명하였듯이 노드 → left 엣지 → right 엣지의 방문 순서를 생각하면서 순회를 하면 아래와 같습니다.
• 먼저 전위 순회는 노드 부터 방문하기 때문에 root 노드를 방문하고 left 엣지로 갑니다. 그 다음 부터 다시 노드부터 방문하고 최종적으로 leaf 까지 방문합니다/ 마지막 left 엣지를 방문한 이후 부터는 right 엣지를 방문하면서 순회합니다.
• 이 순서는 위의 코드를 통해서 그 방문 순서를 알 수 있습니다.

• 중위 순회 : left → 노드 → right 순서로 방문합니다.
• 위 예제 탐색 순서 : 7 → 3 → 8 → 1 → 9 → 4 → 10 → 0 → 11 → 5 → 2 → 6

void inorder_traverse(node *t){
	inorder_traverse(t->left);
	visit(t);
	inorder_traverse(t->right);
}

• 전위 순회와는 다르게 left 엣지 부터 먼저 선택하며 leaf 까지 계속 left 엣지부터 먼저 선택합니다. 더 이상 선택할 수 없으면 그 때, 노드를 방문하게 됩니다.
• 위 예제에서 leaf 노드인 7 까지 순회하였을 때, 더 선택할 수 있는 left 엣지가 없으므로 노드인 7이 방문되고 그 다음 right 엣지를 선택해야 합니다. 이 때에도 right 엣지는 없으므로 그 상위 노드로 리턴 됩니다.
• 상위 노드인 3을 그 다음 방문하고 이제 right 엣지를 선택하게 됩니다.
• 이와 같은 방법으로 중위 순회를 진행합니다.

• 후위 순회 : left → right → 노드 순서로 방문합니다.
• 위 예제 탐색 순서 : 7 → 8 → 3 → 9 → 10 → 4 → 1 → 11 → 5 → 6 → 2 → 0

void postorder_traverse(node *t){
	postorder_traverse(t->left);
	postorder_traverse(t->right);
	visit(t);
}

• 후위 순회는 left 엣지와 right 엣지를 모두 선택한 다음에 마지막으로 노드를 방문을 하게 됩니다. 따라서 가장 왼쪽 leaf 케이스를 보면 7번 노드와 8번 노드가 먼저 방문된 다음에 3번 노드가 방문되는 것을 확인할 수 있습니다.

알고리즘 관련 글 목차