Trie
2019, Oct 11
- 이번 글에서는 문자열 알고리즘의 하나인
trie에 대하여 알아보도록 하겠습니다. trie관련 알고리즘을 익혔으면 링크에서trie관련 문제를 찾아 한번 풀어보시길 바랍니다.
목차
-
Trie 알고리즘의 필요성
-
Trie 알고리즘
-
C++을 이용한 Trie 알고리즘 구현
Trie 알고리즘의 필요성
Trie알고리즘은 문자열 비교를 할 때 효율적으로 사용할 수 있습니다.- 숫자를 비교할 때에는
O(1)의 상수시간 만에 비교할 수 있습니다. 반면 문자열을 비교할 때에는O(길이)의 시간이 걸립니다. - 그러면 N개의 숫자를 담고 있는 BST(Binary Search Tree)에서는 특정 숫자를 찾는 데
O(logN)의 복잡도를 가지지만 문자열 N개를 담고 있는 BST에서는 특정 문자열을 검색하는 데 걸리는 시간은O(길이 * logN)입니다. - BST를 만드는 시간 복잡도를 살펴보면 숫자의 경우에는
O(NlogN)인 반면에 문자열의 경우O(길이*NlogN)이 됩니다. 생각보다 비효율적이게 됩니다. - 비교를 할 때에는 트리 구조를 만드는 것이 효율적이지만 단순한 트리 구조를 이용하여 문자열을 비교하면 꽤나 비효율적이 됩니다.
- 이런 문제를 개선하기 위하여 등장한 것이
Trie알고리즘입니다.
Trie 알고리즘
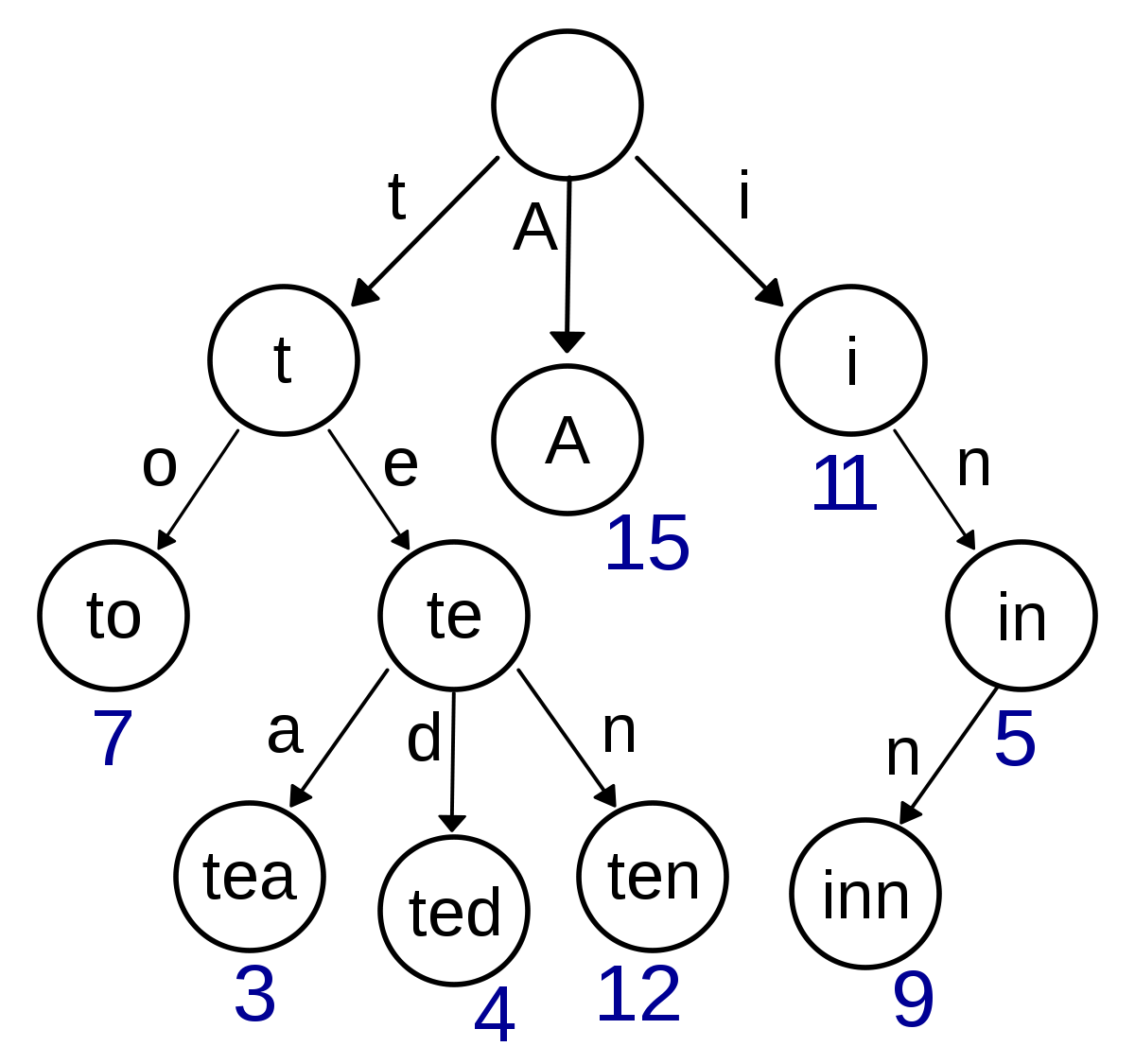
- 단어 셋이 {A, to, tea, ted, ten, i, in, inn} 이 있다고 가정하고 Trie 구조의 트리를 만들어 보면 위와 같습니다.
- 이 트리에서 depth는 문자열의 길이를 뜻하게 됩니다.
trie의 이런 구조로 인하여 또 다른 이름으로prefix tree라고도 하는데 그 이유는 부모 노드가 자식 노드의 prefix가 되기 때문입니다.- 여기서 발생하는 문제점 한가지는 위 그림의 노드 중에 te라는 노드는 실제 단어셋에 존재하지는 않지만 노드로 구성되었습니다.
- 따라서 이 문제를 해결하기 위하여 각 노드에 이 노드가 실제 단어 셋에 있는 단어인지 아닌지를 표시해주는
flag가 필요합니다. 이것을valid라고 하고valid = true이면 실제 단어셋에 존재하는 문자열이라고 표현해줍니다.
C++을 이용한 Trie 알고리즘 구현
-
vector를 이용하여 구현하는 방법
#include <iostream>
#include <string>
#include <vector>
using namespace std;
// 자식 노드의 갯수로 총 단어의 갯수에 해당합니다.
// 만약 숫자만 있으면 (0 ~9) 사이즈는 10, 알파벳 소문자만 있으면 26으로 정하면 됩니다.
const int char_size = 26;
// Trie vector의 element
struct Node {
// 실제 단어에 해당하는 노드인지 유무
bool valid;
// char_size 만큼의 크기를 가지는 자식 노드
vector<int> children;
Node() {
valid = false;
children.assign(char_size, -1);
}
};
// trie vector를 초기화 합니다.
// root를 생성하고 root의 node 번호는 0이 됩니다.
int Init(vector<Node>& trie) {
Node x;
trie.push_back(x);
return (int)trie.size() - 1;
}
// 문자열s가 입력되면 trie에 구성합니다.
void Add(vector<Node>& trie, int node, string& s, int index) {
// index는 trie에서의 depth에 해당합니다.
// index(depth)가 문자열의 길이와 같아지면 이 노드에 입력된 문자열을 할당합니다.
if (index == s.size()) {
trie[node].valid = true;
return;
}
// 현재 인덱스에 해당하는 문자를 숫자로 매칭시킵니다.
int c = s[index] - 'a';
// 현재 노드의 자식 노드 중 c에 해당하는 노드가 생성되지 않았다면 생성합니다.
if (trie[node].children[c] == -1) {
// trie에 새로운 노드를 생성해 주고 그 노드의 번호를 리턴 받습니다.
int next = Init(trie);
// 리턴 받은 노드 번호를 c번 자식 노드에 할당해 줍니다.
trie[node].children[c] = next;
}
// 아직 index가 문자열 전체 길이만큼 탐색하지 않았으므로 문자열의 다음 인덱스를 탐색합니다.
// 즉, trie에서 더 깊은 depth 까지 문자열을 구성하는 작업을 재귀를 통하여 반복합니다.
Add(trie, trie[node].children[c], s, index + 1);
}
// trie에서 특정 문자열 s를 찾는 작업을 합니다.
// trie를 사전에 구성하였기 때문에 O(문자열 s의 길이)만에 찾을 수 있습니다.
bool TrieSearch(vector<Node>& trie, int node, string& s, int index) {
//문자열 인덱스의 길이 만큼 trie를 탐색한 경우,
if (index == s.size()) {
// 현재 노드의 valid가 유효하다면 단어가 존재합니다.
if (trie[node].valid) {
return true;
}
else {
return false;
}
}
bool ret = false;
int c = s[index] - 'a';
// c번 자식 노드가 구성되어 있다면 계속 트리를 탐색합니다.
// 만약 구성되지 않았다면 trie에 찾는 문자열은 없습니다.
if (trie[node].children[c] != -1) {
ret = TrieSearch(trie, trie[node].children[c], s, index + 1);
}
return ret;
}
int main() {
// Trie를 만들 전체 단어 셋
vector<string> dic = { "a", "to", "tea", "ted", "i", "in", "inn" };
// 테스트 해 볼 단어 셋
vector<string> test = { "a", "to", "inn", "tee", "aee", "vae"};
// Trie를 저장할 vector
vector<Node> trie;
// Trie 초기화를 위한 root 삽입
int root = Init(trie);
// 단어셋을 Trie에 삽입
for(auto word : dic){
Add(trie, root, word, 0);
}
// 테스트 단어 셋을
for (auto word : test) {
cout << word << ": ";
if (TrieSearch(trie, root, word, 0)) {
cout<<"Exist"<< endl;
}
else {
cout<<"Not exist"<<endl;
}
}
}
-
트리 구조 (링크드 리스트)를 이용하여 구현하는 방법