전통적 경제학 vs 게임 이론

출처 : 유니와이즈 게임이론

이번 글에서는 전통적 경제학과 게임이론이 어떻게 다른지 비교해 보도록 하겠습니다.

• 전통적 경제학 : 개인의 최적 의사결정의 합은 사회 전체의 최적을 만듭니다.
• 전통적 경제학에서의 경제 주체에 대한 가정
  • 경제 주체 = 경기자
  • 효용 함수 = 자신의 소비수준에 의한 결정
  • 경기자는 생산자 또는 소비자가 됩니다. : 이 때 전략은 생산량 또는 소비량이 됩니다.
    • 효용 함수에서 $x_{i}^{j}$ 는 i번째 소비자가 j를 소비한다는 것을 뜻합니다.
    • ·$max_{x_{1}^{1}, x_{1}^{2}}u(x_{1}^{1}, x_{1}^{2}), s.t. p_{1}x_{1}^{1} + p_{2}x_{1}^{2} = m_{1}$
      • 이 때, $p_{i}$는 i번째 재화의 가격, $m_{i}$는 i번째 경기자의 소득입니다.
      • 1번 소비자가 1번 물건과 2번 물건을 소비할 때의 효용함수.
    • ·$max_{x_{2}^{1}, x_{2}^{2}}u(x_{2}^{1}, x_{2}^{2}), s.t. p_{1}x_{2}^{1} + p_{2}x_{2}^{2} = m_{2}$
      • 2번 소비자가 1번 물건과 2번 물건을 소비할 때의 효용함수.
  • 이윤 함수 = 자신의 생산량에 의한 결정
    • ·$max_{x_{1}^{1}, x_{1}^{2}} \pi(x_{1}^{1}, x_{1}^{2}), s.t. p_{1}x_{1}^{1} + p_{2}x_{1}^{2} - C_{1}(x_{1}^{1} + x_{1}^{2}) = \pi_{1}$
      • 이 떄, $p_{i}$는 i번째 재화의 가격, $C_{i}$는 비용 함수라고 가정합니다.
    • ·$max_{x_{2}^{1}, x_{2}^{2}} \pi(x_{2}^{1}, x_{2}^{2}), s.t. p_{1}x_{2}^{1} + p_{2}x_{2}^{2} - C_{2}(x_{2}^{1} + x_{2}^{2}) = \pi_{2}$
  • 효용 함수와 이윤함수 모둗 각 경기자의 선택만 고려하므로 전략적 상황에 대한 고려가 불가능합니다.

• 전략적 상황을 고려할 때
  • 효용 극대화
    • ·$max_{x_{1}^{1}, x_{1}^{2}} u(x_{1}^{1}, x_{1}^{2}, x_{2}^{1}, x_{2}^{2}) s.t. p_{1}x_{1}^{1} + p_{2}x_{1}^{2} = m_{1}$
    • ·$max_{x_{2}^{1}, x_{2}^{2}} u(x_{2}^{1}, x_{2}^{2}, x_{1}^{1}, x_{1}^{2}) s.t. p_{1}x_{2}^{1} + p_{2}x_{2}^{2} = m_{2}$
  • 이윤 극대화
    • ·$max_{x_{1}^{1}, x_{1}^{2}} \pi(x_{1}^{1}, x_{1}^{2}, x_{2}^{1}, x_{2}^{2}) s.t. p_{1}x_{1}^{1} + p_{2}x_{1}^{2} - C_{1}(x_{1}^{1} + x_{1}^{2}) = \pi_{1}$
    • ·$max_{x_{2}^{1}, x_{2}^{2}} \pi(x_{2}^{1}, x_{2}^{2}, x_{1}^{1}, x_{1}^{2}) s.t. p_{1}x_{2}^{1} + p_{2}x_{2}^{2} - C_{2}(x_{2}^{1} + x_{2}^{2}) = \pi_{2}$
  • 전략적 상황을 고려할 때, 수요, 공급함수는 상대방 전략을 고려합니다.

• 다변수 함수의 극대값과 극소값에 대하여 구해보겠습니다.
• 다변수 함수의 극대값과 극소값은 각 변수에 대하여 편미분한 결과들을 연립방정식 놓습니다.
• 연립방정식을 풀어서 동시에 만족하는 해를 구하면 됩니다.
  • 예를 들어, $x_{1}, x_{2}$의 변수를 가지고 목적함수가 $Y$ 일 때,
  • 연립방정식으로 $\frac{Y}{\partial x_{1}} = 0, \frac{Y}{\partial x_{2}} = 0$을 풀어서 나온 해가 다변수 함수의 극대/극소 값입니다.

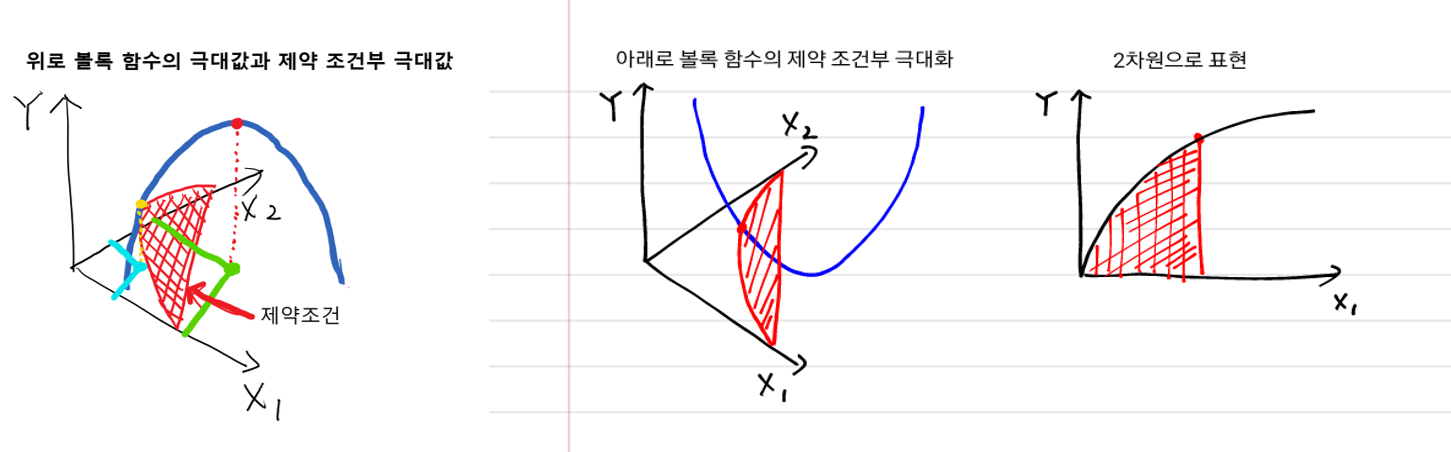
• 위로 볼록한 함수를 보면 전체 영역의 극대값을 구할 수 있지만, 제약 조건이 걸린 경우 그 조건 하의 극대값을 구할 수 있습니다.
• 아래로 볼록한 함수의 경우 전체 영역의 극대값을 구할 수는 없지만, 제약 조건 하의 조건부 극대화는 구할 수 있습니다.
  • 2차원 그래프로 나타내면 좀 더 명확하게 이해가 됩니다.
• 3차원 영역에서는 제약 조건부 극대화 값을 어떻게 찾을까요?
  • 라그랑주 승수법을 이용하여 찾을 수 있습니다.
• 라그랑주 승수법이란?
  • 위의 그래프의 위로 볼록 함수에서 제약 조건 극대화를 구한다고 가정해 봅시다.
  • 최적화 목적은 $max \ y = u(x_{1}, x_{2}), s.t. p_{x_{1}}x_{1} + p_{x_{2}}x_{2} = m$ 입니다.
  • 라그랑주 승수법은 $\mathcal L$ = object function + $\lambda \cdot$ (제약 조건) 으로 정의합니다.
  • object function 뒤의 term은 상수 $\lambda$ 에 제약 조건을 항상 만족하되는 상태를 곱한것 입니다.
    • 소비자 이론에서는 지출과 소득의 합은 같다로 보면 즉, $p_{x_{1}}x_{1} + p_{x_{2}}x_{2} = m$ 이고 (m=소득, p=가격, x=소비량)
    • 정리하면 $\lambda(m - p_{x_{1}}x_{1} - p_{x_{2}}x_{2})$ 를 object function에 더하여 제약 조건을 추가합니다.
  • 라그랑주 승수법으로 정의한 식을 각 변수와 람다에 대하여 편미분을 하고 그 결과 = 0으로 하여 연립 방정식을 풀이합니다.
    • 즉, $\frac{\partial \mathcal L}{\partial x_{1}} = 0, \frac{\partial \mathcal L}{\partial x_{2}} = 0, \frac{\partial \mathcal L}{\partial \lambda} = 0$ 이 됩니다.
    • 이 때 $\frac{\partial \mathcal L}{\partial \lambda} = 0$는 제약조건 = 0이 나오게 됩니다.
      • 제약 조건이 항상 만족하도록 하기 위해서 마지막 term을 붙여 준 것입니다.
  • 라그랑주 승수법을 편미분 한것과 목적 함수를 편미분하는 것의 차이는 무엇일까요?
    • 목적 함수를 편미분 하는것
      • ·$\frac{\partial u}{\partial x_{1}} = 0, \frac{\partial u}{\partial x_{2}} = 0$ 입니다.
      • 이 때, 순간 기울기는 $x_{1}$ 방향에서도 0, $x_{2}$ 방향에서도 동시에 0을 만족하며 이 때가 극대/극소점이 됩니다.
    • 라그랑주 승수법을 편미분 하는것
      • ·$\mathcal L = u(x_{1}, x_{2}) + \lambda(m-p_{x_{1}}x_{1}-p_{x_{2}}x_{2})$ 일 때,
      • 제약 조건을 일반식으로 $g^{0} - g(x_{1}, x_{2}) = 0$으로 표현한 후, 각 변수에 대하여 편미분을 해보겠습니다.
      • ·$\frac{\partial \mathcal L}{\partial x_{1}} = \frac{\partial u}{\partial x_{1}} - \lambda \frac{\partial g}{\partial x_{1}} = 0$ 으로 편미분 하고
        • 우변을 정리하면 $\frac{\partial u}{\partial x_{1}} = \lambda \frac{\partial g}{\partial x_{1}}$ 입니다.
      • ·$\frac{\partial \mathcal L}{\partial x_{2}} = \frac{\partial u}{\partial x_{2}} - \lambda \frac{\partial g}{\partial x_{2}} = 0$ 으로 편미분 합니다.
        • 우변을 정리하면 $\frac{\partial u}{\partial x_{2}} = \lambda \frac{\partial g}{\partial x_{2}}$ 입니다.
      • 이 때, 목적함수를 편미분 한것의 비율과 제약 조건을 편미분 한것의 비율이 일치하는 지점이 제약 조건하의 극대/극소점이 됩니다.
        • 즉, $\frac{\partial u / \partial x_{1}}{\partial u / \partial x_{2}} = \frac{\partial g / \partial x_{1}}{\partial g / \partial x_{2}}$ 으로
        • 좌변(목적함수를 편미분 한것들의 비율) = 우변(제약 조건을 편미분 한것의 비율)
      • 그리고 제약 조건에 관하여 $\frac{\partial \mathcal L}{\partial \lambda} = p_{x_{1}}x_{1} + p_{x_{2}}x_{2} - m = 0$ 으로 앞에서 설명하였듯이 제약조건을 항상 만족할 수 있도록 합니다.
      • 최종적으로 위 편미분 결과들의 연립방정식을 풀면 해를 구할 수 있습니다.
        
        

전통적 경제학과 게임 이론에서의 효용 극대화 문제 비교

1) 전통적 경제학에서의 효용극대화 문제

• 문제 : $u_{1} = x_{1}^{0.5}y_{1}^{0.5}, u_{2} = x_{2}^{0.5}y_{2}^{0.5}$
  • 두 식 모두 각자의 효용함수는 상대방의 전략과 무관합니다.
  • 두 식이 같은 형태이므로 $u_{1}$에 대하여만 풀어보겠습니다.
  • ·$\mathcal L = x_{1}^{0.5}y_{1}^{0.5} + \lambda(m -p_{x_{1}}x_{1} -p_{y_{1}}y_{1})$
  • ·$\frac{\partial \mathcal L}{\partial x_{1}} = \frac{1}{2} x_{1}^{-0.5}y_{1}^{0.5} - \lambda p_{x_{1}}$
    • 우변을 정리하면, $\frac{1}{2} x^{-0.5}y^{0.5} = \lambda p_{x_{1}}$
  • ·$\frac{\partial \mathcal L}{\partial y_{1}} = \frac{1}{2} x_{1}^{0.5}y_{1}^{-0.5} - \lambda p_{y_{1}}$
    • 우변을 정리하면, $\frac{1}{2} x_{1}^{0.5}y_{1}^{-0.5} = \lambda p_{y_{1}}$
  • 목적함수와 제약조건의 편미분 결과의 비율이 같아야 하므로 두 식의 비율을 살펴보면
    • ·$\frac{ \frac{1}{2} x^{-0.5}y^{0.5} }{ \frac{1}{2} x_{1}^{0.5}y_{1}^{-0.5} } = \frac{ \lambda p_{x_{1}} }{ \lambda p_{y_{1}} }$
      • 정리하면 $y_{1} = \frac{ p_{x_{1}} }{ p_{y_{1}} }x_{1}$ 입니다.
      • 이 식을 1번식이라고 하겠습니다.
  • ·$\frac{\partial \mathcal L}{\partial \lambda} = m -p_{x_{1}}x_{1} -p_{y_{1}}y_{1} = 0$
    • 이 식을 2번식이라고 하겠습니다.
  • 1번식과 2번식을 연립방정식으로 풀어보면 $x = \frac{m}{ 2p_{x_{1}} }, y = \frac{m}{ 2p_{y_{1}} }$이 됩니다.

2) 게임 이론에서의 효용극대화 문제

• 문제 : $u_{1} = x_{1}^{0.5}y_{1}^{0.5} - x_{1}x_{2}, u_{2} = x_{2}^{0.5}y_{2}^{0.5} - x_{1}x_{2}$
  • 두 식 $u_{1}, u_{2}$ 모두 자신의 소비가 많을 수록 효용이 높아지지만($x_{i}^{0.5}y_{i}^{0.5}$) 그에 비례하게 상대방의 효용이 커질수록 나의 효용은 떨어집니다.($-x_{1}x_{2}$)
  • 두 식이 같은 형태이므로 $u_{1}$에 대하여만 풀어보겠습니다.
  • ·$max \ \mathcal L = x_{1}^{0.5}y_{1}^{0.5} - x_{1}x_{2} + \lambda(m - p_{x_{1}}x_{1} - p_{y_{1}}y_{1})$
  • ·$\frac{\partial \mathcal L}{\partial x_{1}} = \frac{1}{2} x_{1}^{-0.5}y_{1}^{0.5} - x_{2} - \lambda p_{x_{1}} = 0$
    • 우변을 정리하면, $\frac{1}{2} x_{1}^{-0.5}y_{1}^{0.5} - x_{2} = \lambda p_{x_{1}}$
  • ·$\frac{\partial \mathcal L}{\partial y_{1}} = \frac{1}{2} x_{1}^{0.5}y_{1}^{-0.5} - \lambda p_{y_{1}} = 0$
    • 우변을 정리하면, $\frac{1}{2} x_{1}^{0.5}y_{1}^{-0.5} = \lambda p_{y_{1}}$
  • 목적함수와 제약조건의 편미분 결과의 비율이 같아야 하므로
    • ·$\frac{\frac{1}{2} x_{1}^{-0.5}y_{1}^{0.5} - x_{2}}{\frac{1}{2} x_{1}^{0.5}y_{1}^{-0.5}} = \frac{\lambda p_{x_{1}}}{\lambda p_{y_{1}}}$
    • ·$\frac{y_{1}}{x_{1}} - \frac{x_{2}}{\frac{1}{2} x_{1}^{0.5}y_{1}^{-0.5}} = \frac{p_{x_{1}}}{p_{y_{1}}}$
      • 식을 정리하면, $\frac{y_{1}}{x_{1}} - 2\sqrt{frac{y_{1}}{x_{1}}}x_{2} = \frac{p_{x_{1}}}{p_{y_{1}}}$ 입니다.
      • 위 정리한 식을 1번식이라고 하겠습니다.
  • 제약조건 식을 도출하기 위해 $\lambda$에 대하여 편미분한 결과를 정리하면
    • ·$p_{x_{1}}x_{1} - p_{y_{1}}y_{1} = m$ 입니다.
    • 위 정리한 식을 2번식이라고 하겠습니다.
  • 1번식과 2번식을 연립방정식을 풀면 전략적 상황의 제약 조건 극대화 솔루션이 됩니다.
  • 식이 굉장히 더러워서… 풀이는 생략하겠습니다.
  • 여기서 중요한 것은 비전략적 상황에 비하여 전략적 상황의 식에 $- 2\sqrt{ \frac{ y_{1} }{ x_{1} } } x_{2}$ 이 추가된 것이 중요합니다.
    • 이 term이 전략적 상황을 고려했을 때의 차이이고 곱해지는 $x_{2}$ 로 인하여 상대방의 전략 또한 고려되어 지게 됩니다.