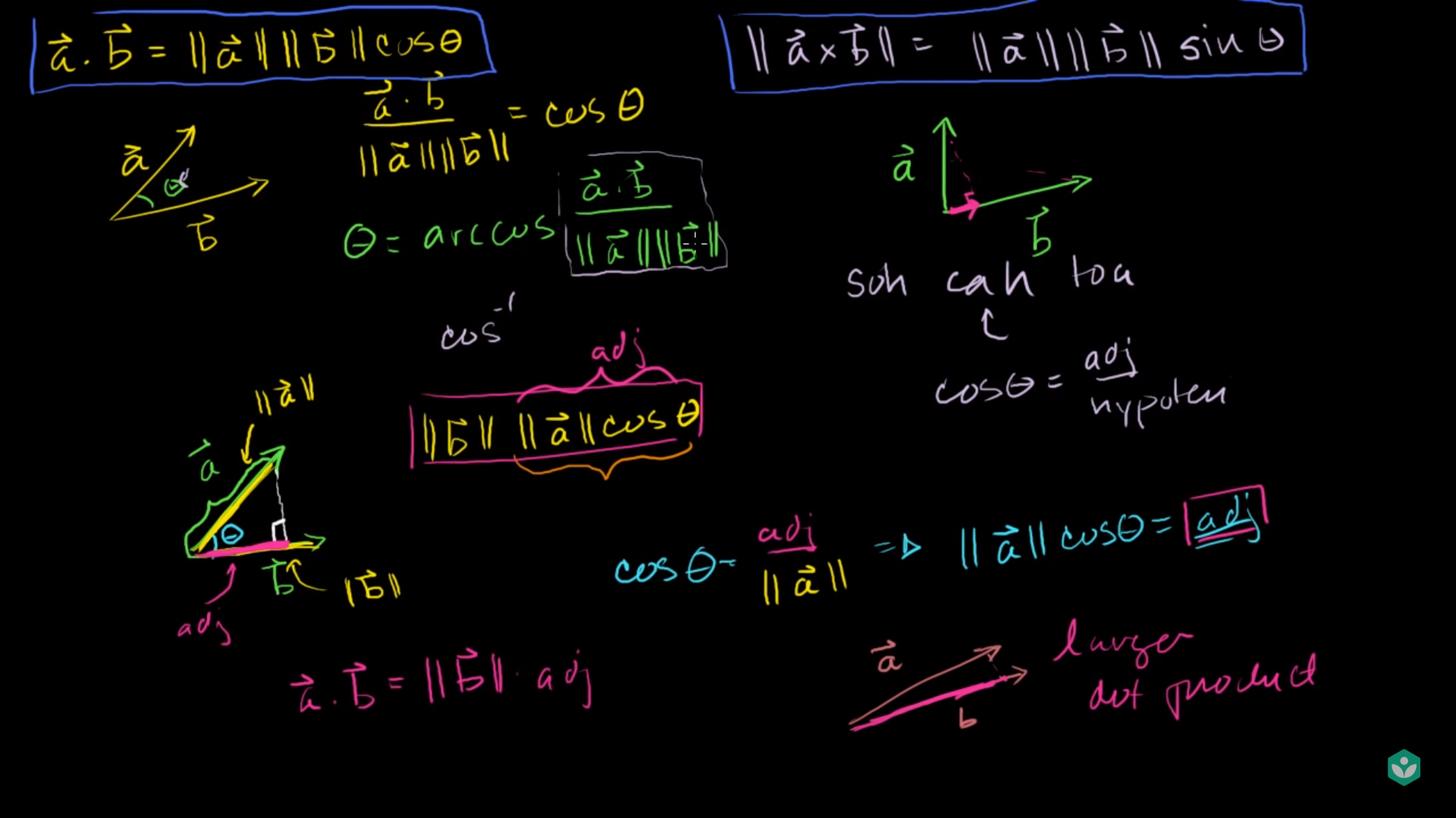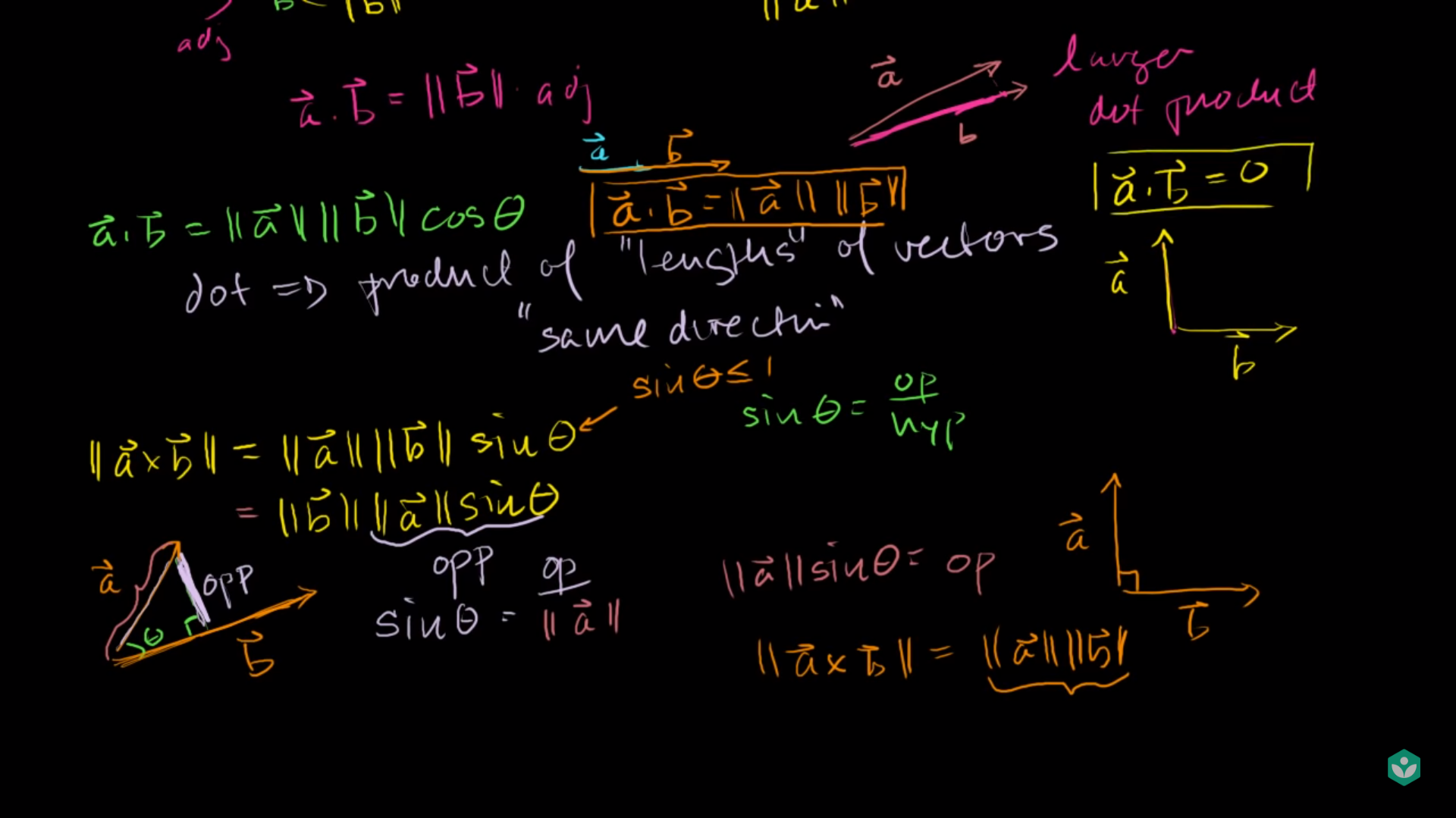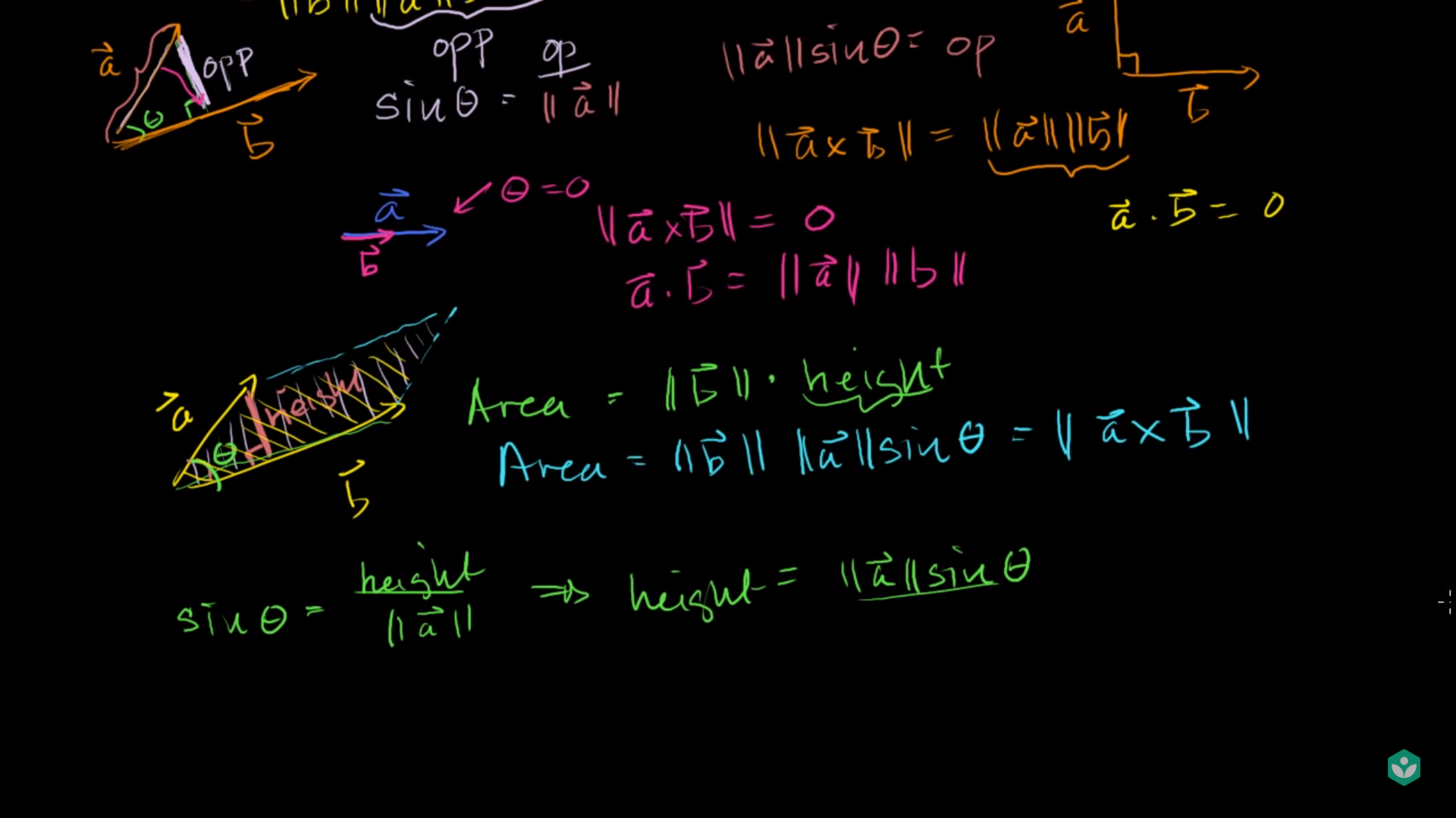외적과 값의 사인값 사이의 관계

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

• 선형대수학 전체 글 목록

• 이번 글에서는 내적(dot product)와 외적(cross product)가 가지는 의미에 대하여 알아보도록 하겠습니다.
• 앞에서 살펴본 바와 같이 내적과 외적은 다음 성질을 가집니다.
  • 내적 : \(\vec{a} \cdot \vec{b} = \Vert \vec{a} \Vert \ \Vert \vec{b} \Vert cos\theta\)
  • 외적 : \(\Vert \vec{a} \times \vec{b} \Vert = \Vert \vec{a} \Vert \ \Vert \vec{b} \Vert sin\theta\)
• 내적과 외적의 성질이 무슨 의미를 가지는 지 살펴보도록 하겠습니다.

• 위 슬라이드의 7시 방향에 삼각형을 보면 \(cos\theta = \frac{adj}{\Vert \vec{a} \Vert}\) 임을 알 수 있습니다. (adj = adjacent)
  • 이 때 adj는 자주색으로 \(\vec{a}\)를 \(\vec{b}\)에 정사영 시켰을 때의 선분입니다.
  • 양변을 정리하면 \(adj = \Vert \vec{a} \Vert cos\theta\)가 됩니다.
  • 위 식을 \(\vec{a} \cdot \vec{b} = \Vert \vec{a} \Vert \ \Vert \vec{b} \Vert cos\theta\) 에 대입하면
    • \(\vec{a} \cdot \vec{b} = \Vert \vec{b} \Vert \ adj\)가 됩니다.
• 정리해 보면 내적의 크기는 벡터의 norm 값과 \(cos\theta\)에 비례하게 됩니다.
  • 여기서 \(cos\theta\) 값에 비례하는 것에 의미가 있습니다.
  • 두 벡터의 끼인 각 \(\theta\)에 따라서 \(cos\theta\)의 값은 0과 1사이 값을 가집니다.
  • 두 벡터의 방향이 겹치면 1, 직각이면 0의 값을 가집니다.
  • 즉, 내적을 이용하면 두 벡터가 얼마나 같은 방향을 가지는 지 알 수 있습니다.

• 내적과 동일한 방법으로 외적의 의미에 대하여 알아보도록 하겠습니다.
• 외적은 \(\Vert \vec{a} \times \vec{b} \Vert = \Vert \vec{a} \Vert \ \Vert \vec{b} \Vert sin\theta\) 이고
• 두 벡터 사이의 끼인각 \(\theta\)를 이용하면 \(sin\theta = \frac{opp}{\Vert \vec{a} \Vert}\) 이 됩니다. (opp = opposite)
  • 식을 정리하면 \(opp = \Vert \vec{a} \Vert sin\theta\) 가 되므로
  • 외적 \(\Vert \vec{a} \times \vec{b} \Vert = \Vert \vec{b} \Vert \ opp\) 가 됩니다.
• 위 식에서 \(sin\theta\)에 의미를 보면 \(\theta\)가 0일 때에는 0을 90일때는 1을 가집니다.
• 즉 두 벡터가 얼마나 orthogonal 한 지를 알 수 있습니다.

• 외적을 이용하면 평행사변형의 넓이 또한 쉽게 구할 수 있습니다.
• 위의 슬라이드 처럼 Area = \(\Vert \vec{b} \Vert \cdot\) height = \(\Vert \vec{b} \Vert \ \Vert \vec{a} \Vert sin\theta = \Vert \vec{a} \times \vec{b} \Vert\) 가 됩니다.
• 즉, 벡터의 외적은 두 벡터로 이루어진 평행사변형 넓이가 됩니다. (물론 3차원 공간상에서만 의미가 됩니다.)