벡터 삼중적의 확장

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

• 선형대수학 전체 글 목록

이번 글에서는 벡터 삼중적의 확장에 대하여 알아보도록 하겠습니다. 간단하게 말해서 세개의 3차워 벡터의 외적을 내적으로 변환하는 방법입니다.

• ·$\vec{a} \times (\vec{b} \times \vec{c}) = \vec{b}(\vec{a} \cdot \vec{c}) - \vec{c}(\vec{a} \cdot \vec{b})$입니다.
• 이번 강의에서는 위 식이 어떻게 유도되는지 알아보도록 하겠습니다.
• 변환 식을 이용하면 계산 복잡도를 줄일 수 있어서 유용합니다.

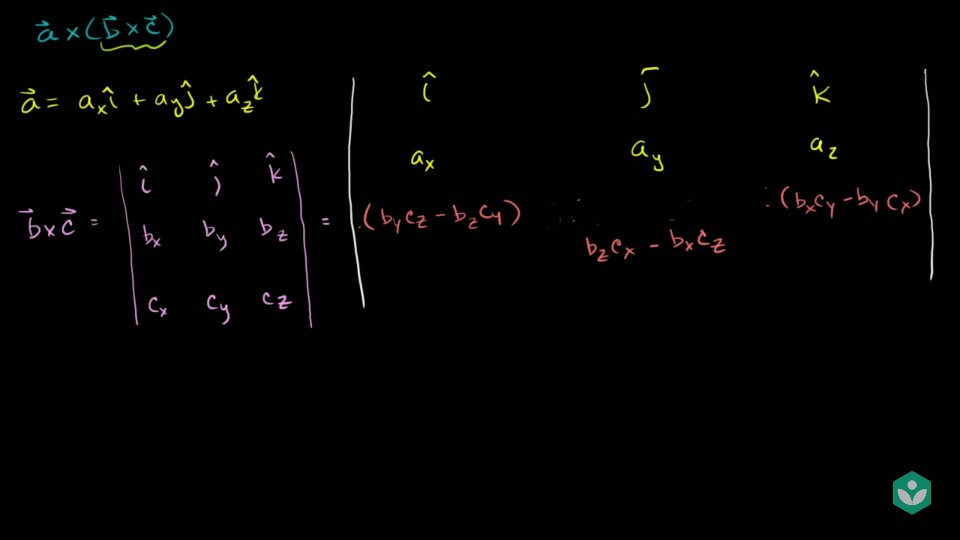
• 벡터의 외적 성질에 맞게 전개 합니다.
• 위의 슬라이드에서 $i, j, k$는 단위 벡터 입니다.
• ·$\vec{a} = [a_{x}, a_{y}, a_{z}], \vec{b} = [b_{x}, b_{y}, b_{z}], \vec{c} = [c_{x}, c_{y}, c_{z}]$ 입니다.
• 위 슬라이드의 보라색 식 전개는 $\vec{b} \times \vec{c}$ 이고 자주색 전개는 $\vec{a}$ 와 $\vec{b} \times \vec{c}$ 간의 외적 입니다.

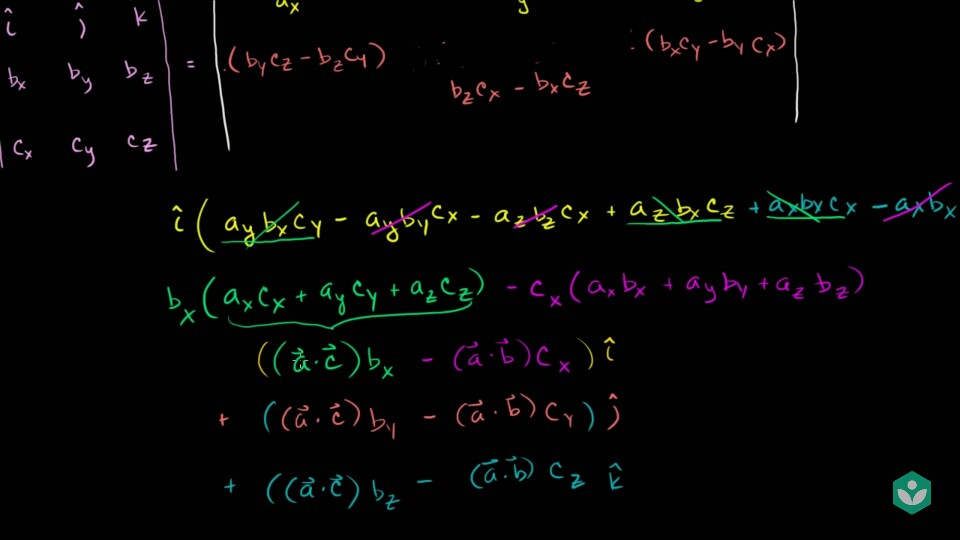
• ·$\vec{a} \times (\vec{b} \times \vec{c})$의 결과 또한 3차원 벡터입니다.
• 위 슬라이드와 같이 정리하면 벡터의 값은 다음과 같이 정리 됩니다.
  • ·$((\vec{a} \cdot \vec{c})b_{x} - (\vec{a} \cdot \vec{b})c_{x})\hat{i}$
  • ·$((\vec{a} \cdot \vec{c})b_{y} - (\vec{a} \cdot \vec{b})c_{y})\hat{j}$
  • ·$((\vec{a} \cdot \vec{c})b_{z} - (\vec{a} \cdot \vec{b})c_{z})\hat{k}$

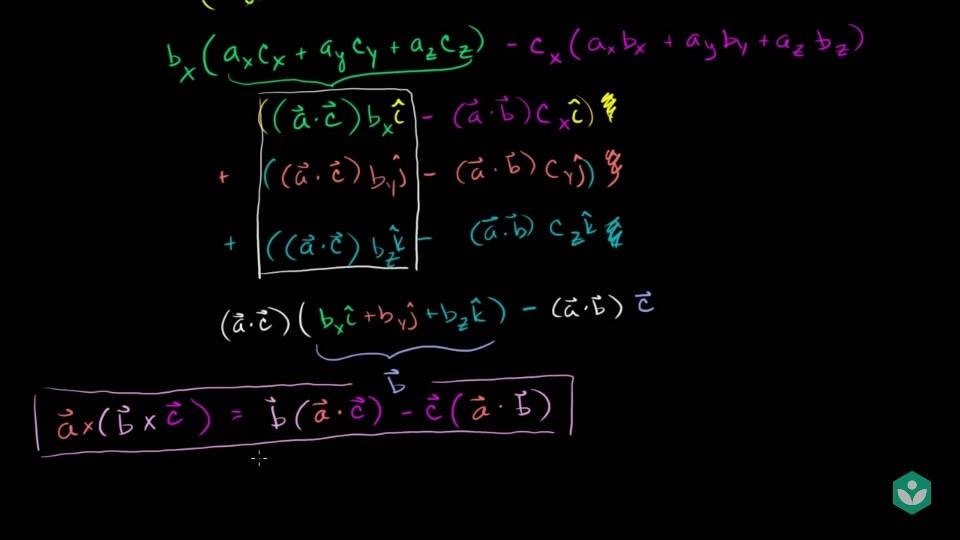
• 마지막으로 단위 벡터로 정리된 값들을 정리해 보면 다음과 같습니다.
  • ·$(\vec{a} \cdot \vec{c})(b_{x}\hat{i} + b_{y}\hat{j} + b_{z}\hat{k}) - (\vec{a} \cdot \vec{b})\vec{c}$
  • ·$b_{x}\hat{i} + b_{y}\hat{j} + b_{z}\hat{k} = \vec{b}$ 로 정리하면
  • ·$\vec{a} \times (\vec{b} \times \vec{c}) = \vec{b}(\vec{a} \cdot \vec{c}) - \vec{c}(\vec{a} \cdot \vec{b})$ 입니다.