부분공간의 기저 (Basis of Subspace)

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

이번 글에서는 subspace(부분공간)의 basis(기저)에 대하여 알아보도록 하겠습니다.

$Drawing$

이전 글에서 살펴 보았듯이 subspace를 이루기 위해서는 subspace를 구성하는 벡터들 끼리

위의 슬라이드 처럼 이런 조건의 subspace를 다음과 같이 나타낼 수 있습니다.

$V = span(\vec{v_{1}}, \vec{v_{2}}, ... , \vec{v_{n}}), \{\vec{v_{1}}, \vec{v_{2}}, ... , \vec{v_{n}} \}$ are linearly independent.

이 때, 벡터들이 subspace를 구성하기 위한 최소한의 subset일 때, 이 집합을 basis라고 합니다.
예를 들어 연두색 글씨를 보면 basis에 추가적으로 $\vec{v_{c}} = \vec{v_{1}} + \vec{v_{2}}$ 를 추가합니다.
- 이렇게 $\vec{v_{c}}$ 를 subset 으로 구성한 subspace를 T라고 하겠습니다.
- 이 때, span(T) = span(V) 이지만 #subset T > # subset V 이므로 subset T에는 불필요한 요소가 있습니다.
- 정리하면, subset T는 subspace를 구성할 수 있지만 최소한의 subset은 아닙니다.
- 즉, subset T는 덧셈 연산에 닫혀 있고 스칼라 곱에 닫혀 있지만, linealy dependent 합니다.
basis를 이용하여 subspace를 구성하면
- 덧셈 연산에 닫혀 있고
- 스칼라 곱에 닫혀 있고
- linearly independent 합니다.

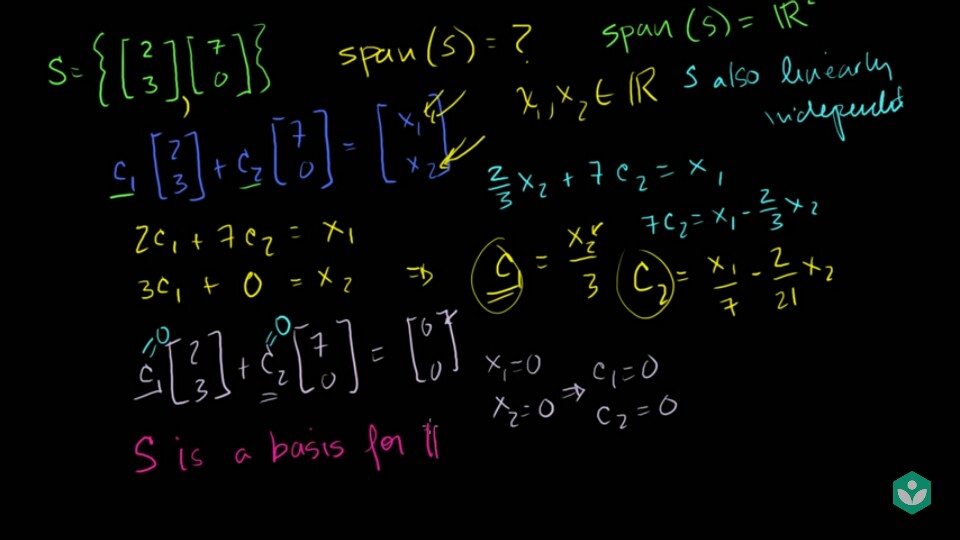
$Drawing$

예를 들어, $S = \{ [2, 3 ]^{T}, [7, 0]^{T}\}$ subset이 있다고 가정해 보겠습니다.

위의 슬라이드 처럼 식을 정의한 다음에 전개해 보면 $c_{1}, c_{2}$ 는 어떠한 실수 $x_{1}, x_{2}$가 들어왔을 때, 그 값에 따라 다양한 값들을 만들어 낼 수 있습니다.
특히 $x_{1} = 0, x_{2} = 0$ 일 때, $c_{1} = 0, c_{2} = 0$ 으로 유일한 해를 가지므로 linearly independent 합니다.

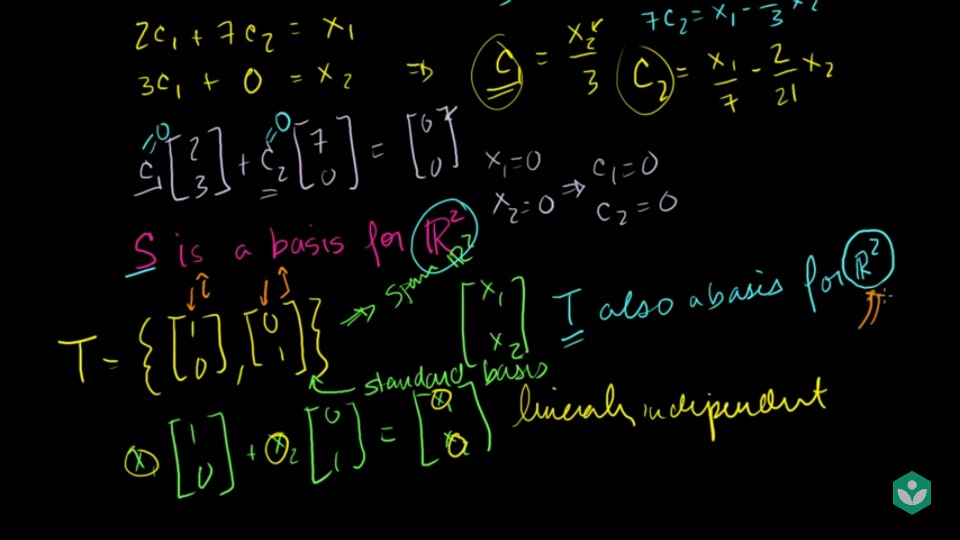
$Drawing$

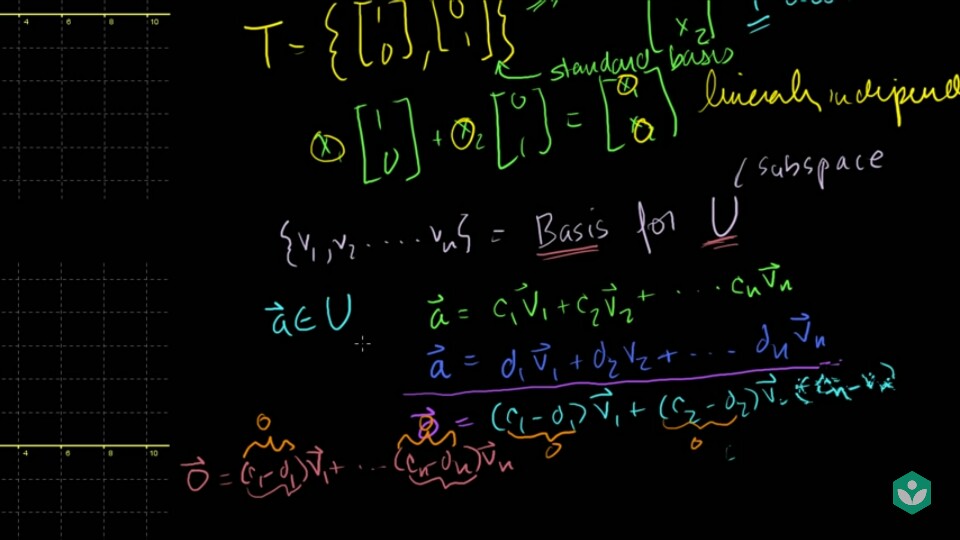
$Drawing$

이 때, 중요한 성질 중의 하나는 subspace의 각각의 원소를 basis의 결합으로 만들 때, 그 방법은 유일하다는 것입니다.
- 즉, basis를 이용하여 subspace의 어떤 원소를 만드는 방법은 1가지 입니다.
이것을 간단하게 증명해 보면 위 슬라이드와 같습니다.
basis인 $\{ \vec{v_{1}}, \vec{v_{2}}, ... , \vec{v_{n}} \}$의 결합으로 만들어진 $\vec{a}$ 가 있다고 가정합시다.
만약 $\vec{a} = c_{1}\vec{v_{1}} + c_{2}\vec{v_{2}} + ... + c_{v_{n}}\vec{n}$ 으로 만들어 질 때, 또 다른 결합으로 만들어 질 수 있다면 basis는 유일하지 않습니다.
만약, 또 다른 결합 $\vec{a} = d_{1}\vec{v_{1}} + d_{2}\vec{v_{2}} + ... + d_{n}\vec{v_{n}}$ 이 존재한다고 가정해 보겠습니다.
위 슬라이드 처럼, 두 식을 빼서 정리한 식을 보면 각각의 항은 $(c_{i} - d_{i})\vec{v_{i}}$ 로 정리가 됩니다.
basis의 정의에 따라 linear independent 하므로 $c_{i} - d_{i} = 0$ 을 만족해야 합니다.
- 즉, $c_{i} = d_{i}$ 가 되어 어떤 원소를 만드는 basis의 조합은 1가지 임을 알 수 있습니다.