벡터 사이의 각 정의하기

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

이번 글에서는 벡터 사이의 각을 정의하는 방법에 대하여 알아보겠습니다.

$Drawing$

위 슬라이드를 보면 3개의 벡터로 이루어진 삼각형 모양을 벡터의 길이를 이용하여 삼각형과 그 변의 길이로 표현하였습니다.
이 때, $\Vert \vec{x} + \vec{y} \Vert \le \Vert \vec{x} \Vert + \Vert \vec{y} \Vert$ 식을 이용하면 위의 슬라이드 처럼 삼각형의 변의 관계를 나타낼 수 있습니다.
- 각각, $\Vert \vec{a} \Vert$, $\Vert \vec{b} \Vert$, $\Vert \vec{a} - \vec{b} \Vert$ 를 변경해서 식을 증명 하였습니다.

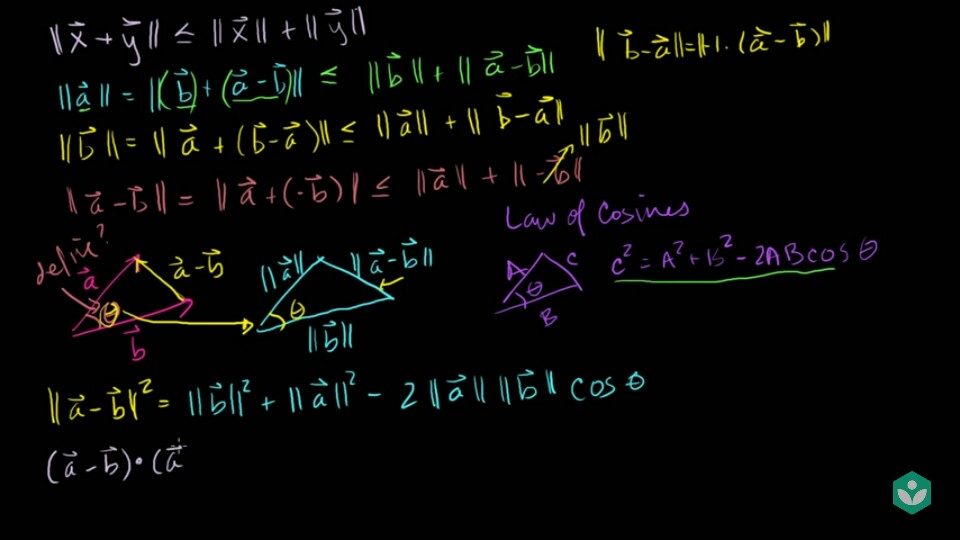
$Drawing$

위 슬라이드를 보면 3개의 벡터로 이루어진 삼각형에서 $\vec{a}$ 와 $\vec{b}$ 사이의 끼인각은 어떻게 표현할 수 있을까요?
코사인 법칙을 이용하면 사이의 끼인 각을 알 수 있습니다.
- 코사인 법칙은 세 변의 길이를 알면 대각선과 마주보는 각의 크기를 알 수 있습니다.

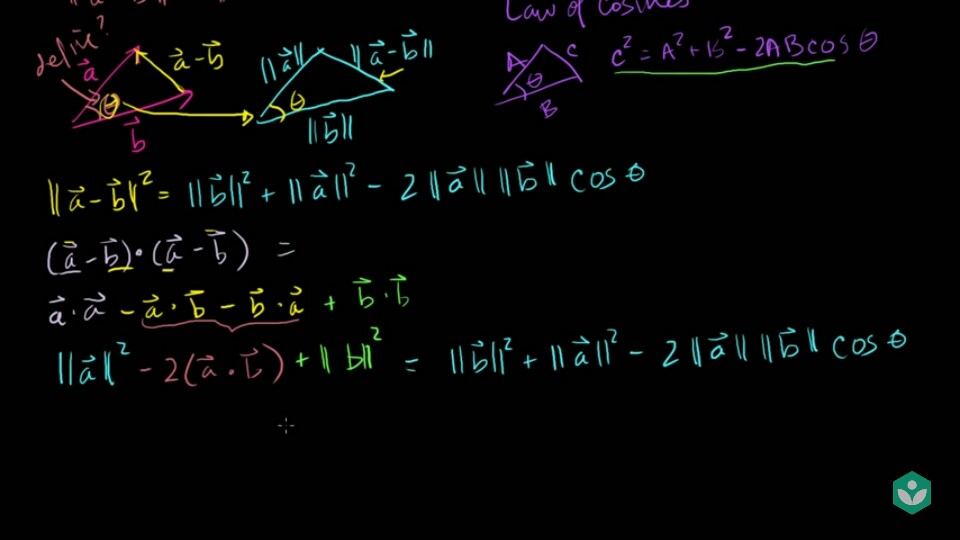
$Drawing$

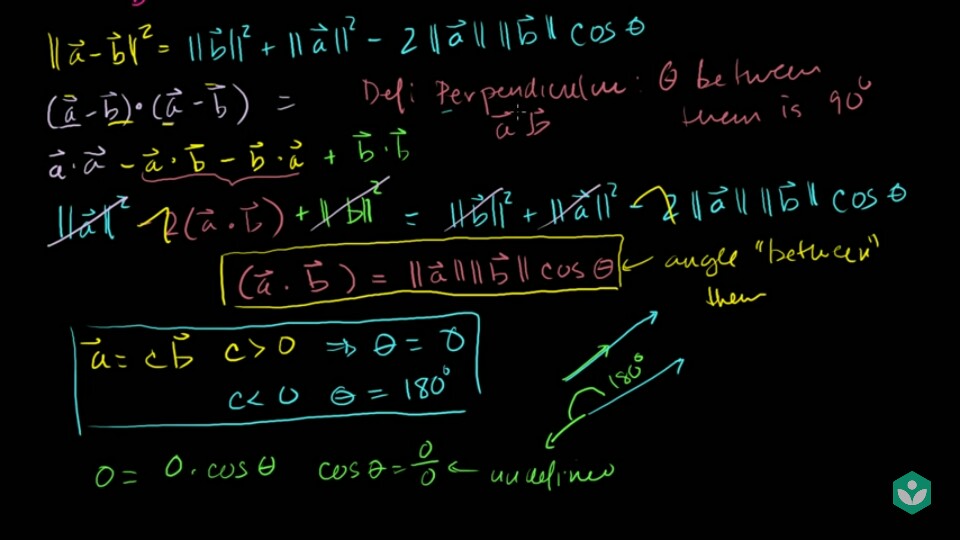
$Drawing$

식을 최종적으로 정리를 하면 $\vec{a} \cdot \vec{b} = \Vert \vec{a} \Vert \Vert \vec{b} \Vert cos \theta$ 가 됩니다.
- 이 때 $\theta$ 가 벡터 사이의 끼인 각이 됩니다.
우리가 구하는 끼인각은 $\vec{a}$ 와 $\vec{b}$ 사이의 각입니다.
만약 $\vec{a} = c \vec{b}$ 관계를 가진다면 벡터가 같은 위치에 있으므로 각 $\theta$는 0도 또는 180도를 가지게 됩니다.
- 코사인 값의 분포에 따르면 c > 0 일 때에는 $\theta = 0$ 이고 c < 0 이면 $\theta = 180$이 됩니다.
마지막으로 정리하면 $cos\theta = \frac{\vec{a} \cdot \vec{b}}{\Vert \vec{a} \Vert \Vert \vec{b} \Vert}$ 로 유명한 코사인 유사도, Cosine Similarity가 됩니다.

$Drawing$

이 때 헷갈릴 수 있는 용어가 있습니다. 직각(perpendicular)과 직교(orthogonal) 입니다.
이 용어를 정의하기 전에 두 벡터의 내적이 0이면 항상 $cos \theta$ 에서 $\theta = 90$ 일 까요?
- 아닙니다. 왜냐하면 0벡터가 존재할 수 있기 때문입니다.
따라서 영벡터의 존재 유무가 정의되지 않은 상태에서는 두 벡터 사이의 각이 90도라고 단정지을 수 없습니다.
이 때, $\vec{a}$ 와 $\vec{b}$ 가 직각이라면 두 벡터의 내적은 0이 성립합니다.
- 반면 두 벡터의 내적이 0이라도 $\vec{a}$ 와 $\vec{b}$ 가 직각이라고는 할 수 없습니다. (영벡터 때문입니다.)
반면, $\vec{a} \cdot \vec{b} = 0$ 이면 직교(orthogonal) 한다고 말합니다.
따라서 직교 + 영벡터가 없음 = 직각 이라고 할 수 있습니다.