벡터 내적의 성질 증명

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

• 선형대수학 전체 글 목록

이번 글에서 배울 내용은 벡터 내적의 3가지 성질 입니다.

• 벡터의 내적은 교환 법칙이 성립한다.
• 벡터의 내적은 벡터 합에 대한 결합 법칙이 성립한다.
• 벡터의 내적은 스칼라 곱에 대한 결합 법칙이 성립 한다.

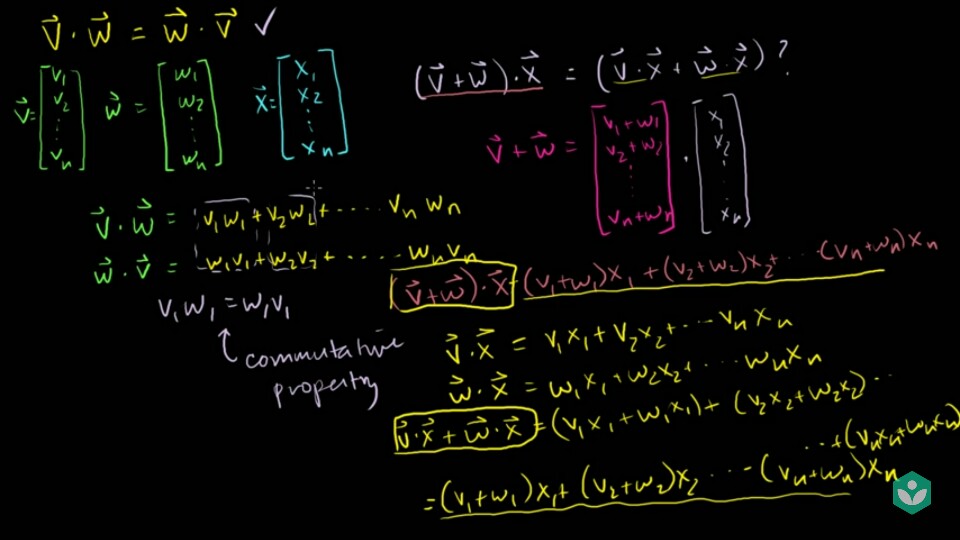
• 벡터의 내적은 교환 법칙이 성립한다.
  • 슬라이드 왼쪽을 보면 \(\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}\) 이 성립함을 알 수 있습니다.
• 벡터의 내적은 벡터 합에 대한 결합 법칙이 성립한다.
  • 슬라이드 오른쪽을 보면 \((\vec{v} + \vec{w}) \cdot \vec{x} = \vec{v} \cdot \vec{x} + \vec{w} \cdot \vec{x}\) 이 성립함을 알 수 있습니다.

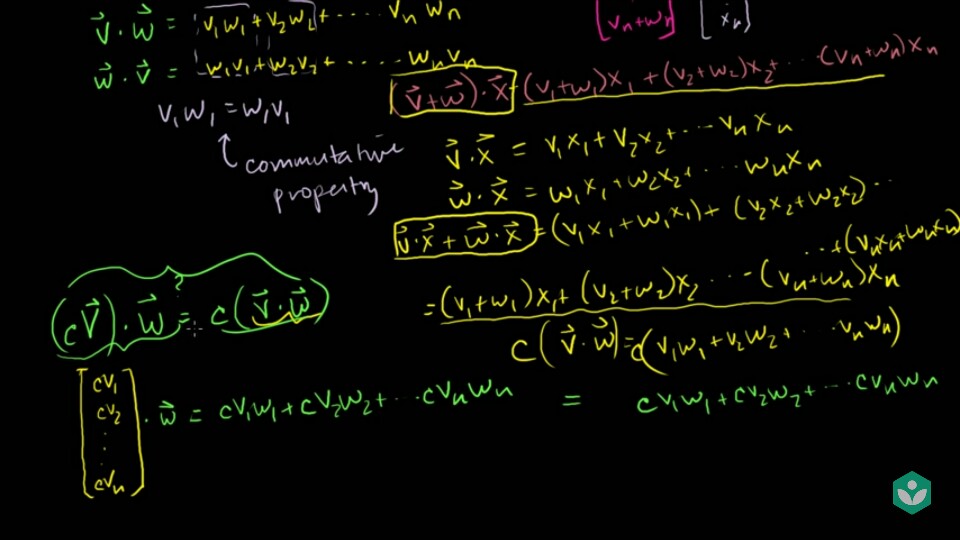
• 벡터의 내적은 스칼라 곱에 대한 결합 법칙이 성립 한다.
  • 슬라이드를 보면 \((c \vec{v}) \cdot \vec{w} = c(\vec{v} \cdot \vec{w})\) 이 성립함을 알 수 있습니다.