gram schmidt process

이번 글에서는 그램 슈미트 과정(gram schmidt process)에 대하여 알아보도록 하겠습니다.
그램 슈미트 과정은 orthonormal basis vector set을 구하는 과정입니다.
즉, 주어진 벡터들을 이용해서 서로 수직인 벡터들을 만드는 방법이라고 생각 할 수 있고 주어진 벡터들에 대한 직교기저(orthogonal basis) 또는 정규직교기저(orthonormal basis)를 구하는 과정이라고 생각하면 됩니다.
- 먼저 그램 슈미트 과정을 시작하기에 앞서 linearly independent한 벡터들이 있다고 가정해 보겠습니다. 예를 들어 $v_{1}, v_{2}, v_{3}$ 입니다.
자, 그러면 그램 슈미트 직교화 가정에 대하여 알아보도록 하겠습니다.

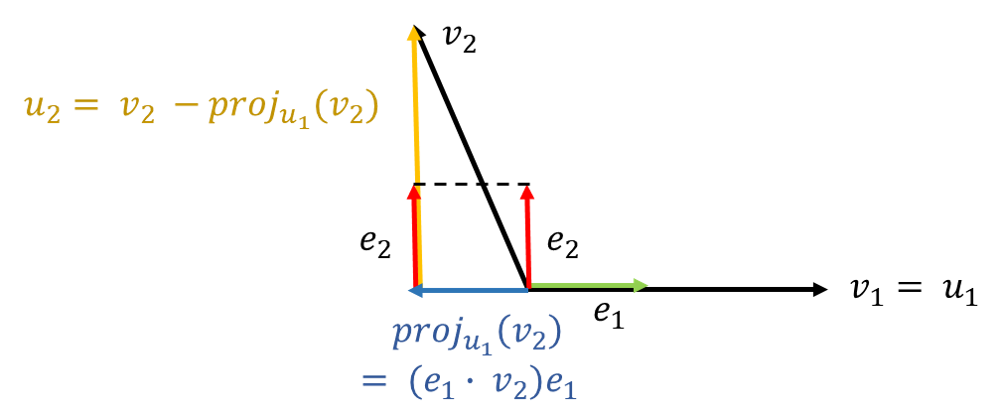
$Drawing$

먼저 벡터 $v_{1}$ 에서 부터 시작해 보겠습니다. $v_{1}$ 에 정규화를 해주면 $e_{1} = \frac{v_{1}}{\vert v_{1} \vert}$ 를 구할 수 있습니다.
그리고 뒤에서 계속 구할 $u_{i}$ 에서 $v_{1} = u_{1}$ 이라고 가정하겠습니다.
먼저 $v_{2}$ 에서 $v_{1}$ 으로 내린 projection을 이용하면 $v_{2}$ 를 다른 식으로 표현할 수 있습니다.
즉, $v_{2} = (v_{2} \cdot e_{1})e_{1} + u_{2}$ 가 됩니다. 여기서 $u_{2}$ 는 projection입니다.
다시 이 값을 정리하면 $u_{2} = v_{2} - (v_{2} \cdot e_{1})e_{1}$ 가 됩니다.
그리고 $u_{2}$ 에 정규화를 해주게 되면 $e_{2} = \frac{ u_{2} }{ \vert u_{2} \vert }$ 로 정의 할 수 있습니다.
지금 까지 한 것을 보면 비교해야 할 대상은 e1,e2 입니다. 이 두 벡터는 서로 orthonormal한 관계를 가집니다.
- 즉, 두 벡터는 서로 직교하고 벡터의 크기는 1입니다.
위와 같이 어떤 벡터가 있을 때, 그 벡터와 수직인 벡터를 만드는 과정을 그람 슈미트 과정이라고 합니다.
이 과정은 벡터가 추가되어도 추가된 벡터와 이전 벡터들 모두에 직교하는 벡터들을 만들 수 있습니다.

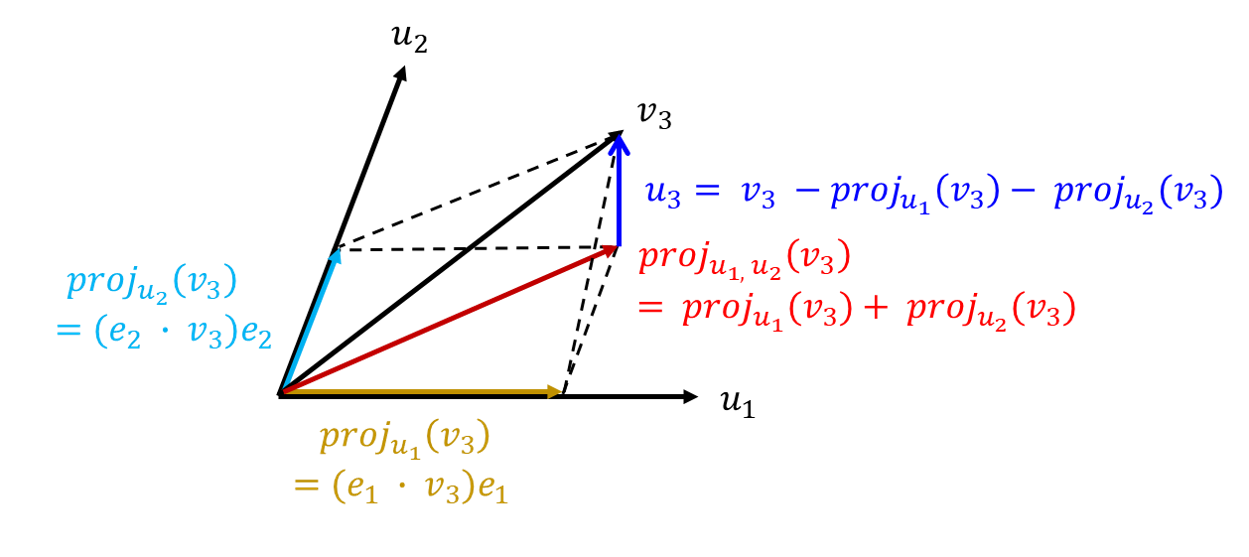
$Drawing$

앞의 예제에서는 $v_{2}$ 벡터와 $u_{1}$ 벡터를 이용하여 서로 직교인 벡터인 $u_{1}, u_{2}$ 를 구하였습니다.
이번에는 $v_{3}$ 라는 벡터를 하나 더 추가하여 모두 직교 관계를 가지는 벡터 3개를 만들려고 합니다.
앞에서 구한 $u_{1}, u_{2}$ 벡터를 이용해 보겠습니다. 현재 $u_{1}, u_{2}$ 는 직교인 상태 입니다.
이 때, u1,u2를 이용하여 빨간색 벡터를 만들면 빨간색 벡터와 u3라는 파란색 벡터를 이용하여 v3 벡터를 구할 수 있습니다.
- 즉, $u_{3} = v_{3} - proj_{u_{1}}(v_{3}) - proj_{u_{2}}(v_{3})$ 가 됩니다.
이 때 그한 벡터 $u_{3}$ 를 정규화 해주면 $e_{3} = \frac{ u_{3} }{ \vert u_{3} \vert }$ 를 구할 수 있습니다.

위 관계를 확장해 보면 $u_{n} = v_{n} - proj_{ u_{1} }(v_{n}) - proj_{ u_{2} }(v_{n}) - \cdots - proj_{u_{n-1}}(v_{n}) = v_{n} - \sum_{i=1}^{n-1}proj_{u_{i}}(v_{n})$ 이 됩니다.

여기서 주목할 점은, 직교한 벡터도 아니고 유닛 벡터도 아닌 벡터들을 이용하여 정규 직교 벡터를 구하였다는 것입니다. 상당히 의미 있는 일입니다.
- 즉 N개의 선형 독립인 벡터를 이용하여 N개의 정규직교벡터를 구한 것입니다.
이 정규직교벡터는 특히 transformation을 할 때 사용되는데요, 그 응용에 대해서는 이후에 살펴보겠습니다.