Least Squares (최소 제곱법/자승법)
2016, Dec 01
- 이번 글에서는
Least Squares에 대하여 간략하게 알아보도록 하겠습니다. Least Squares는 \(Ax = b\) 의 행렬식에서 \(x\) 의 값을 찾고자 하는 것이며 정확한 해가 없다고 하더라도 근사값을 추정해줍니다.
목차
Least Squares의 목적

- 위 그림과 같이 (N, M) 크기의 행렬이 있다고 가정해 보겠습니다. 그러면 \(\text{rank}(A) = M\)을 만족합니다.
- 행렬 \(A\) 의
column space의 경우 \(N\) 차원 안에서 \(M\) 차원으로span하게 됩니다.
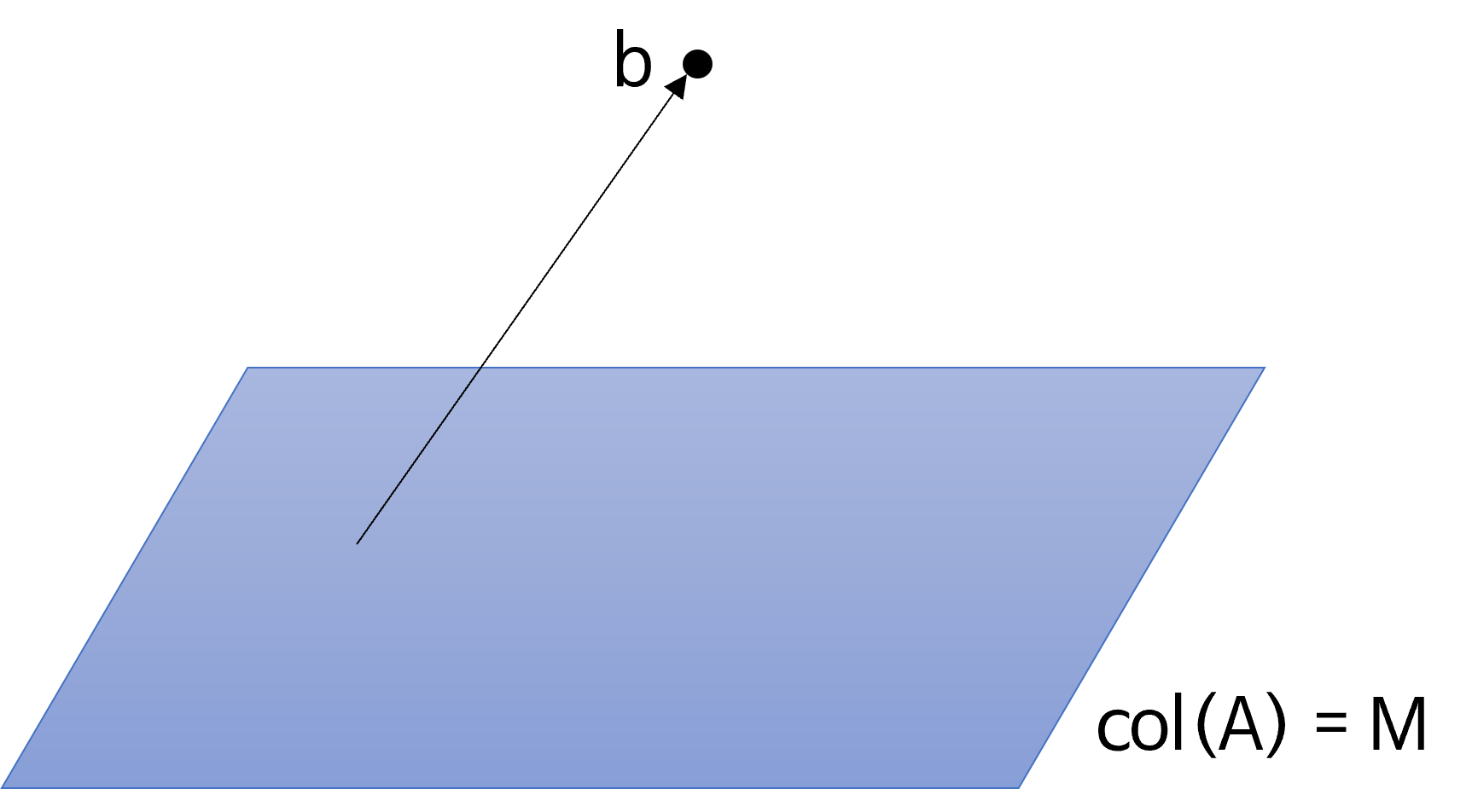
- 위 공간은 \(N\) 차원 공간 안에서 행렬 \(A\) 가
span하는 \(M\) 차원 공간을 의미합니다. - 이 때, \(N\) 차원 공간의 벡터 \(b\) 가 있다고 가정하겠습니다.
- 위 그림과 같이 \(b\) 는 \(M\) 차원
span공간 내부에 있지 않기 때문에 임의의 벡터 \(x\) 를 이용하여 표현한 \(Ax\) 로는 \(b\) 를 표현할 수 없고 흔히 이런 경우 해가 없다라고 말합니다. - 하지만 여기서 더 나아가 해가 없더라도 \(Ax\) 를 가능한한 \(b\) 에 가깝도록 만들어 보자는 문제로 변환하면 이 문제를 해결하는 방법이 여러가지가 있는데 그 중 하나가
Least Squares가 됩니다.
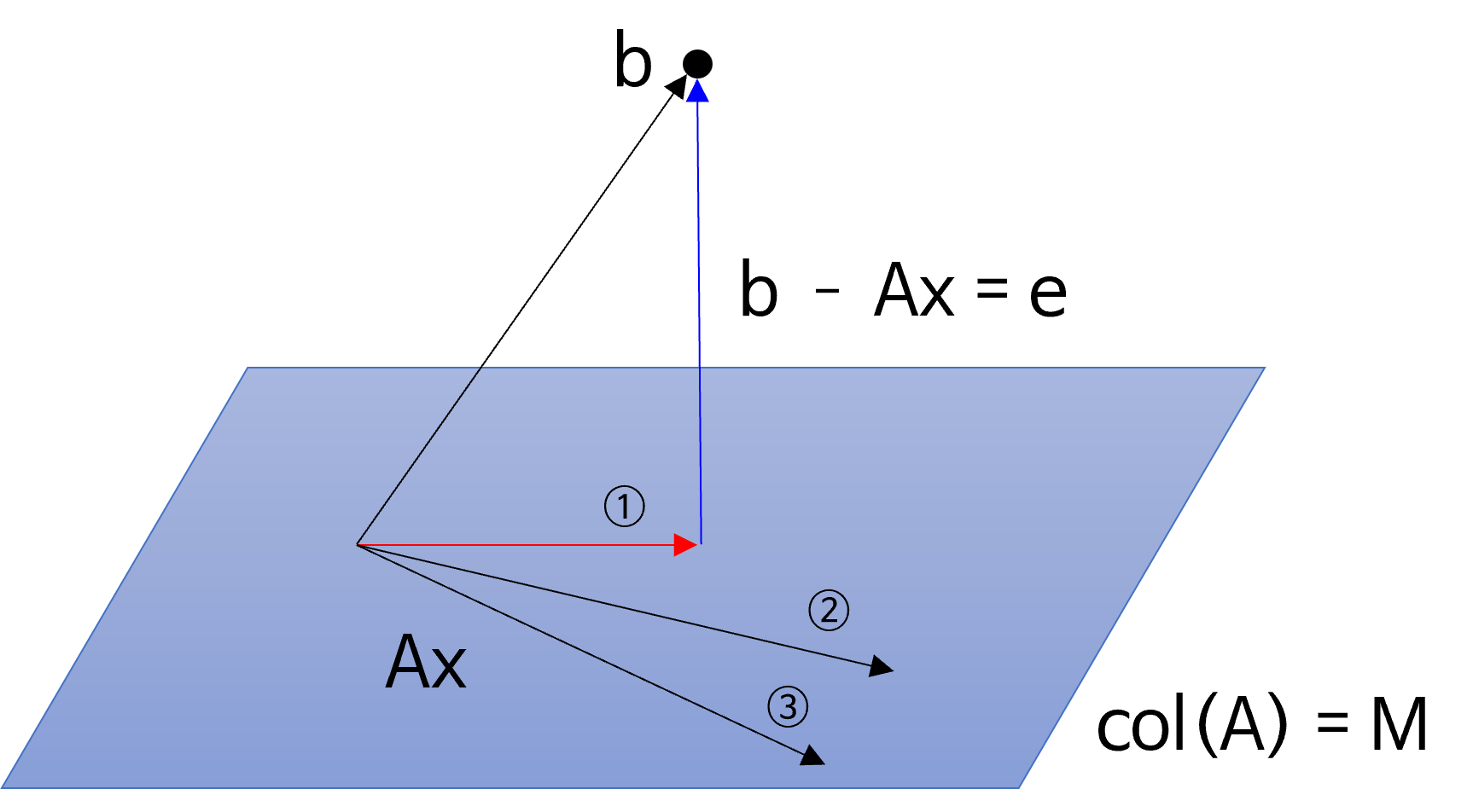
- 위 그림의
span공간에서 \(Ax\) 는 무수히 많은 경우의 수가 있지만 \(b - Ax\) 가 가장 작아지는 경우는 하나 존재하며 이 차이를 \(e = \text{error}\) 라고 정의하겠습니다. - 위 그림 예시에서는 ①이 가장
error가 작은 \(Ax\) 가 되며 이 값은 벡터 \(b\) 가span공간 상에projection하였을 때가 됩니다. - 즉 벡터 \(e\) 가 가장 작아지도록 하는 \(x\) 를 찾는 것이 목적입니다.
Least Squares는 이error를 정의할 때L2 Norm을 이용하여error를 정의하고 이error를 최소화 하고자 하는 방법을 사용합니다. 따라서error를 최소화 하는 것에서Least라는 용어를 사용하고error를 정의 하는 방법이L2 Norm이기 때문에Squares라는 용어를 사용하여Least Squares라고 불리게 됩니다.
- 정리하면
error제곱의 합을 최소화 하면 \(Ax = b\) 에 가장 근사한 \(x\) 를 찾을 수 있다는 알고리즘이Least Squares가 됩니다.
Least Squares의 풀이법
- 앞의 내용에서 ① 과 같은 벡터 \(Ax\) 를 찾으려면 \(Ax\) 와 \(e = b - Ax\) 가 직교해야 함을 기하학적으로 확인하였습니다.
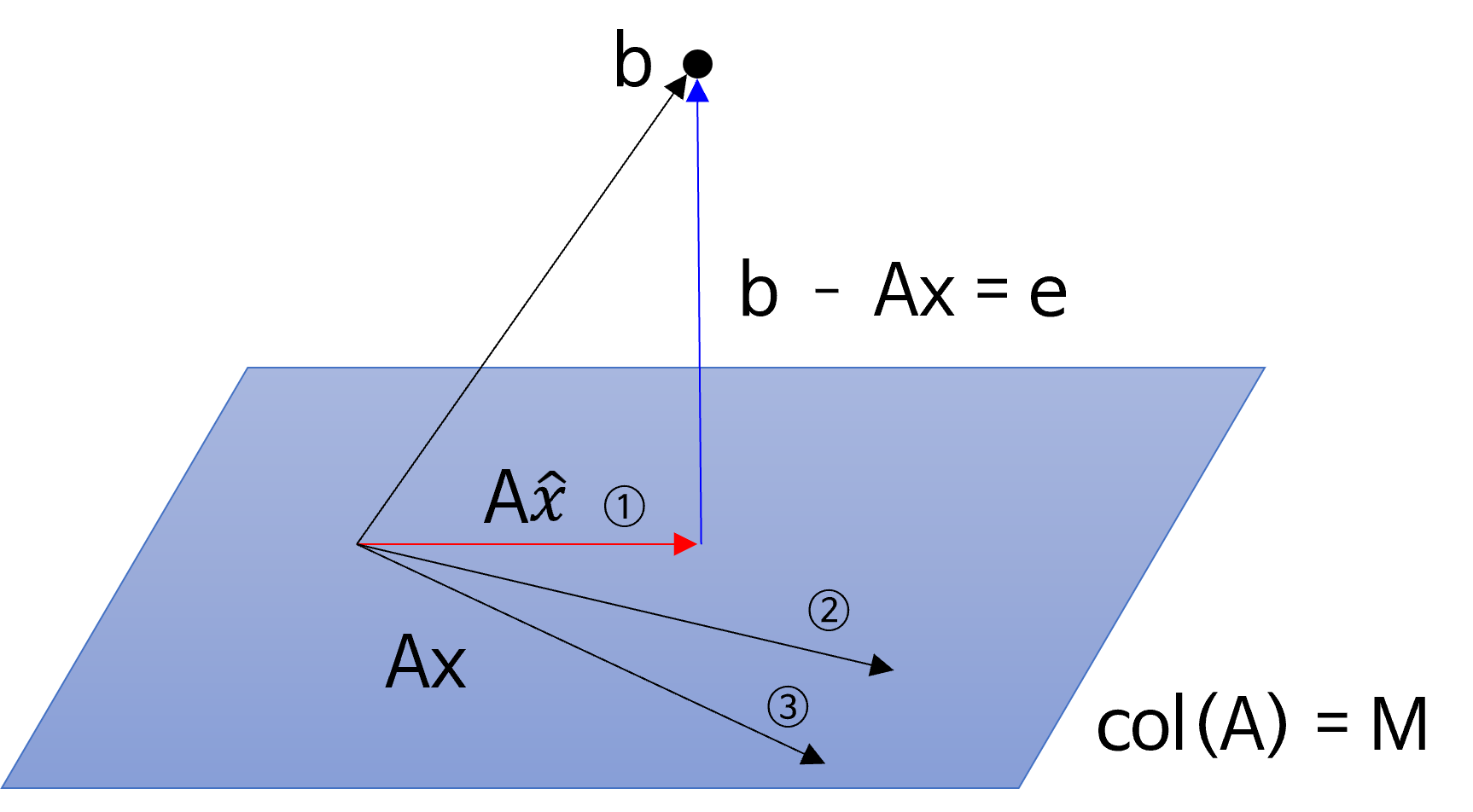
- 따라서 위 그림과 같이 \(A\hat{x}\) 의 \(\hat{x}\) 를 찾아보도록 하겠습니다. 두 벡터가 직교하려면 내적이 0이되면 되므로 다음과 같이 수식을 정의할 수 있습니다.
- \[(b - A\hat{x})^{T} A\hat{x} = 0 \tag{1}\]
- 식을 정리하여 \(\hat{x}\) 를 구할 수 있도록 식을 변형해 보겠습니다.
- \[(b^{T} - \hat{x}^{T}A^{T})A\hat{x} = 0 \tag{2}\]
- \[(b^{T}A - \hat{x}^{T}A^{T}A)\hat{x} = 0 \tag{3}\]
- 위 식의 좌변에서 \((b^{T}A - \hat{x}^{T}A^{T}A) = 0\) 이 되는 조건에서 \(\hat{x}\) 를 찾을 수 있습니다.
- \[b^{T}A - \hat{x}^{T}A^{T}A = 0 \tag{4}\]
- \[b^{T}A = \hat{x}^{T}A^{T}A \tag{5}\]
- 식 (5)의 양변에 Transpose를 적용하면 다음과 같습니다.
- \[A^{T}b = A^{T}A\hat{x} \tag{6}\]
- 식 (6)을
normal equation이라고 부릅니다. 위 식에서 \(A^{T}A\) 를 살펴보면 (M, N) 행렬과 (N, M) 의 곱으로 (M, M) 크기의 행렬이 됩니다. 따라서 \(\text{rank}(A^{T}A) = \text{rank}(A) = M\) 이 되며 역행렬을 가집니다. 식 (6)을 정리하면 다음과 같습니다. - 만약 \(A\) 의
rank가 full-rank가 아니라면pseudo-inverse를 이용하여inverse를 구할 수 있으며 아래 링크에서 관련 내용을 살펴보시면 됩니다.Singular Value Decomposition: https://gaussian37.github.io/math-la-svd/
- \[\hat{x} = (A^{T}A)^{-1}A^{T}b \tag{7}\]
- 따라서 식 (7)과 같이
(N, M)크기의 행렬 \(A\) 와N차원의 벡터 \(b\) 를 이용하면M차원의 벡터 \(\hat{x}\) 를 유도할 수 있습니다. 여기까지가Least Squares의 핵심 내용입니다. M차원의 벡터 \(\hat{x}\) 는 \(A\hat{x}\) 를 가장 \(b\) 와 유사하도록 만들어주는 벡터이므로 선형 모델의 파라미터를 추정할 때, \(\hat{x}\) 를 추정함으로써 파라미터를 찾는 방법을 많이 사용합니다. 이와 관련된 내용은 실습 부분에서 살펴보도록 하겠습니다.
- 식 (7)의 양변에 \(A\) 를 곱하면 다음과 같습니다.
- \[A\hat{x} = A(A^{T}A)^{-1}A^{T}b \tag{8}\]
- \[A\hat{x} = P_{A} b \tag{8}\]
- 식 (7)의 \(A(A^{T}A)^{-1}A^{T} = P_{A}\) 로 표현할 수 있습니다. 왜냐하면 \(P_{A}\) 를 \(b\) 에 곱함으로써 \(A\hat{x}\) 를 구할 수 있고 \(A\hat{x}\) 가 벡터 \(b\) 를 \(A\) 공간에
projection한 결과이기 때문입니다.
Least Squares의 사용 예시
Least Squares를 사용하는 흔한 예시는 관측값에noise가 추가된 경우noise가 없는 값을 추정하고자 하는 경우입니다.
- \[z = Ax + n\]
- 위 식에서 \(z\) 를 관측값, \(A\) 는 모델링 관련 행렬, \(x\) 는 입력 벡터, \(n\) 은 노이즈라고 정의 하겠습니다.
- 실제 원하는 관측값 \(z = Ax\) 을 필요로 하지만 관측하는 대부분의 경우 노이즈 \(n\) 이 추가가 됩니다.
- 이 때, \(n\) 이 랜덤한 노이즈로 추가되기 때문에 \(Ax\) 공간에 표현할 수 없고 외부의 공간에 \(z\) 값이 형성되기 때문에 \(A\hat{x}\) 를 추정해야 합니다.
Least Squares의 Numpy 구현
import numpy as np
import matplotlib.pyplot as plt
f = np.poly1d([5, 1])
# x : (30, )
x = np.linspace(0, 10, 30)
# b : (30, )
b = f(x) + 10*np.random.normal(size=len(x))
xn = np.linspace(0, 10, 200)
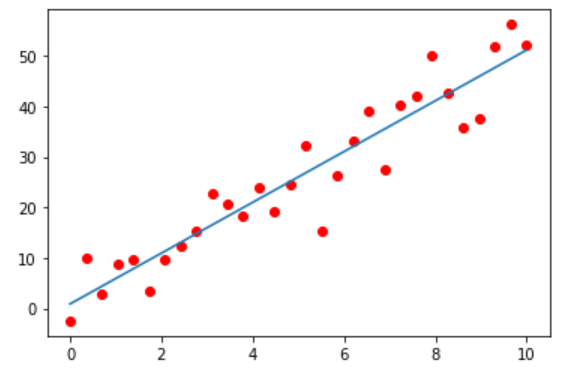
plt.plot(x, b, 'or')
plt.show()
# 값이 1인 열은 선형 회귀 모델에서 절편의 추정하도록 하며 다른 값으로 바꿀 수도 있습니다.
A = np.vstack([x, np.ones(len(x))]).T
m, c = np.matmul(np.linalg.inv(np.matmul(A.T, A)), np.matmul(A.T, b))
print(m, c)
# 5.033542358928728 1.7561754039237234
yn = np.polyval([m, c], xn)
plt.plot(x, y, 'or')
plt.plot(xn, yn)
plt.show()