matrices transform into the new basis vector set

이번 글에서는 어떤 좌표계에서 basis였던 벡터들을 다른 좌표계로 변환시키는 방법에 대하여 배워보려고 합니다.
자 그러면 2차원의 2개의 basis 벡터를 어떻게 새로운 좌표계로 변환시키는 지 알아보겠습니다.

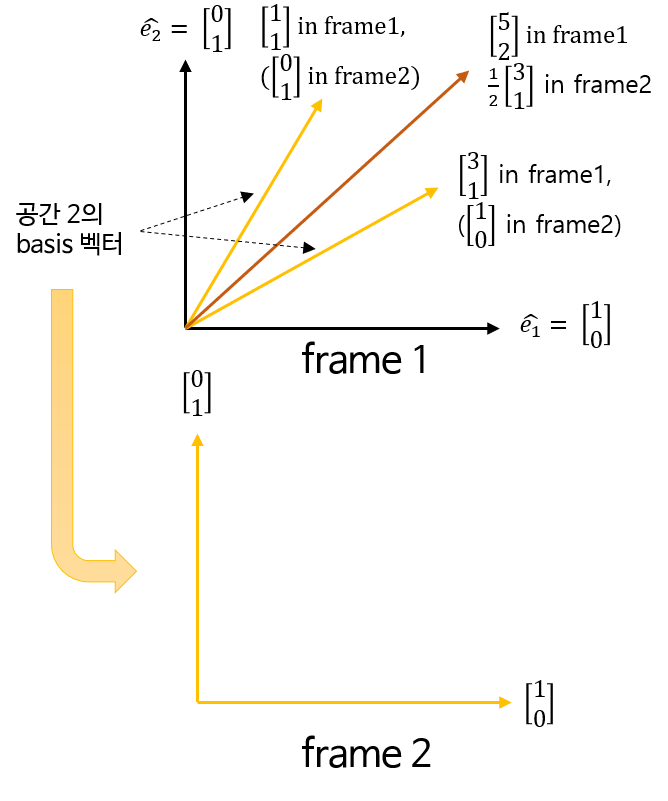
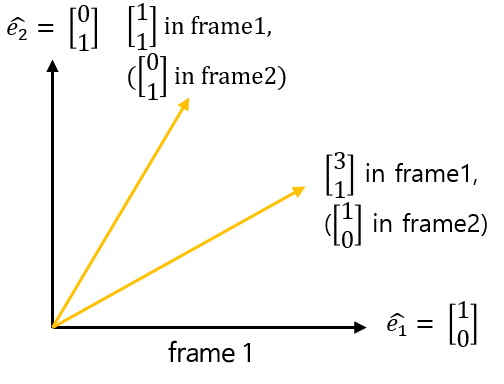
$Drawing$

만약 2개의 frame이 있다고 가정해 보겠습니다. 현재 그래프에서 사용하고 있는 frame1은 basis 벡터가 $\hat{e_{1}}, \hat{e_{2}}$로 이루어진 공간입니다.
- 검은색 화살표로 이루어진 축입니다.
frame1에서 노란색으로 칠해진 벡터는 frame2의 basis 벡터입니다.
frame2의 basis 벡터는 frame2에서는 유닛 벡터 형태의 basis 벡터이지만 frame1에서 표현될 때는 변형 되어서 $[1, 1]^{T}, [3, 1]^{T}$로 표현됩니다.
그러면 frame1과 frame2 각각의 basis 벡터에 대하여 알고 있고 frame2의 basis 벡터가 frame1에 어떻게 표현되는 지 알고 있으므로 frame2의 모든 벡터를 frame1에 표현할 수 있습니다.

위 그래프의 갈색 벡터를 보면 frame2에서는 $\frac{1}{2}[3, 1]^{T}$ 였습니다
이 벡터가 frame1에서는 어떻게 나타날 수 있을까요? 이 때, 필요한 개념이 transformation 입니다.
연산하는 방법은 다음과 같습니다.

[\begin{bmatrix} 3 & 1 \ 1 & 1 \ \end{bmatrix} \begin{bmatrix} \frac{3}{2} \ \frac{1}{2} \ \end{bmatrix} = \begin{bmatrix} 5 \ 2 \ \end{bmatrix}]

이 때, 첫번째 행렬인 $\begin{bmatrix} 3 & 1 \\ 1 & 1 \\ \end{bmatrix}$ 은 frame1 상에서의 fram2의 basis 벡터에 해당합니다.
- 이 행렬을 transformation matirx라고 합니다.
두번째 항인 벡터 $\begin{bmatrix} \frac{3}{2} \\ \frac{1}{2} \\ \end{bmatrix}$는 frame2 상에서의 벡터입니다.
첫번째 항인 행렬과 두번째 항인 벡터의 곱은 변형된 frame1상에서의 frame2 벡터가 됩니다.
따라서 연산 과정을 정리하면 frame1 vector = transformation matrix * frame2 vector

그러면 반대로 frame1상에서의 벡터를 frame2에서 표현할 수 있도록 변형하려면 어떻게 하면 될까요?
방법은 간단합니다. 앞에서 구한 transformation matrix의 역행렬을 이용하여 구할 수 있습니다.
즉, fram2 vector = inverse of transformation matrix * frame1 vector 가 됩니다.
따라서 역행렬인 $\begin{bmatrix} 1 & -1 \\ -1 & 3 \\ \end{bmatrix}$ 가 frame1 → frame2로의 transformation matrix가 됩니다.

이번에는 다른 예제를 한번 살펴보도록 하겠습니다.

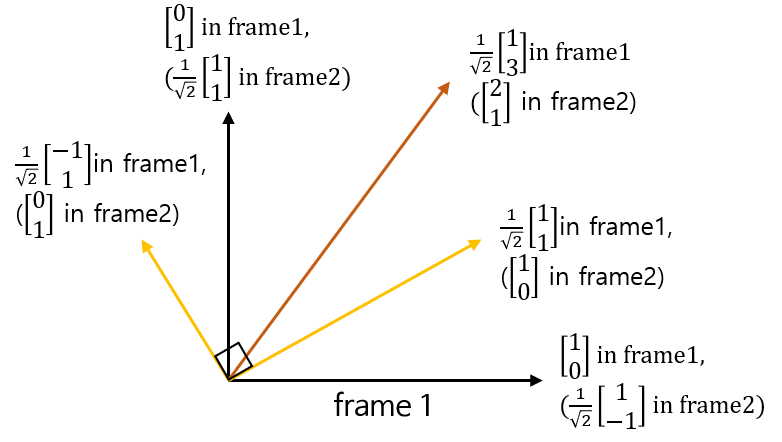
$Drawing$

앞의 예제와 같이 frame1과 frame2간의 transformation matrix를 만들면 다음과 같습니다.
- frame2 → frame1 : $B = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \\ \end{bmatrix}$
- frame1 → frame2 : $B^{-1} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ -1 & 1 \\ \end{bmatrix}$
따라서 $B * [2, 1]^{T} = \frac{1}{\sqrt{2}}[1, 3]^{T}$ 가 되고 $B^{-1} * \frac{1}{\sqrt{2}}[1, 3]^{T} = [2, 1]^{T}$가 됩니다.
이번 예제를 보면 앞의 예제와 다른점이 하나 있습니다. frame1에 표현된 frame2에서의 basis 벡터가 frame1에서 서로 직교합니다. (노란색 벡터들)
이 경우에 벡터를 변환 할 때 좀 더 편하게 할 수 있습니다.
변환할 벡터와 basis 벡터를 각각 곱해주면 basis에 해당하는 성분을 구할 수 있습니다.
- 예를 들면 $\frac{1}{\sqrt{2}}[1, 3]^{T}$ 을 frame2에서의 벡터값을 구하고 싶으면
- 먼저 $\frac{1}{\sqrt{2}}[1, 3]^{T} * \frac{1}{\sqrt{2}}[1, 1]^{T} = 2$ 를 구할 수 있고
- 다음으로 $\frac{1}{\sqrt{2}}[1, 3]^{T} * \frac{1}{\sqrt{2}}[-1, 1]^{T} = 1$을 구할 수 있습니다.
- 각 basis 성분에 해당하는 값을 구할 수 있고 transformation matrix를 이용하여 연산한 것과 같이 $[2, 1]^{T}$를 구할 수 있습니다.
이 성질은 basis 벡터에 해당하는 두 벡터가 서로 직교할 때만 가능하므로 직교 관계인 것만 알 수 있으면 계산을 좀 더 편리하게 할 수 있습니다.

만약 frame1에서 어떤 벡터의 변환이 발생하였을 frame2에서도 반영되게 하려면 어떻게 처리해야 할까요?
예를 들어 frame1에 회전 변환이 발생하였을 때, frame2의 벡터는 어떻게 변환되는지 살펴보겠습니다.

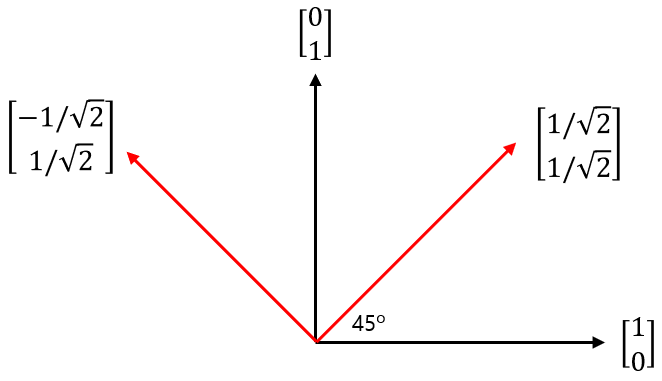
$Drawing$

만약 위 그림과 같이 45도 회전 변환이 발생하였다고 가정하겠습니다.
위와 같은 회전 변환은 기존 벡터에 $\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \\ \end{bmatrix}$ 를 곱해서 변형할 수 있음을 알 수 있습니다.

$Drawing$

그리고 frame1과 frame2는 앞에서 다루었던 예제를 사용하겠습니다.
그러면 frame2에 $[x, y]$ 라는 벡터가 있으면 이 벡터는 $\begin{bmatrix} 3 & 1 \\ 1 & 1 \\ \end{bmatrix}$ transformation matrix에 의하여 frame1에서의 벡터로 변형될 수 있습니다.
- 즉, $\begin{bmatrix} 3 & 1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix}$ 연산을 통하여 frame1에 표현됩니다.
그러면 위 그림과 같이 45도 회전 변환을 해보겠습니다.
- 　$\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 3 & 1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix}$이 됩니다.
- 이 값을 다시 정리하면 frame2에 있던 벡터를 frame1로 mapping 하고 그 벡터를 45도 회전 변환한 것입니다.
마지막으로 frame1에서 회전 변환한 값이 frame2에서는 어떤 값에 해당하는지 알기 위해서는 transformation matrix를 곱해서 frame1 → frame2로 mapping해 줍니다.
즉, $\begin{bmatrix} 3 & 1 \\ 1 & 1 \\ \end{bmatrix}^{-1} = \begin{bmatrix} 1 & -1 \\ -1 & 3 \end{bmatrix}$가 frame1 → frame2로 변환하는 matrix 이므로 곱해줍니다.
- 　$\begin{bmatrix} 1 & -1 \\ -1 & 3 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 3 & 1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix}$이 됩니다.
- 이 값을 다시 정리하면 frame2에 있던 벡터를 frame1로 mapping 하고 그 벡터를 45도 회전 변환한 다음 다시 frame2로 mapping한 값입니다.
- 간략하게 식으로 정리하면 $B^{-1} R B$ 가 됩니다. 이 frame을 변환하는 matrix $B^{-1}, B$로 둘러 쌓이는 형태는 종종 보게 될것입니다.