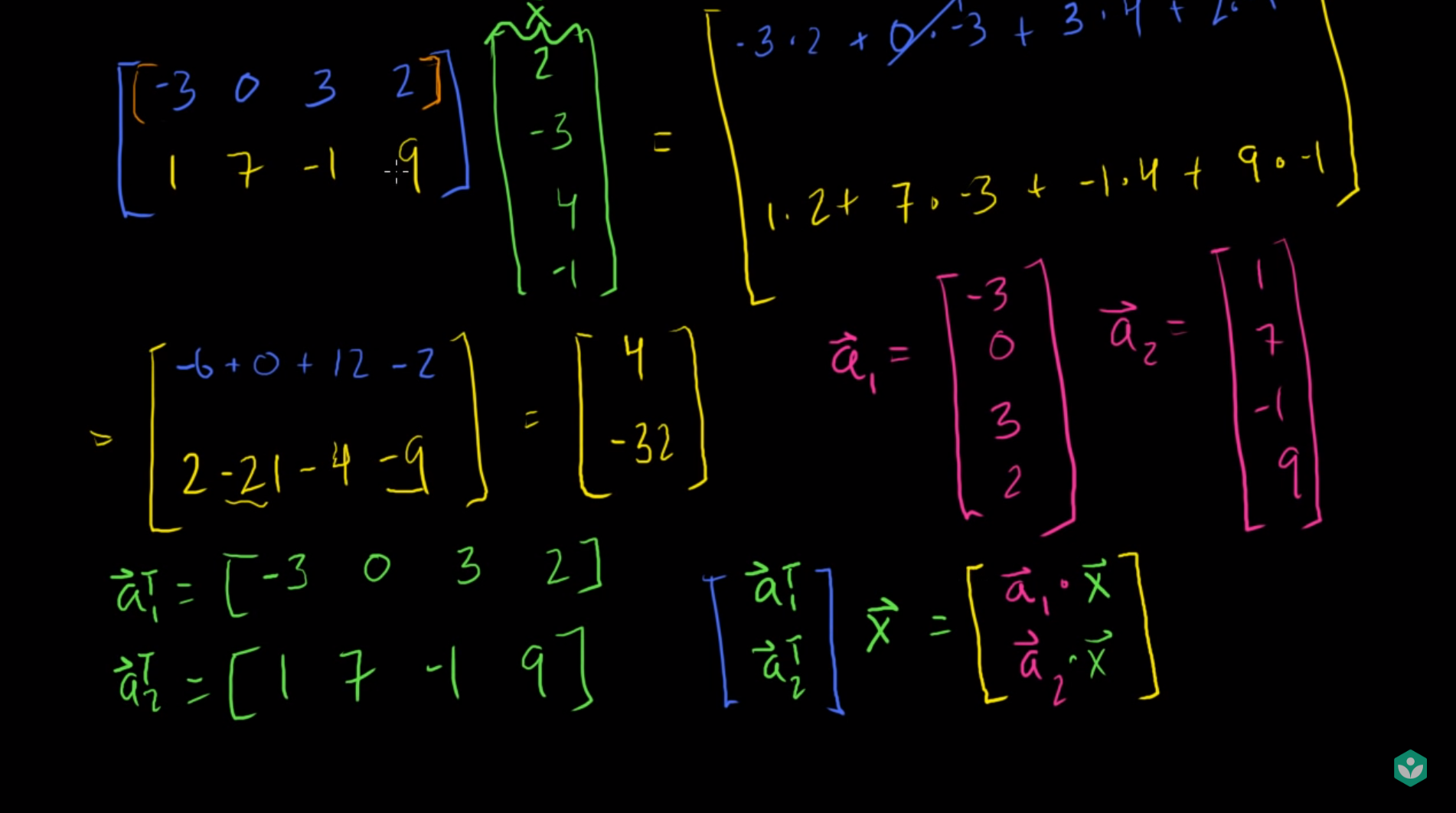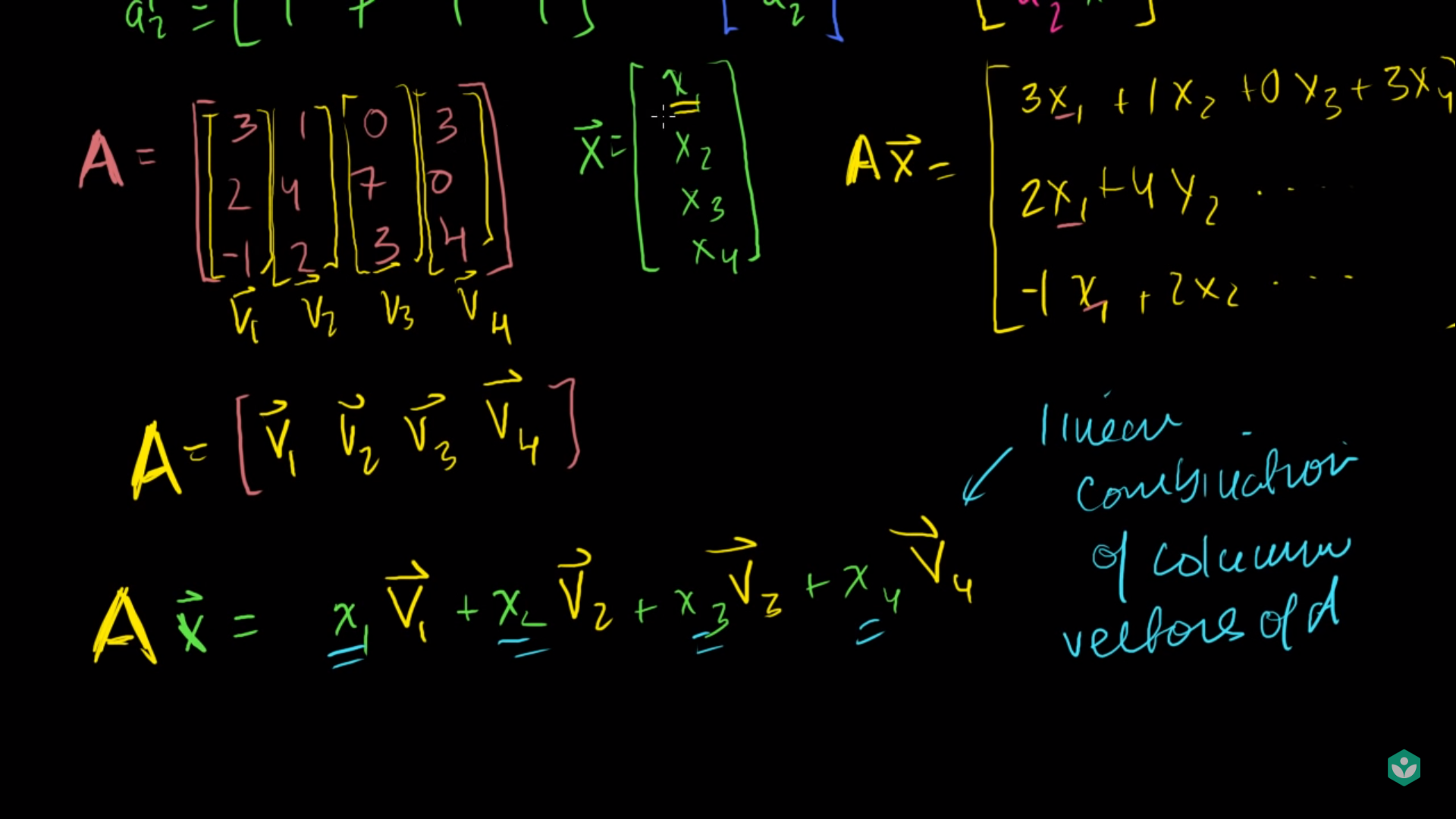행렬 벡터의 곱

출처 : 칸 아카데미 선형대수학, 강의

• 선형대수학 전체 글 목록

• 이번 글에서는 행렬과 벡터를 곱하는 방법에 대하여 알아보도록 하겠습니다.

• 
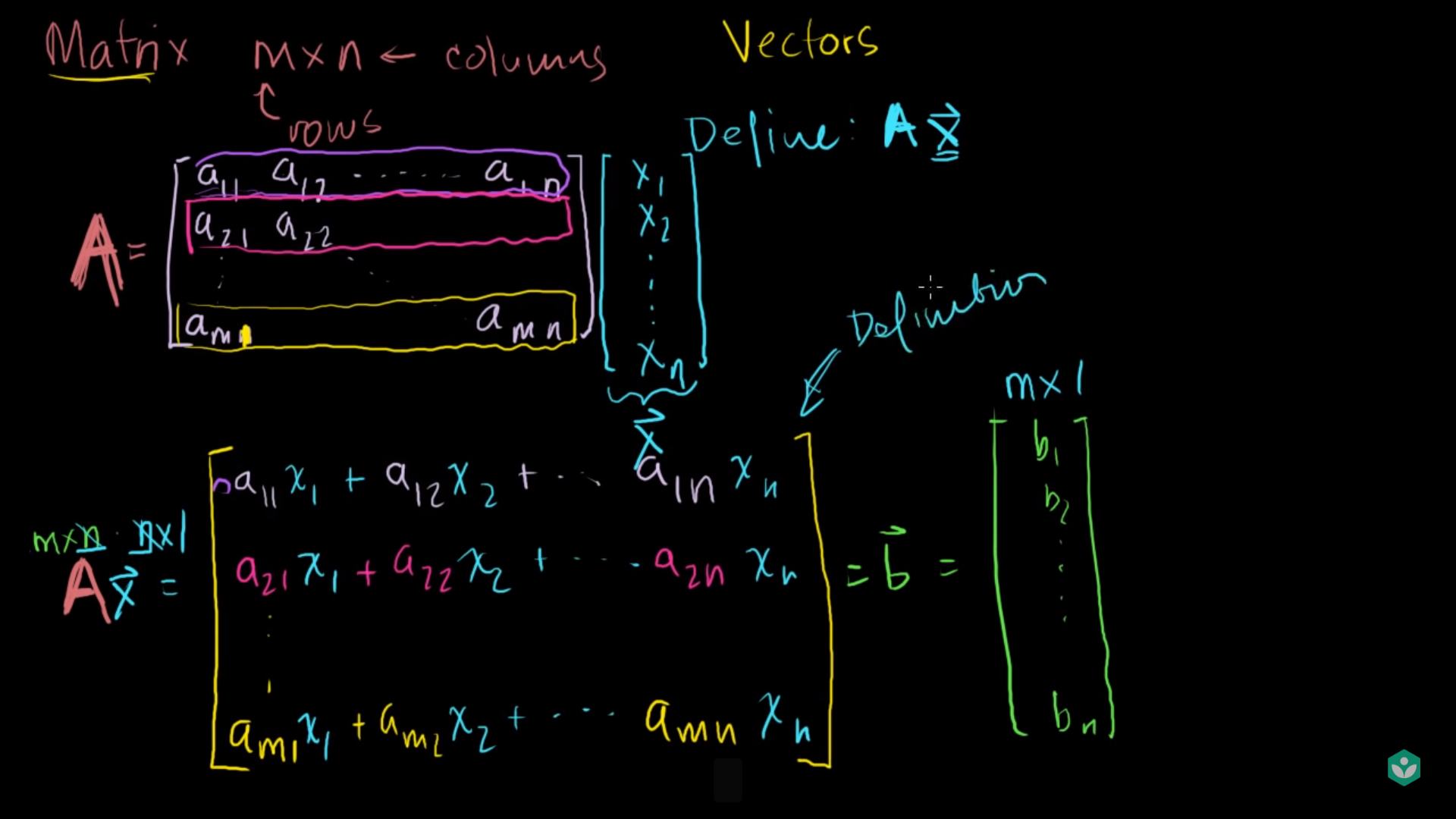
• 먼저 행렬의 크기를 표현할 때, \(m \times n\)으로 표현하고 먼저 사용된 \(m\)을 행의 사이즈로 뒤에 사용된 \(n\)을 열의 사이즈로 간주합니다.
• 행렬에 어떤 벡터를 곱하려면 사이즈가 맞아야 합니다. 즉 행렬의 크기가 \((m, n)\) 이라고 하면 곱해질 벡터는 \((n, 1)\)이 되어야 합니다.
• 위 슬라이드 처럼 각 행과 열의 원소가 차례대로 곱해져서 행렬의 곱이 연산됨을 확인할 수 있습니다.

• 
• 위 슬라이드를 보면 행렬과 벡터의 곱의 예를 좀 더 구체적으로 볼 수 있습니다.
• 이 때, 행렬을 벡터의 집합으로 나타낼 수 있습니다. 오른쪽 중앙에 자주색으로 표시한 \(\vec{a_{1}}, \vec{a_{2}}\)가 행렬을 벡터로 표현한 것입니다.
• 일반적으로 벡터는 열벡터형식으로 표현합니다. 위 행렬에서는 열벡터를 transpose를 취해서 행벡터로 나타내고 행벡터들을 결합해서 행렬로 표시한 것으로 생각해 봅시다.
• 이렇게 행렬을 표현하였을 때, 연산되는 행렬과 벡터의 곱은 다음과 같습니다.
  • 　\(\begin{bmatrix} \vec{a_{1}}^{T} \\ \vec{a_{2}}^{T} \\ \end{bmatrix}\vec{X} = \begin{bmatrix} \vec{a_{1}} \cdot \vec{X} \\ \vec{a_{2}} \cdot \vec{X} \\ \end{bmatrix}\)

• 
• 조금 전 설명드린 것 처럼 벡터는 주로 열벡터를 나타냅니다. 따라서 행렬을 열벡터의 결합으로 생각해 보겠습니다.
• 그러면 행렬 \(A = [\vec{v_{1}}, \vec{v_{2}}, \vec{v_{3}}, \vec{v_{4}}]\)로 나타낼 수 있고 \(A\vec{x} = x_{1}\vec{v_{1}} + x_{2}\vec{v_{2}} + x_{3}\vec{v_{3}} + x_{4}\vec{v_{4}}\) 가 됩니다.
  • 즉 행렬과 열벡터의 곱은 linear combination으로 나타낼 수 있습니다.