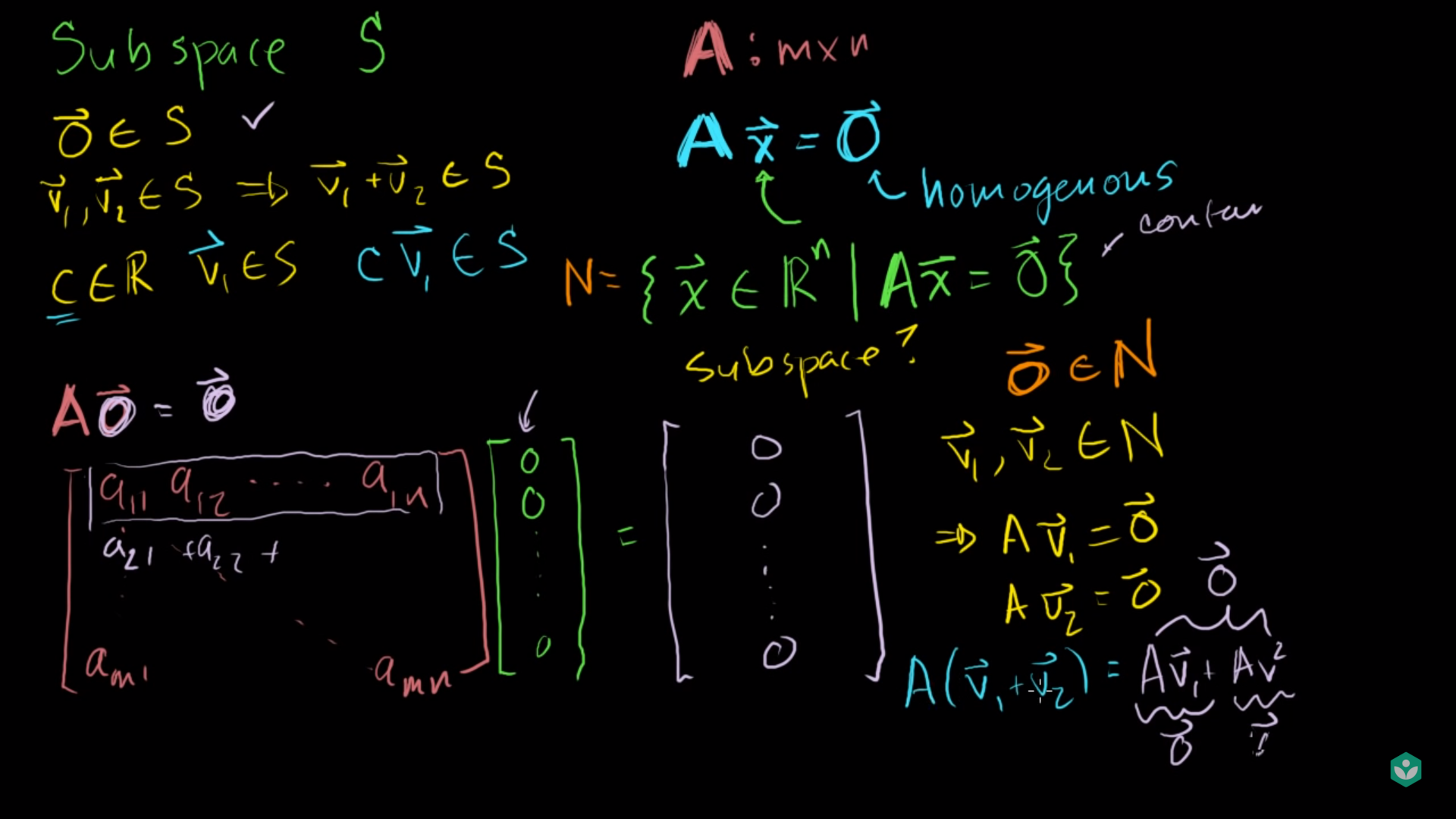행렬의 영공간

출처 : 칸 아카데미 선형대수학, 강의

• 선형대수학 전체 글 목록

• 이번 글에서는 행렬의 영공간에 대하여 알아보도록 하겠습니다.

• 어떤 공간이 부분공간을 만족하려면 다음 세가지 조건을 만족해야 합니다. 부분공간은 $S$ 로 표현하겠습니다.
  • 　$\vec{0} \in S$ … 1조건
    • 영벡터를 포함해야 합니다.
  • 　$\vec{v_{1}}, \vec{v_{2}} \in S \Rightarrow \vec{v_{1}} + \vec{v_{2}} \in S$ … 2조건
    • 덧셈 연산에 대하여 닫혀 있어야 합니다.
  • 　$c \in \mathbb R , \vec{v_{1}} \in S \Rightarrow c\vec{v_{1}} \in S$ … 3조건
    • 스칼라곱 연산에 대하여 닫혀 있어야 합니다.
• 만약 $m x n$ 크기의 행렬 $A$가 있고, 어떤 $\vec{x}$에 의하여 $A\vec{x} = \vec{0}$을 만족한다고 가정해 보겠습니다.
• 이런 조건을 만족하는 $\vec{x}$ 가 존재하고 그런 집합을 $N$ 이라고 한다면 다음과 같이 표현할 수 있습니다.
  • 　$N = \{ \vec{x} \in \mathbb R^{n} \vert A\vec{x} = \vec{0} \}$
  • 만약 이런 조건을 만족하는 벡터들의 집합이 있고 이 집합이 부분공간을 만족하려면 위에서 정의한 1,2,3조건을 모두 만족해야 합니다.
• 결과적으로 집합 N은 부분공간을 만족하고 이 부분공간을 Null space라고 합니다.
• 그러면 Null space가 어떻게 부분공간의 조건을 만족하는지 알아보도록 하겠습니다.