점과 평면 사이의 거리

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

• 선형대수학 전체 글 목록
• 앞의 강의 평면 방정식의 법선 벡터 참조

• 왼쪽 상단의 빨간색 원을 보면 평면 위의 점과 평면 밖의 점을 이용하여 직각 삼각형을 그린 것을 볼 수 있습니다.
• 빨간색 원 안을 보면 초록색 점 $(x_{p}, y_{p}, z_{p})$이 있고 노란색 점 $(x_{0}, y_{0}, z_{0})$이 있습니다.
• 노란색 점 - 초롬색 점을 하면 그림에서 빨간색 벡터 $\vec{f}$ 를 얻을 수 있습니다.
  • ·$\vec{f} = (x_{0} - x_{p})\hat{i} + (y_{0} - y_{p})\hat{j} + (z_{0} - z_{p})\hat{k}$
• 노란색 점에서 평면에 수직인 방향으로 연결하면 벡터 d를 얻을 수 있습니다.
  • 평면과 노란색 점은 수직인 관계라고 가정합니다.
• 이 때, $cos\theta = \frac{d}{\vert \vec{f} \vert}$ 관계를 가집니다.
• 식을 정리하면 $d = \vert \vec{f} \vert cos\theta$ 가 됩니다.
• 식을 변형하여 분모 분자에 $\vert \vec{n} \vert$ 를 곱하겠습니다.
  • ·$d = \frac{ \vert \vec{n} \vert \ \vert \vec{f} \vert cos\theta }{ \vert \vec{n} \vert }$
• 위 식에서 분자를 보면 $\vert \vec{n} \vert \ \vert \vec{f} \vert cos\theta = \vec{n} \cdot \vec{f}$ 가 됩니다.

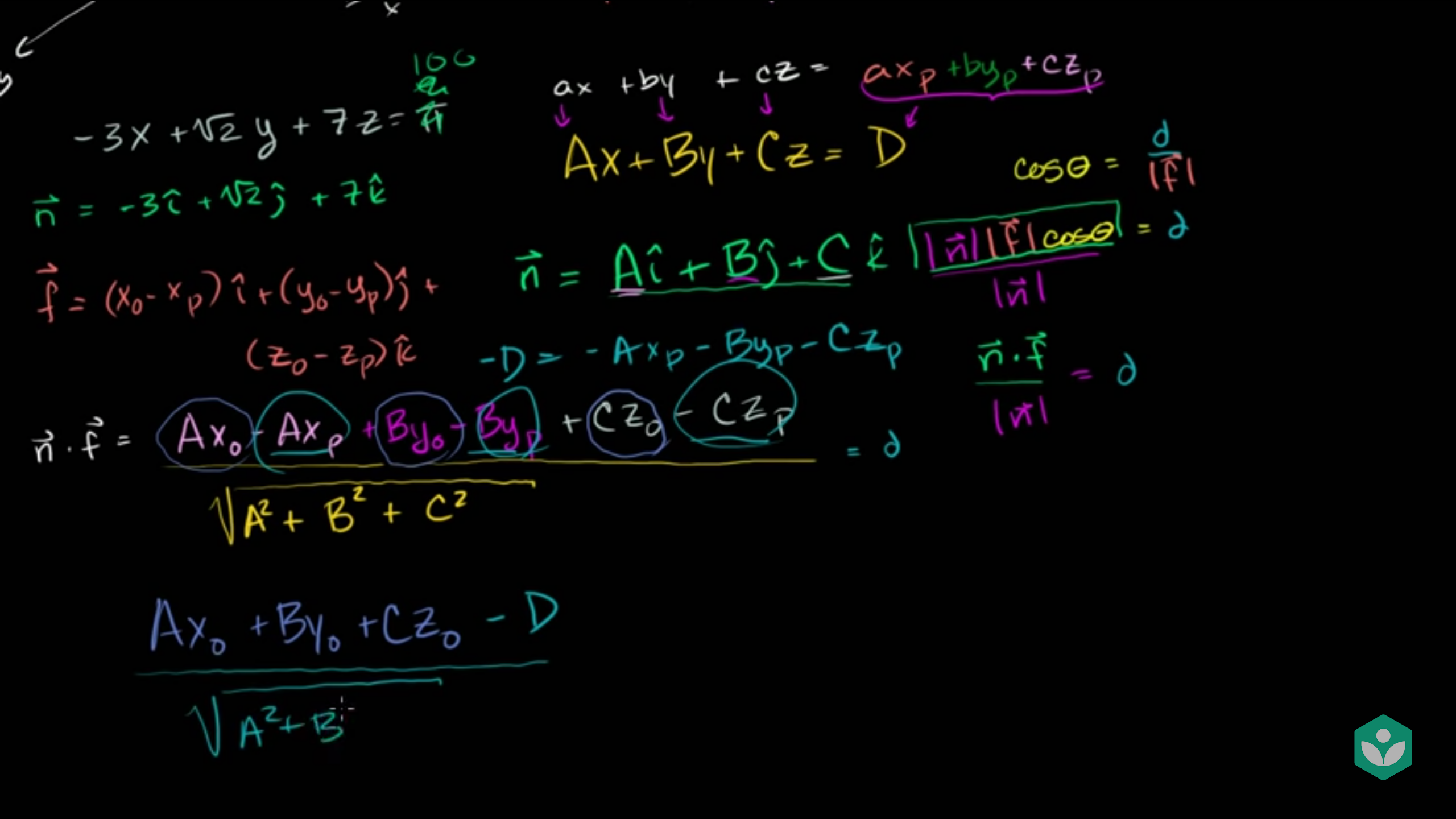
• ·$d = \frac{\vec{n} \cdot \vec{f}}{ \vert \vec{n} \vert }$를 전개해 보겠습니다.
• ·$d = \frac{\vec{n} \cdot \vec{f}}{ \vert \vec{n} \vert } = \frac{ Ax_{0} - Ax_{p} + By_{0} - By_{p} + Cz_{0} - Cz_{p} }{ \sqrt{A^{2} + B^{2} + C^{2}} }$
  • 이 때 $Ax_{p} + By_{p} + Cz_{p}$는 평면의 방정식 $Ax + By + Cz = D$에서의 D에 해당합니다. (앞 강의 참조)
• 따라서 점과 평면사이의 거리는 $\frac{ Ax_{0} + By_{0} + Cz_{0} - D }{ \sqrt{A^{2} + B^{2} + C^{2}} }$ 가 됩니다.

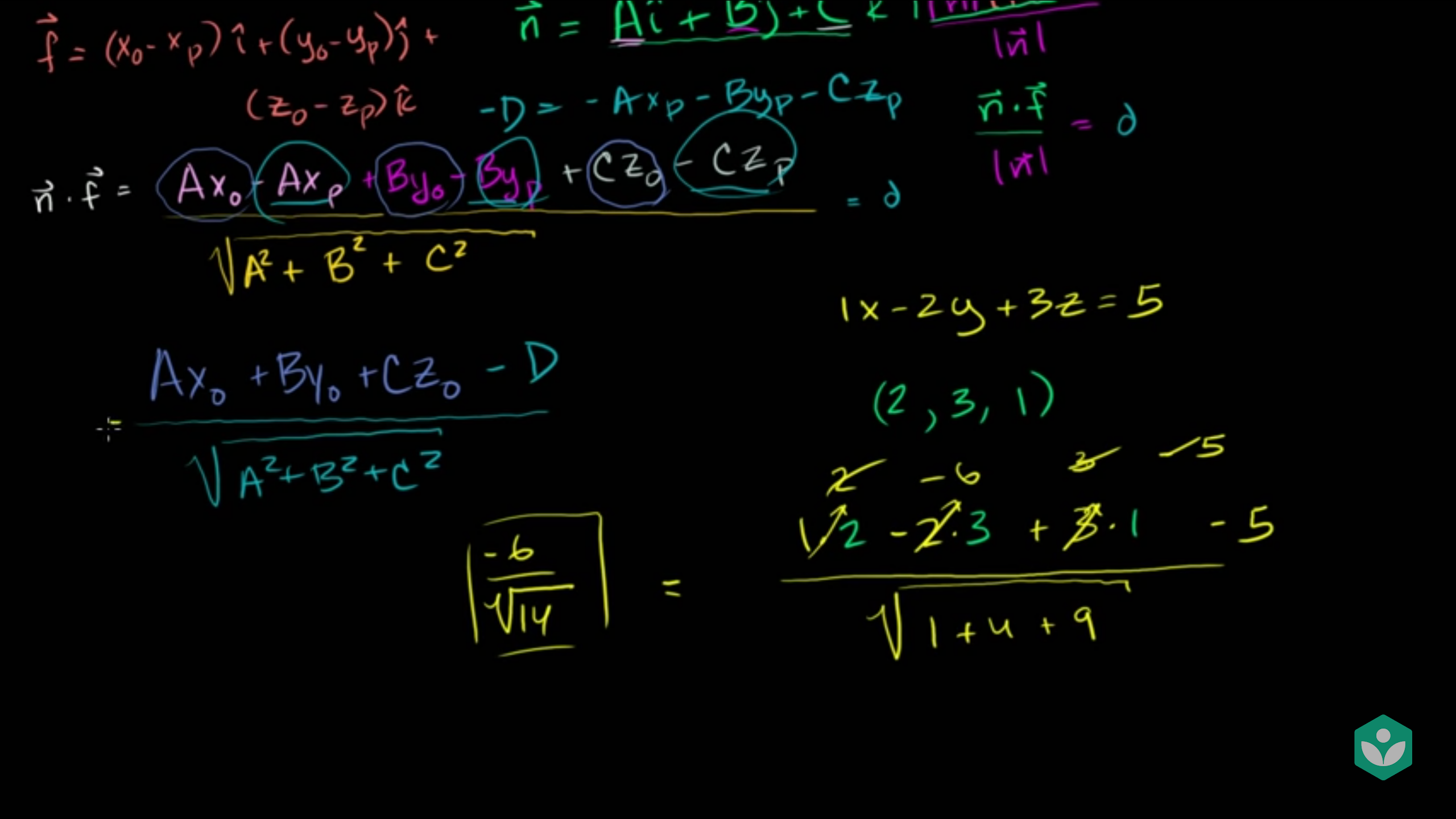
• 예를 들어, 점 (2, 3, 1)과 평면 $x - 2y + 3z = 5$ 의 거리를 구하면 (등식이 성립하지 않으므로 공간 상에 존재 하지 않습니다.)
  • ·$\frac{1 \cdot 2 - 2 \cdot 3 + 3 \cdot 1 - 5}{ \sqrt{ 1 + 4 + 9} } = \frac{-6}{\sqrt{14}}$