
행 사다리꼴 행렬을 이용하여 3차연립방정식과 4개의 변수 풀기
2017, Mar 01
출처 : 칸 아카데미 선형대수학, 비디오
-
이번 글에서 살펴볼 문제는 식의 갯수 보다 변수의 갯수가 많아서 자유 변수가 존재하는 즉, 해가 무한히 많은 형태의 선형 연립 방정식을 풀어보겠습니다.
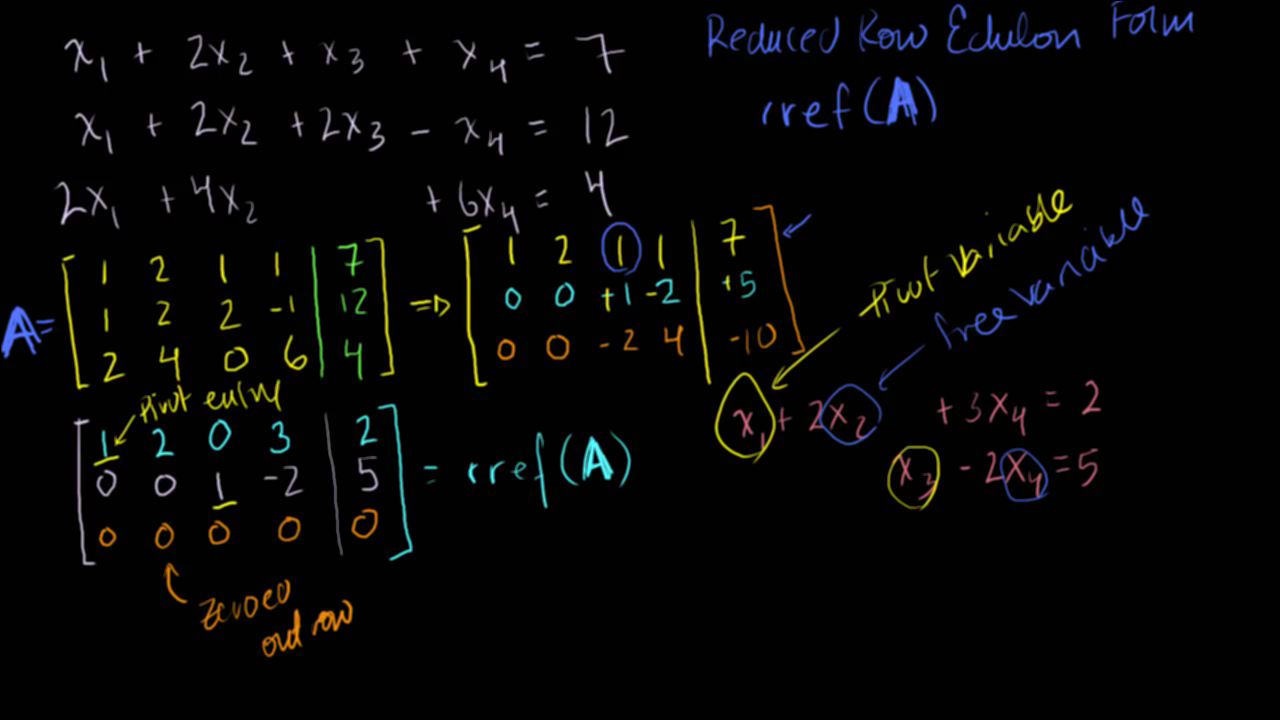
- 위 슬라이드를 보면 미지수는 4개이고 식은 3개입니다. 이 때에는 무한히 많은 해를 얻는 다는 것을 익히 알고 있습니다.
- 위 방정식 3개를 노란색 행렬처럼 계수만 가져오도록 하겠습니다.
- 이 때, 우변의 항도 행렬에 같이 쓸 수 있는데, 좌변의 계수(coefficient)와 우변의 상수값을 같이 하나의 행렬에 적는 것을 augmented matrix(확대 행렬) 이라고 합니다.
- 이런 행렬을 정리를 하여 원하는 solution을 찾아야 하는데, 이 방법을
Reduced Row Echelon Form이라고 합니다.- 줄여서 rref 라고 합니다.
- echelon이 사다리꼴의 뜻을 가집니다.
- 먼저 Reduced ref와 그냥 ref의 차이는 rref에서는 한 열에서 pivot은 1이고 pivot을 제외한 다른 값들은 0이된 형태입니다.
- pivot은 한 행에서 0이 아닌 가장 앞선 값을 말합니다.
- 각 행 당 pivot이 한개 있을 수 있고 상황에 따라서는 pivot이 없는 경우도 있을 수 있습니다.
- 확대행렬에서는 행 간의 덧셈과 뺄셈을 하여도 결과는 변하지 않습니다.
- 단순히 생각하면 연립방정식을 풀 때에도 A와 B라는 식이 있을 때 2A + B 등과 같이 양변에 어떤 값을 곱한 뒤 더하여 변수를 소거하곤 하였습니다.
- 영상을 보시면 자세한 계산 과정을 보실 수 있습니다. 계산 과정의 목적은 사다리꼴 형태로 위의 식에서 pivot이 먼저 나오도록 변형하는 것입니다.
- 위 예제에서는 rref로 표현을 해보니 마지막 행이 0으로만 구성된 행이 되었습니다.
- 정리한 식의 결과는 다음과 같습니다.
- ·\(x_{1} + 2x_{2} + 3x_{4} = 2\)
- ·\(x_{3} -2x_{4} = 5\)
- 이 때, \(x_{1}, x_{3}\)는 pivot에 해당하므로 값을 정의할 수 있는 형태입니다. 이것을
pivot variable이라고 합니다. - 반면 \(x_{2}, x_{4}\)는 pivot에 해당하는 값이 없으므로 값을 정의할 수 없는 형태입니다. 이것을
free variable이라고 하고 어떤 값이라도 올 수 있도록 변수로 정의합니다.
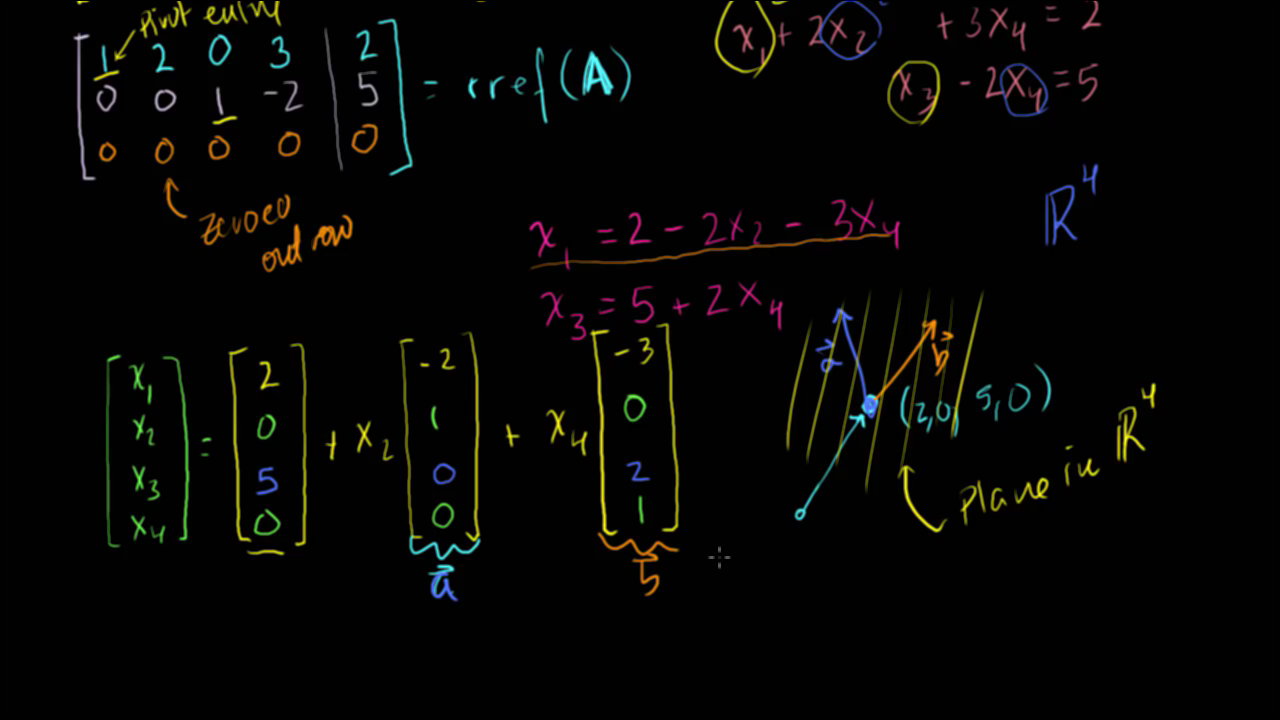
- 따라서 \(x_{1}, x_{3}\)을 정리하면 자주색 식과 같이 free variable인 \(x_{2}, x_{4}\)를 이용하여 식을 세울 수 있습니다.
- ·\(x_{1} = 2 - 2x_{2} -3x_{4}\)
- ·\(x_{3} = 5 + 2x_{4}\)
- 위 식을 행렬을 이용하여 정의 하면 다음과 같습니다.
- \[\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \\ 5 \\ 0 \\ \end{bmatrix} + x_{2}\begin{bmatrix} -2 \\ 1 \\ 0 \\ 0 \\ \end{bmatrix} +x_{4}\begin{bmatrix} -3 \\ 0 \\ 2 \\ 1 \\ \end{bmatrix}\]
- 이 때, x2와 x4에 곱해지는 벡터를 \(\vec{a}, \vec{b}\)로 두겠습니다.
- 이를 기하적으로 접근하면 \(\mathbb R^{4}\) 공간속에서 오른쪽 하단 같은 평면을 그릴 수 있습니다.
- 솔루션의 상수항을 기점으로 각 벡터의 합으로 표시가 됩니다.
- ·\(\mathbb R^{4}\)에서 2차원 평면으로 해가 나오는 이유는 free variable의 갯수가 2개 이기 때문입니다.
- 만약 free variable의 갯수가 1개였다면 선으로 해가 나올 것이고 free variable의 갯수가 없다면 유일한 해로 점의 형태로 나타날 수 있습니다.