행 사다리꼴을 이용하여 선형계 증 해는 경우 확인하기

출처 : 칸 아카데미 선형대수학, 강의

• 선형대수학 전체 글 목록

• 이번 글에서는 RREF 를 이용하여 선형연립방정식에서 해가 없는 경우에 대하여 알아보도록 하겠습니다.

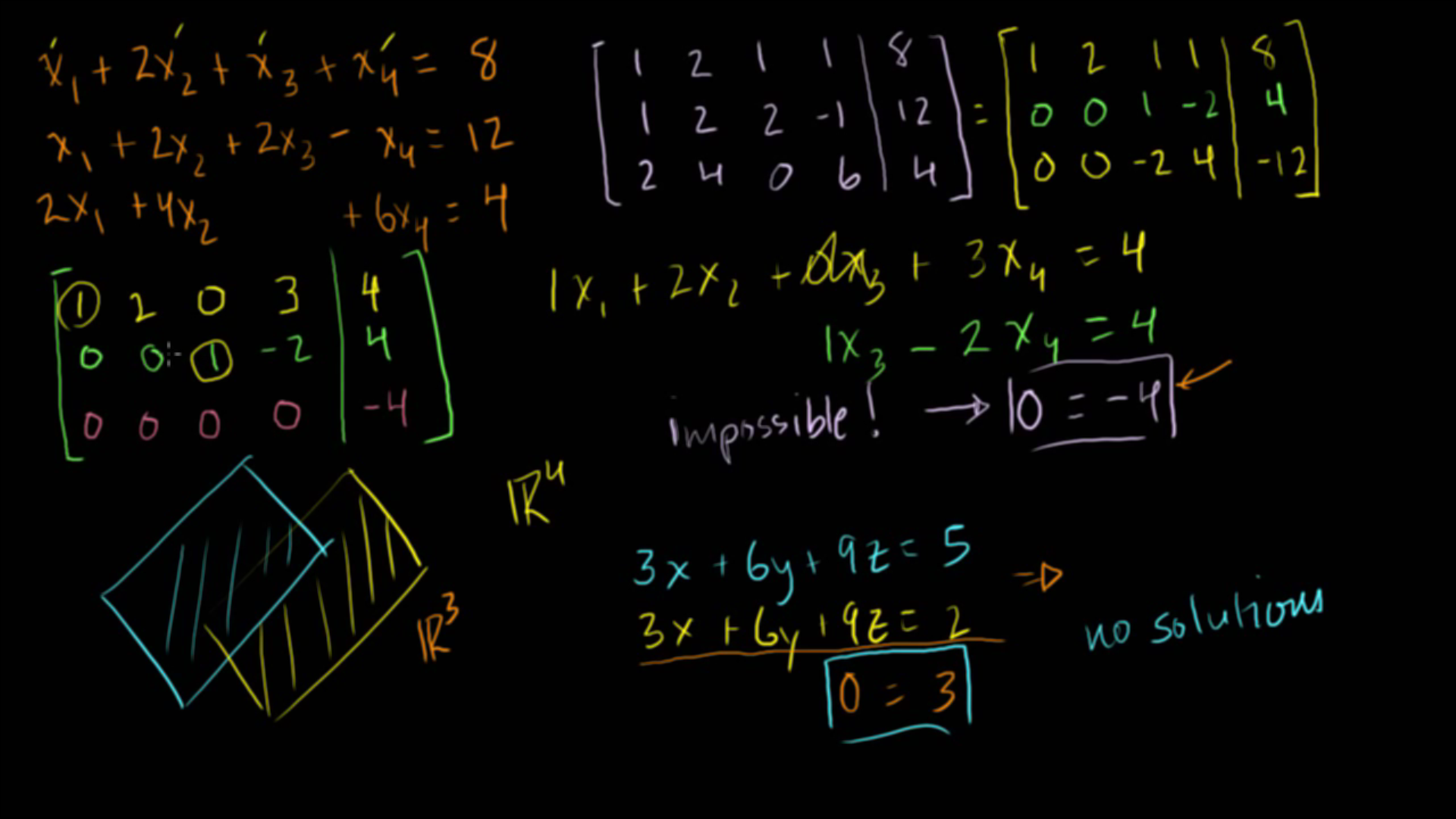
• 왼쪽 상단의 3개의 선형식을 이용하여 확대 행렬을 만들어 보겠습니다. (보라색 행렬과 같이 만들 수 있습니다.)
• 다음으로 1행을 2행과 3행에 연산을 시키면 오른쪽 상단의 노란색 행렬과 같이 구할 수 있습니다.
• 다음으로 2행을 1행과 3행에 연산을 시키면 왼쪽 가운데의 초록색 행렬과 같이 구할 수 있습니다.
• 이 때 3행을 보면 [0 0 0 0 -4 ] 의 형태를 가지게 됩니다.
  • 즉, 최초의 pivot이 마지막 열에 있게 되는데 식으로 치면 0 = -4 가 되어 불가능한 형태가 되어버립니다.
• 즉, \(\mathbb R^{4}\) 에서 위 선형식 3개는 교차하지 않는다고 봐야하며 따라서 해가 없다고 판단할 수 있습니다.
• 예를 들면 위 슬라이드 하단의 \(\mathbb R^{3}\) 공간의 식 2개를 살펴보겠습니다.
  • ·\(3x + 6y + 9z = 5\)
  • ·\(3x + 6y + 9z = 2\)
  • 즉 \(0 = 3\) 이 되어 해가 없게됩니다.
  • 이것은 왼쪽 하단과 같이 교차점이 없어서 해가 없게되는 형태라고 볼 수 있습니다.

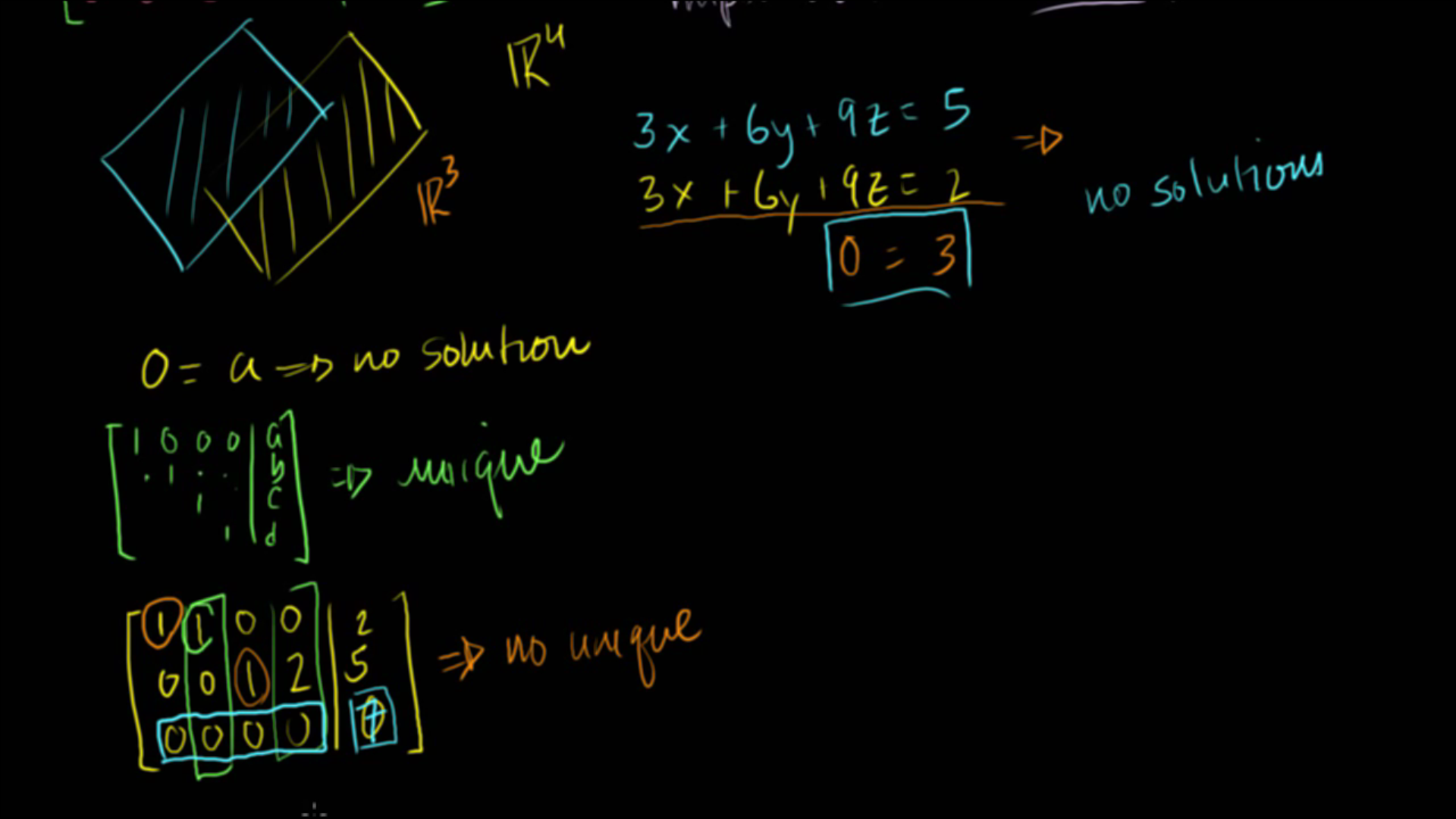
• rref의 결과에 따라서 어떤 해를 가지게 되는 지 나뉘게 됩니다.
• 1 ) rref 에서 [0 0 … 0 a ] 의 형태를 가지고 \(a \neq 0\)인 행이 있다면 해는 없습니다.
• 2 ) rref 에서 [0 0 … 0 0 ]의 형태를 가지는 행이 있다면 해는 무한히 많습니다.
  • 즉 자유 변수를 가지게 되는 조건 입니다.
• 3 ) rref 에서 모든 열이 pivot = 1인 행을 가지고 있다면 해는 유일 합니다.