Reflecting in a plane
2018, Sep 27
- 이번 글에서는 앞에서 배웠던 그램 슈미트, 정규직교 등을 이용하여 transformation 좀 더 쉽게 하는 방법에 대하여 알아보겠습니다.
- 즉, transformation 지식과 basis에 관한 지식을 이용할 예정입니다.
- 정확하게 말하면 앞에서 배웠던 정규직교를 왜 배웠을까에 대한 의문을 해소하는 예제가 될 수 있을것 같습니다.
- 이번 글의 목적은 어떤 벡터가 있을 때, 그 벡터의 reflection을 구해보려고 합니다. 즉, 벡터를 평면을 기준으로 대칭시키면 reflection을 찾을 수 있습니다.
- 임의의 공간에 있는 벡터를 평면을 기준으로 reflection하려면 평면과 평면과 직교한 또 하나의 벡터가 필요합니다. 그램 슈미트 과정을 이용하면 쉽게 구할 수 있습니다.

- 이번 글에서 다룰 예제는 3개의 벡터(\(v_{1}, v_{2}, v_{3}\))로 이루어진 공간입니다.
- 벡터는 각각 \(v_{1} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}, v_{2} = \begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix}, v_{3} = \begin{bmatrix} 3 \\ 1 \\ -1 \\ \end{bmatrix}\)이 됩니다.
- 먼저 주어진 3개의 벡터를 이용하여 그램 슈미트 과정을 거치면 정규직교기저 3개를 구할 수 있습니다. 구해보겠습니다.
- 첫째로 \(e_{1} = \frac{v_{1}}{\vert v_{1} \vert} = \frac{1}{\sqrt{3}} \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}\) 가 됩니다.
- 두번째로 \(u_{2} = v_{2} - (v_{2} \cdot e_{1})e_{1} = \Biggl( \begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} - \begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} \cdot \frac{1}{\sqrt{3}} \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} \Biggr) \frac{1}{\sqrt{3}} \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \\ 0 \\ \end{bmatrix}\)
- 정리하면, \(e_{2} = \frac{u_{2}}{\vert u_{2} \vert} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1 \\ 0 \\ \end{bmatrix}\) 이 됩니다.
- 마지막으로 \(u_{3} = v_{3} - (v_{3} \cdot e_{1})e_{1} - (v_{3} \cdot e_{2})e_{2} = \begin{bmatrix} 3 \\ 1 \\ -1 \\ \end{bmatrix} - \Biggl( \begin{bmatrix} 3 \\ 1 \\ -1 \\ \end{bmatrix} \cdot \frac{1}{\sqrt{3}} \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} \Biggr) \frac{1}{\sqrt{3}} \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} - \Biggl( \begin{bmatrix} 3 \\ 1 \\ -1 \\ \end{bmatrix} \cdot \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1 \\ 0 \\ \end{bmatrix} \Biggr) \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ -2 \\ \end{bmatrix}\)가 됩니다.
- 정리하면, \(e_{3} = \frac{u_{3}}{\vert u_{3} \vert} = \frac{1}{\sqrt{6}} \begin{bmatrix} 1 \\ 1 \\ -2 \\ \end{bmatrix}\) 가 됩니다.
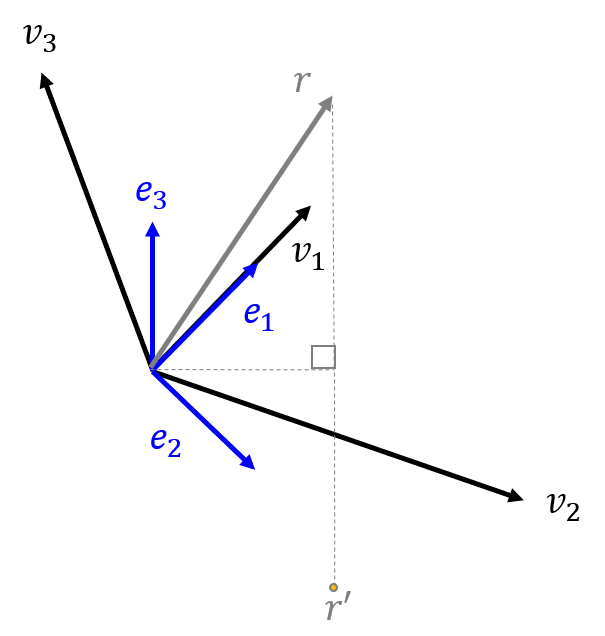
- 앞에서 계산한 내용을 정리해 보겠습니다.
- 먼저 위 그림을 보면 기존의 벡터 \(v_{1}, v_{2}, v_{3}\)가 있고, 그램 슈미트 과정을 통하여 \(e_{1}, e_{2}, e_{3}\)를 구하였습니다. \(e_{3}\)는 \(e_{1}, e_{2}\)를 이용하여 만든 평면과 직교합니다.
- 그러면 \(v_{1}, v_{2}, v_{3}\)을 기준으로 만들어진 공간을 frame_v이라고 하고 \(e_{1}, e_{2}, e_{3}\)를 이용하여 만들어진 공간을 frame_e라고 하겠습니다.
- 현재 위 그림의 벡터 \(r\)을 \(e_{3}\) 축으로 대칭 되는 \(r'\)으로 transformation 해보려고 합니다. 즉 \(r\)을 \(r'\)로 변형해야 하지요.
- 그런데 frame_v에서 바로 \(r \to r'\) 로 transformation하는 것은 생각 보다 쉽지 않습니다. 왜냐하면 frame_v의 벡터가 계산하기 쉽지가 않기 때문입니다.
- 벡터 사이의 각도도 애매하고 정확히 어떻게 해야 \(e_{3}\) 축으로 대칭되는 벡터를 찾을지 감이 잡히지 않습니다. 따라서 다음과 같이 좀 더 과정을 거쳐서 접근해 보겠습니다.
- 먼저 \(E = (e_{1}, e_{2}, e_{3})\)는 frame_e → frame_v로 mapping 하는 행렬입니다.
- 그리고 frame_e에서 \(e_{3}\) 방향으로 대칭하는 transformation matrix \(T_{E} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{bmatrix}\)가 됩니다.
- 앞에서 설명한 바와 같이 \(e_{1}\) 과 \(e_{2}\)는 서로 직교하고 이 두 벡터로 만든 평면과 \(e_{3}\)는 직교합니다.
- 먼저 frame_v에 있는 벡터 \(r\)을 frame_e 로 mapping 해주어야 합니다. \(E\)의 정의에 따라 \(E^{-1}\)이 그 역할을 할 수 있습니다.
- 따라서 \(r_{E} = E^{-1}r\) 이 됩니다.
- 참고로 \(E\)는 직교 행렬이기 때문에 \(E^{-1} = E^{T}\)가 되므로 쉽게 계산할 수 있습니다.
- 다음으로 transformation matrix를 통하여 frame_e상에서 transformation을 해줍니다. 따라서 \(r'_{E} = T_{E}E^{-1}r\)이 됩니다.
- 이제 frame_e에서는 transformation이 되었으니 다시 frame_v로 mapping 시켜주어야 합니다.
- 즉, \(r' = ET_{E}E^{-1}r = E T_{E} E^{T} r\) 가 됩니다.
- 위 과정을 모두 거치면 \(r \to r'\)로 transformation이 됩니다.
- 계산 과정은 다음과 같습니다.
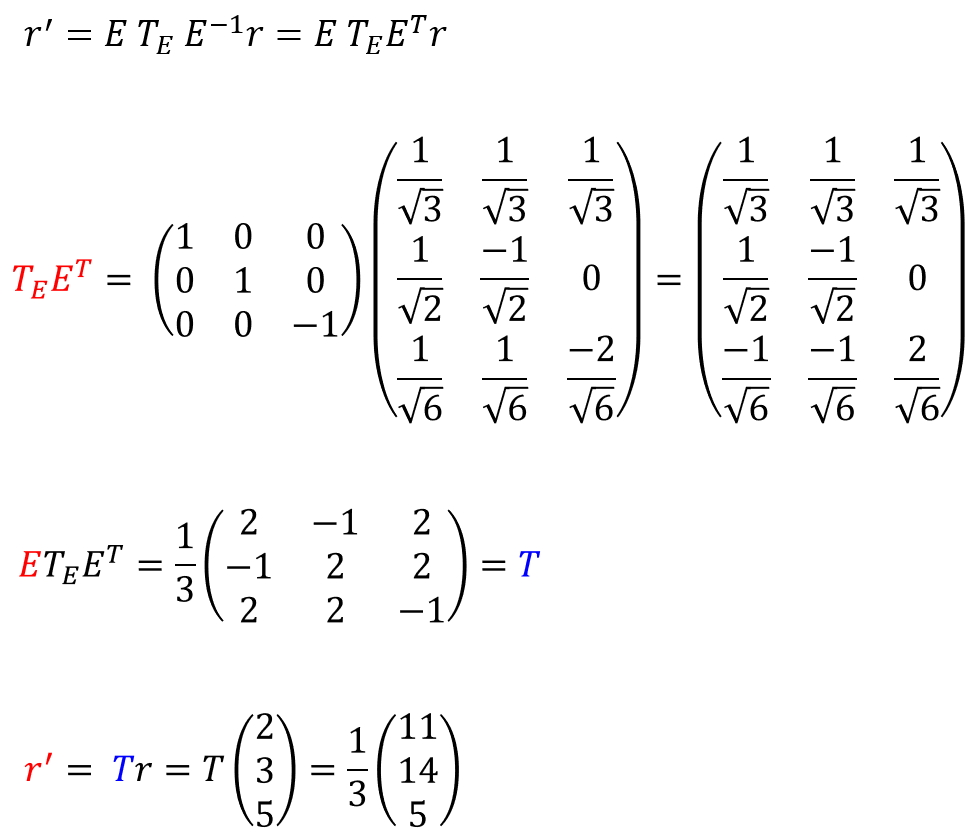
- 정리하면 변환 과정은 다음과 같습니다.
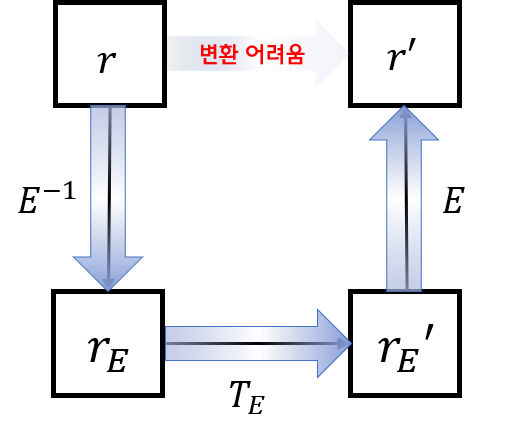
- 이번 글의 핵심은 그람 슈미트 방법을 이용하여
정규직교벡터를 구하여 transformation에 어떻게 적용하는 지 였습니다.
- Relfleting in a plane 예제
- 위 예제를 보시면 아래 결과에 판다 그림이 평면을 기준으로 reflection되어 있음을 볼 수 있습니다.
- 연갈색 선이 기존의 basis이고 보라색 선이 그램 슈미트 과정을 통하여 얻은 정규 직교 벡터로 된 basis입니다.
- 정규 직교 벡터 basis로 transformation 한 다음 reflection을 하고 다시 기존의 basis로 transformation을 하면 위와 같이 reflection한 형상을 얻을 수 있습니다.