Symmetry of dot product
2018, Sep 27
- 이번 글에서는 dot product의 기하학적인 대칭에 대하여 간단하게 보겠습니다.
- 임의의 벡터 \(\hat{v}\)와 유닛 벡터를 dot product 하여 대칭성에 대하여 다루어 보겠습니다.
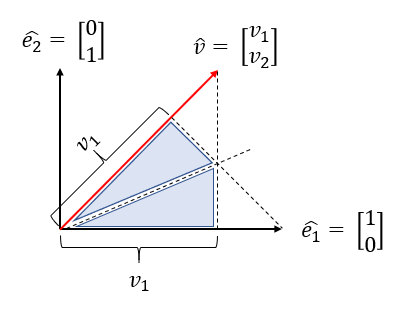
- 위에 그래프를 보면 \(\hat{v}\)에서 \(\hat{e_{1}}\)으로 projection을 한 것을 보면 projection 한 것의 크기가 \(v_{1}\)임을 알 수 있습니다.
- 이 값의 크기는 \(\hat{v} \cdot \hat{e_{1}}\)과 같습니다.
- 산술적인 계산에서는 벡터의 내적에는 교환법칙이 성립하는데 위의 그래프를 보면 기하학적으로도 대칭성이 존재함을 알 수 있습니다.
- 즉, 앞의 방법과 반대로 \(\hat{e_{1}}\)에서 \(\hat{v}\)로 projection을 하면 그 크기 또한 \(v_{1}\)이 됩니다.
- 각각의 projection의 교차점을 중심으로 생기는 삼각형을 보면 동일한 크기의 삼각형임을 알 수 있는데 이 것이 기하학적으로도 projection의 결과가 대칭임을 확인할 수 있는 방법입니다.
- 따라서 projection은 대칭적이고 dot product 또한 대칭적이며 왜 projection이 dot product 인지 알 수 있습니다.