벡터의 내적과 벡터의 길이 (Vector dot product and vector length)

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

이번 글에서는 벡터의 내적과 벡터의 길이에 대하여 알아보도록 하겠습니다.

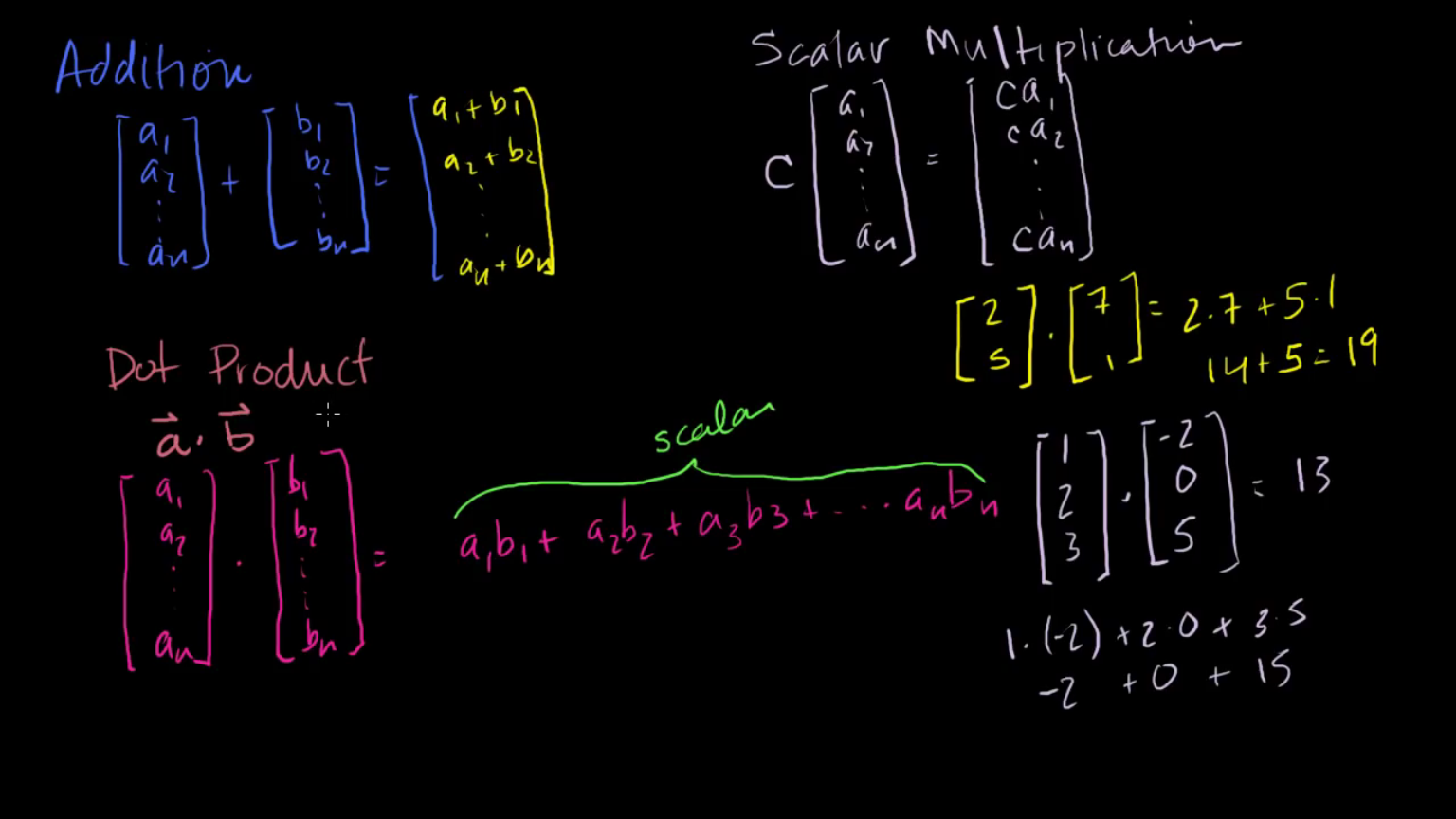
$Drawing$

먼저 앞의 글에서 다루었던 것 처럼 벡터에 대한 덧셈 연산과 스칼라 곱에 대한 내용을 아신 다는 전제 하에서 진행하겠습니다.
- 위의 슬라이드의 Addition과 Scalar Multiplication의 내용을 참조하시기 바랍니다.
위의 Scalar Multiplication은 단지 벡터를 스칼라 배 한것으로 크기만 키운것에 해당합니다.

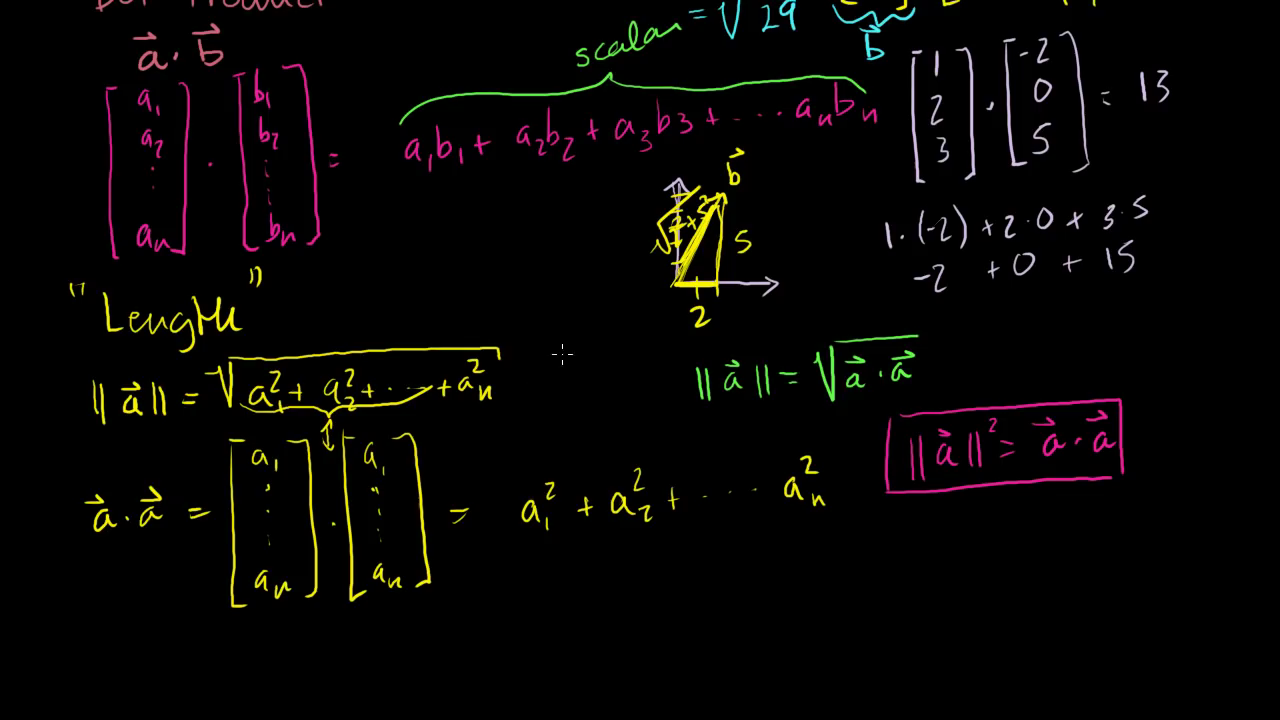
$Drawing$

이번 강의에서 다룰 내용은 Dot Product 입니다.
위의 예제처럼 두 벡터를 Dot Product를 하면 $a_{1}b_{1} + a_{2}b_{2} + ... + a_{n}b_{n}$ 이 됩니다.
- 즉 dot product의 결과는 벡터가 아니라 스칼라 입니다.
- 위 슬라이드의 예제를 보면 두 벡터의 dot product는 스칼라가 됨을 알 수 있습니다.
이번 강의에서 다루는 또 다른 내용은 Length 입니다.
벡터에서의 Length는 2,3차원에서 그려지는 선의 길이라는 개념을 넘어 N 차원에서의 길이라는 개념을 포함하고 있습니다.
벡터에서의 Length의 정의는 $\|\vec{a}\| = \sqrt{a_{1}^{2} + a_{2}^{2} + ... + a_{n}^{2} }$ 입니다.
- 2차원에서는 피타고라스의 정리와 똑같은 식이지만 N 차원 까지 확장시킬 수 있습니다.
Length와 Dot Product를 연관시켜 보겠습니다.
Length는 정확히 어떤 벡터 자기 자신과의 Dot Product에 해당합니다.
- 즉, $\|\vec{a}\| = \sqrt{\vec{a} \cdot \vec{a}}$ 입니다.
- 또는 $\|\vec{a}\|^{2} = \vec{a} \cdot \vec{a}$ 에 해당합니다.
다음 글에서 벡터의 Length와 Dot Product에 대한 성질에 대하여 다루어 보도록 하겠습니다.