벡터의 삼각부등식

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

• 선형대수학 전체 글 목록

이번 글에서는 앞에 글에서 배운 코시 슈바르츠 부등식을 이용하여 벡터의 삼각 부등식에 대하여 배워 보도록 하겠습니다.

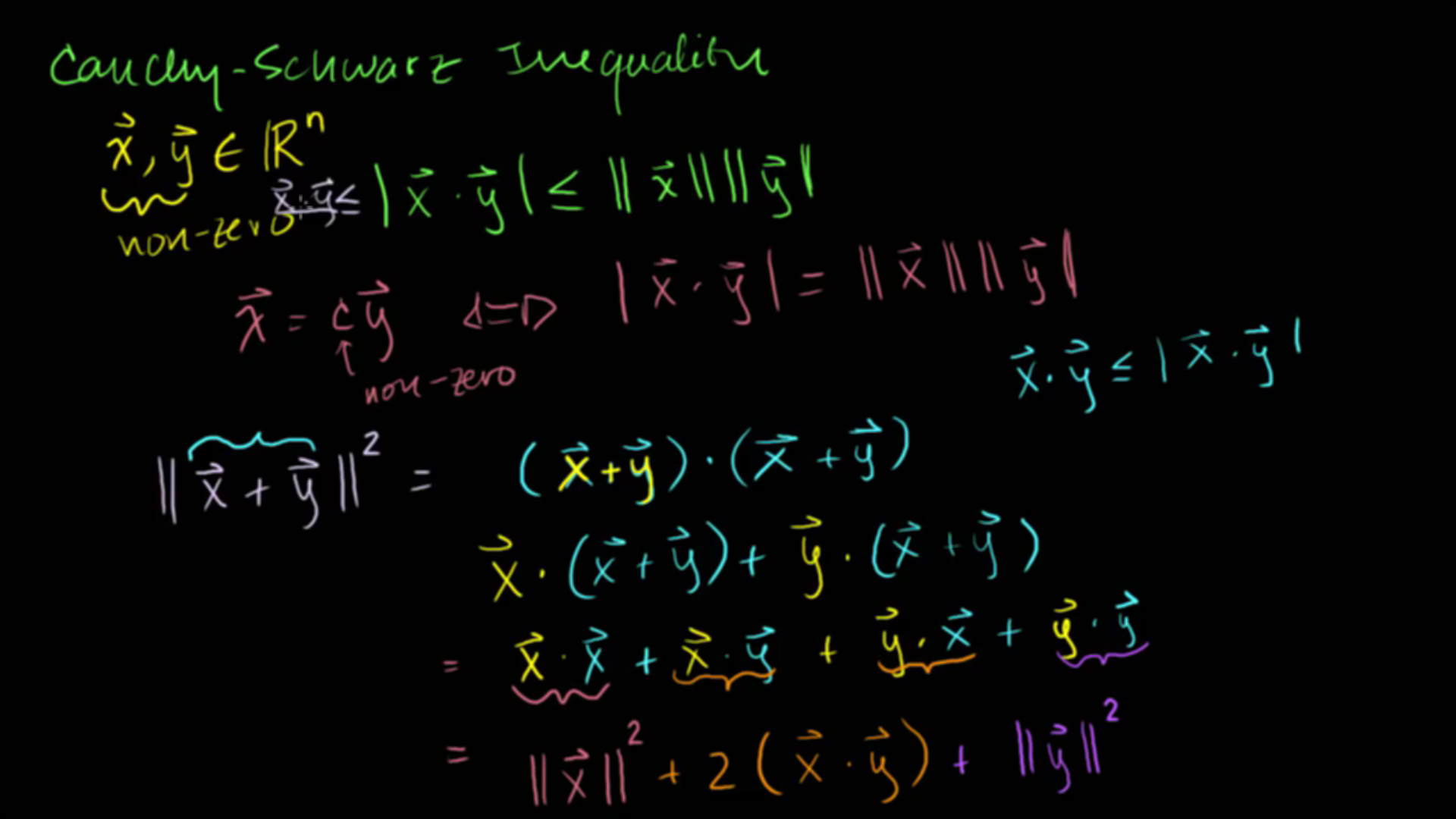
• 위 슬라이드에서 연두색 글자에 해당하는 코시 슈바르츠 부등식을 명확히 이해하셨다면 이번 글은 쉽게 이해가 가실 겁니다.
  • 코시 슈바르츠 부등식에서 등호가 성립하는 조건은 \(\vec{x} = c \vec{y}\) 조건을 가질 때 입니다.
• 코시 슈바르츠 부등식은 다양한 식을 증명할 때 많이 사용되곤 합니다.
• 위 슬라이드 처럼 \(\Vert \vec{x} + \vec{y} \Vert^{2}\) 를 풀어서 적어보면 위와 같이 정리할 수 있습니다.

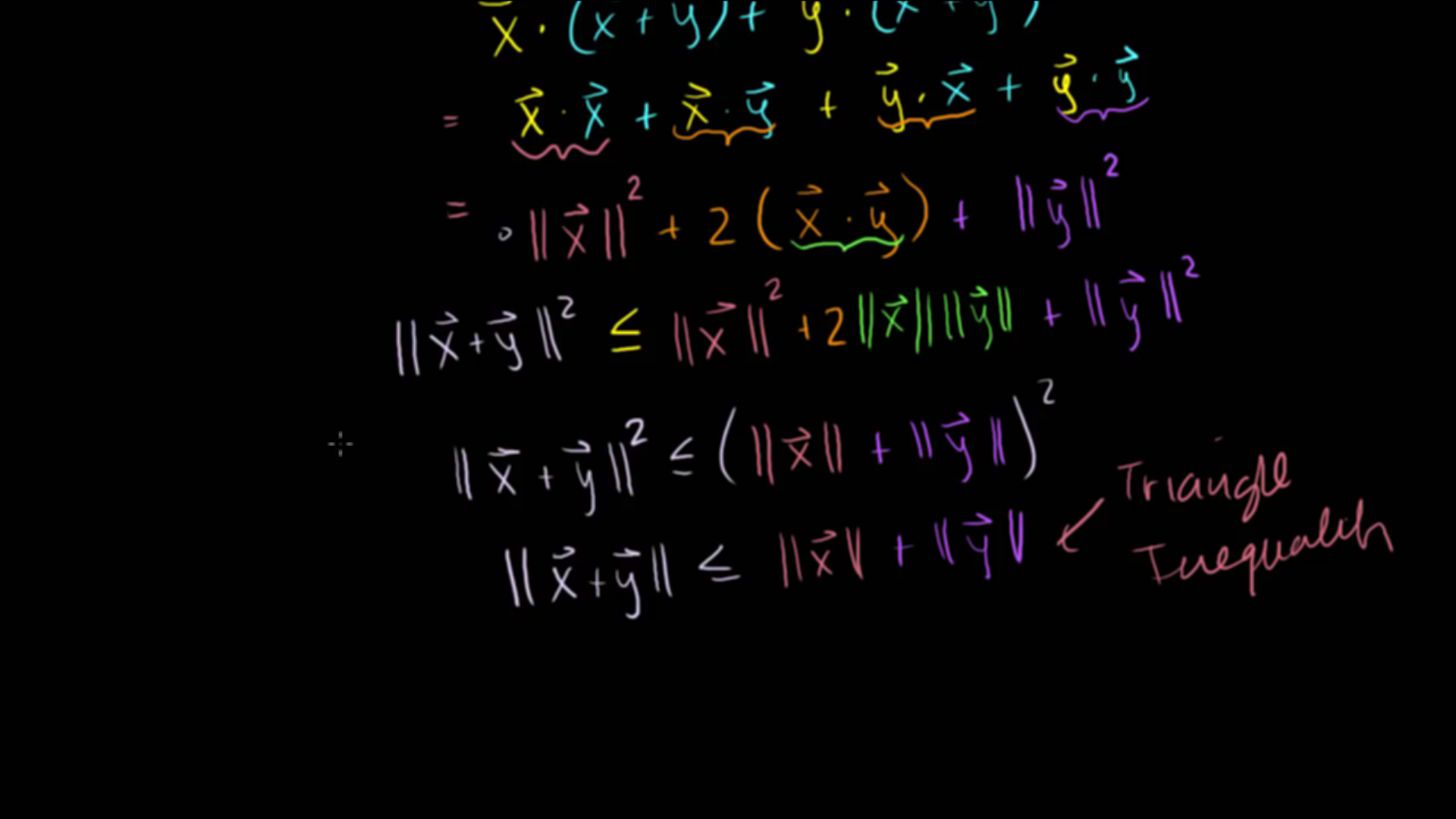
• 위 슬라이드에서 \(2(\vec{x} \cdot \vec{y})\) 은 코시 슈바르츠 부등식에 의하여 다음과 같이 정의될 수 있습니다.
  • 즉, \(2(\vec{x} \cdot \vec{y}) \le 2\Vert \vec{x} \Vert \Vert \vec{y} \Vert\) 입니다.
• 코시 슈바르츠 부등식을 이용하여 전개한 결과 \(\Vert \vec{x} + \vec{y} \Vert \le \Vert \vec{x} \Vert + \Vert \vec{y} \Vert\) 로 정리할 수 있습니다.
  • 위 식을 Triangle inequality 라고 합니다.

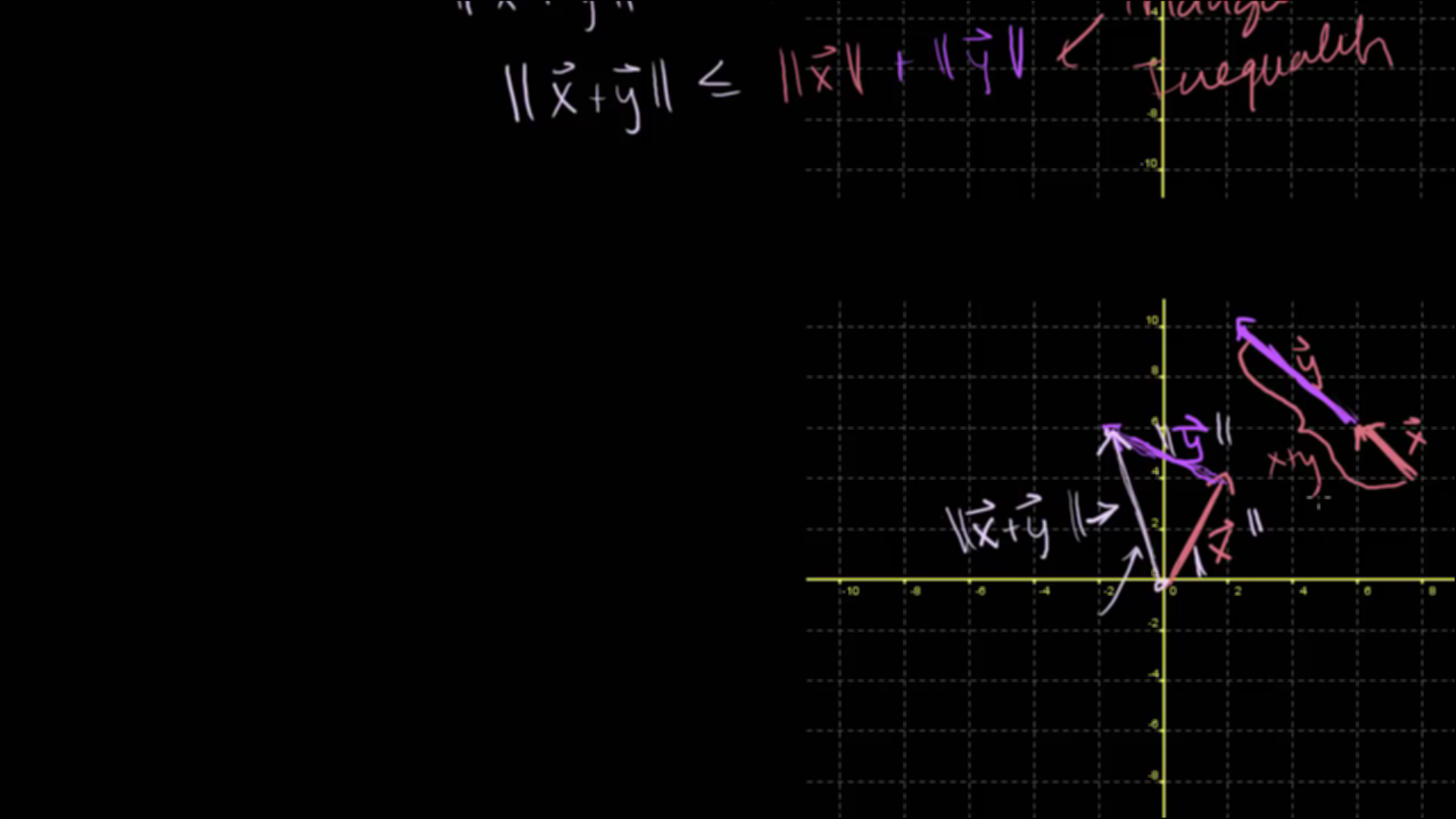
• Triangle inequality를 2차원 평면에 나타내 보겠습니다.
• 그림으로 나타내면 좀 더 명확하게 와닿습니다. 즉, 삼각형에서 두 선분의 합은 항상 대각선 보다 크거나 같다. 라는 뜻입니다.
• 어떤 경우에 Triangle inequality의 등호가 성립할까요?
  • 위 슬라이드의 그림처럼 \(\vec{x}\) 와 \(\vec{y}\) 가 동일 선상에 있을 때 입니다.

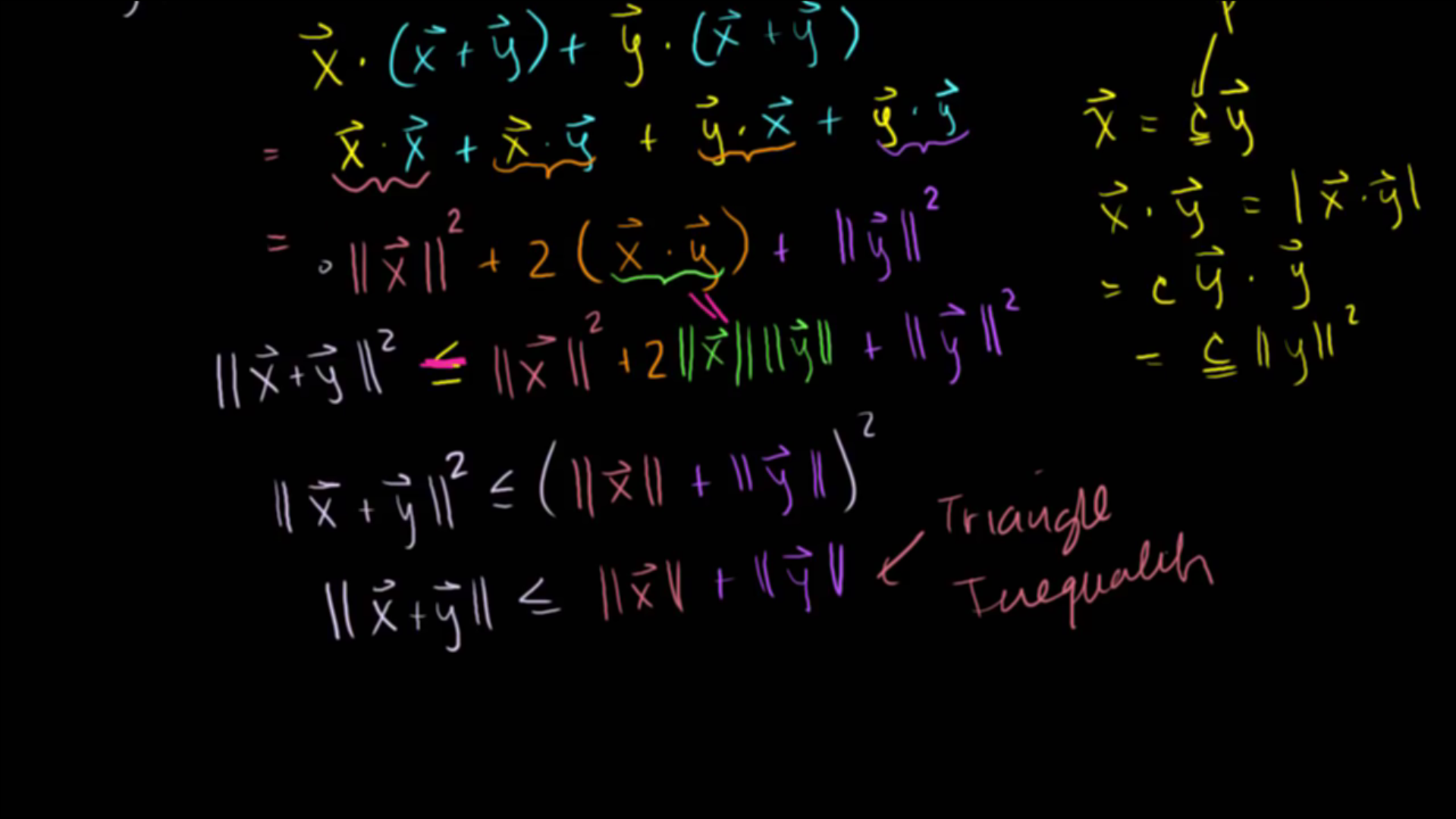
• 코시 슈바르츠 부등식에서도 등호가 성립할 때에는 \(\vec{x} = c\vec{y}\) 일 때 였습니다.
• Triangle inequality 또한 코시 슈바르츠 부등식을 이용한 정리이므로 \(\vec{x} = c\vec{y}\) 일 때 등호가 성립합니다.

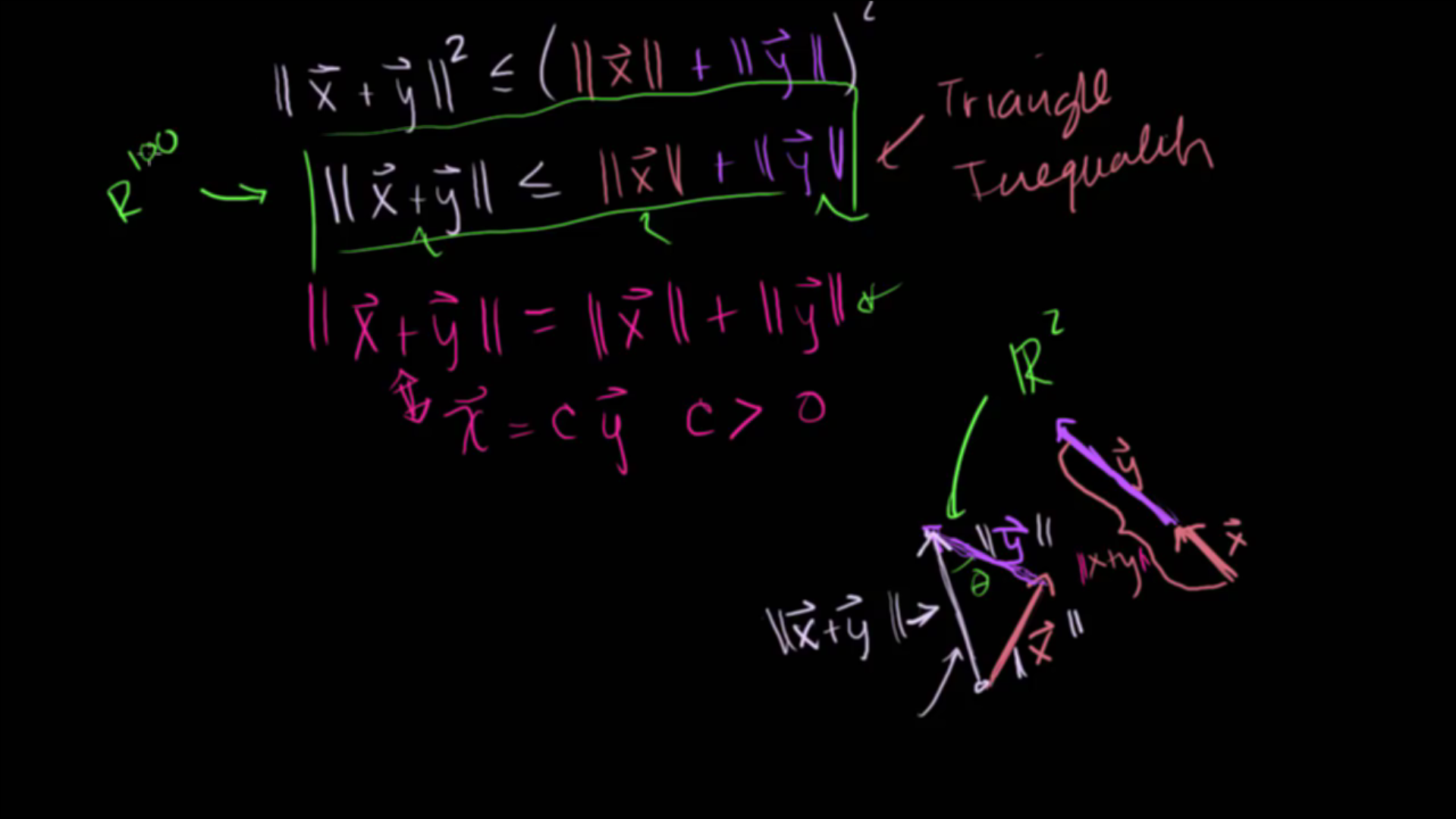
• 슬라이드에서 기하학적으로 벡터를 표시한 것은 \(\mathbb R^{2}\) 공간에서 였습니다.
• 하지만 Triangle inequality는 \(\mathbb R^{N}\) 공간에서도 성립 가능한다는 것에 의미가 있습니다.