Finding the size of a vector, its angle and projection

Inner product

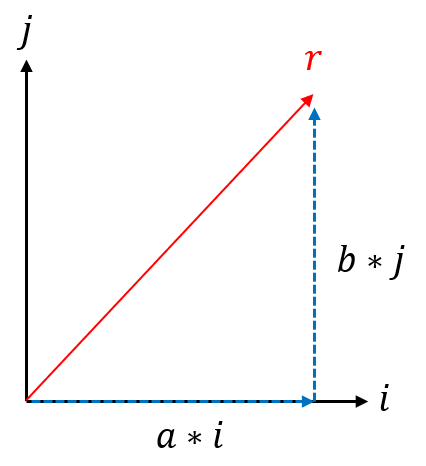
$Drawing$

unit vector는 각 축과 일치하는 방향으로 기본값인 1을 가지므로 어떤 vector는 unit vector를 이용하여 나타낼 수 있습니다.
위 그림에서 $r$ vector 또한 unit vector인 $i$와 $j$를 이용하여 나타낼 수 있습니다. 즉 $r$은 $i$ 벡터의 방향과 $j$ 벡터의 방향을 가지고 있다는 뜻입니다.
그러면 $r$은 $ai + bj$로 표현할 수 있습니다. vector 형태로 표현하면 $[a, b]$가 됩니다.
여기서 $\vert a \vert$는 무엇을 나타낼까요? 이것은 벡터의 크기를 나타냅니다. 따라서 $ai$는 unit vector를 a배 한 것이라고 말할 수 있습니다.
그러면 vector $r$의 크기는 어떻게 될까요? 이것은 피타고라스의 정리를 통하여 $\sqrt{a^{2} + b^{2}}$임을 알 수 있습니다.
- 물론 바로 뒤에서 쉽게 구하는 방법을 확인할 예정입니다.

그러면 unit vector를 이용하여 vector의 여러가지 기본 연산에 대하여 다루어보도록 하겠습니다.
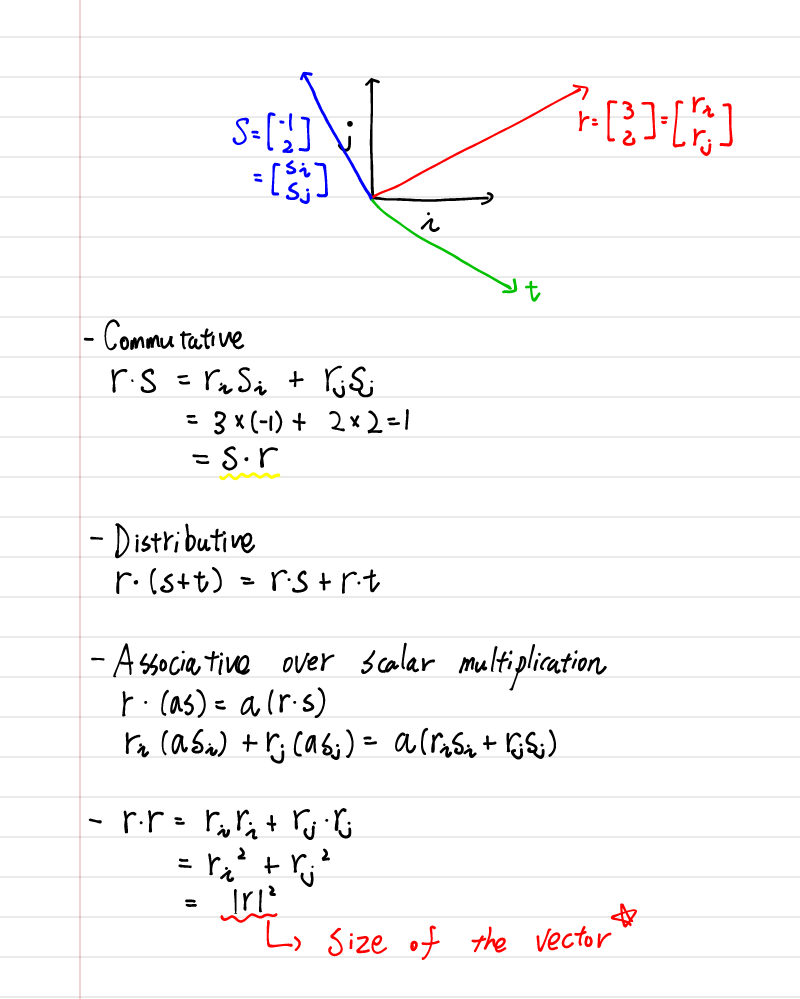
아래 이미지에서 다루는 것은 vector의 기본 연산 성질인 Commutative, Distributive, Associative 그리고 vector의 사이즈를 구하는 방법 입니다.

$Drawing$

이번에 다룰 내용은 Cosine Rule에 벡터를 적용하여 Cosine Similarity라는 식을 한번 전개해 보겠습니다.
여기서 사용할 성질은 바로 위에서 다룬 내용인 $r \cdot r = \vert r \vert^{2}$ 입니다.
여기서 $r$은 벡터이고 $\vert r \vert$는 벡터의 크기인 norm으로 스칼라 값입니다.
Cosine Rule에 사용되야 할 값은 벡터값이 아니라 스칼라 값이기 떄문에 norm이 대입 되지만 제곱의 형태이기 때문에 벡터 값으로 변환이 가능합니다. ( $r \cdot r = \vert r \vert^{2}$)

$Drawing$

이번에 알아 볼 내용은 projection입니다. projection에는 scalar projection과 vector projection이 있습니다.
scalar projection은 한 벡터에서 다른 벡터로 projection을 하였을 때 projection된 벡터의 시작점에서 projection된 지점까지의 거리(크기)를 나타냅니다.
반면 vector projection은 projection된 벡터의 시작점에서 projection된 지점까지의 거리만큼의 크기를 가지는 벡터를 나타냅니다.
그러면 두 벡터 $r, s$가 있고 벡터 $s$를 벡터 $r$에 projection 시킨다는 가정하에 scalar projection과 vector projection을 구하는 방법에 대하여 알아보겠습니다.

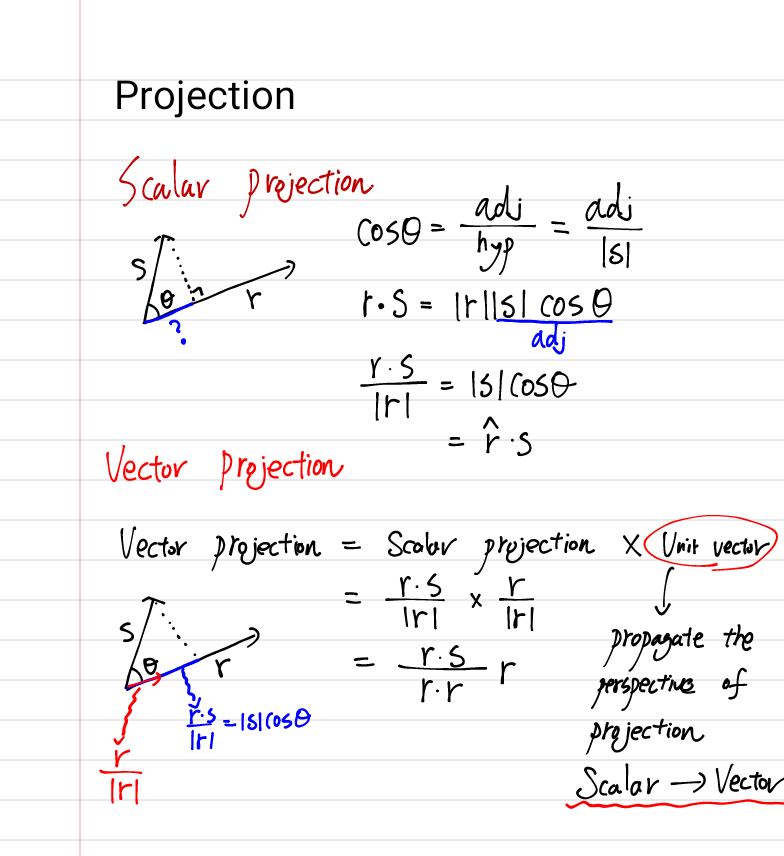
$Drawing$

위 계산 과정을 보면 scalar projection은 projection 된 벡터의 유닛 벡터($\hat{r}$ )와 projection한 벡터($s$)의 내적이 됨을 알 수 있습니다.
vector projection은 벡터이기 때문에 개념적으로 스칼라 값에 유닛 벡터를 곱하면 됩니다. 따라서 위 식과 같이 유도될 수 있습니다.