Basic Calculus

2019, Sep 27    

• 이 글은 Coursera의 Mathematics for Machine Learning: Multivariate Calculus 을 보고 정리한 내용입니다.

목차

• Rise Over Run

• Definition Of Derivative

• Product Rule

• Chain Rule

• 울프람 알파를 이용한 gradient 계산

Rise Over Run

• 먼저 Calculus의 간단한 정의를 내리면 어떤 함수가 입력 변수에 관하여 어떻게 변하는지를 나타낸 것이라고 말할 수 있습니다.

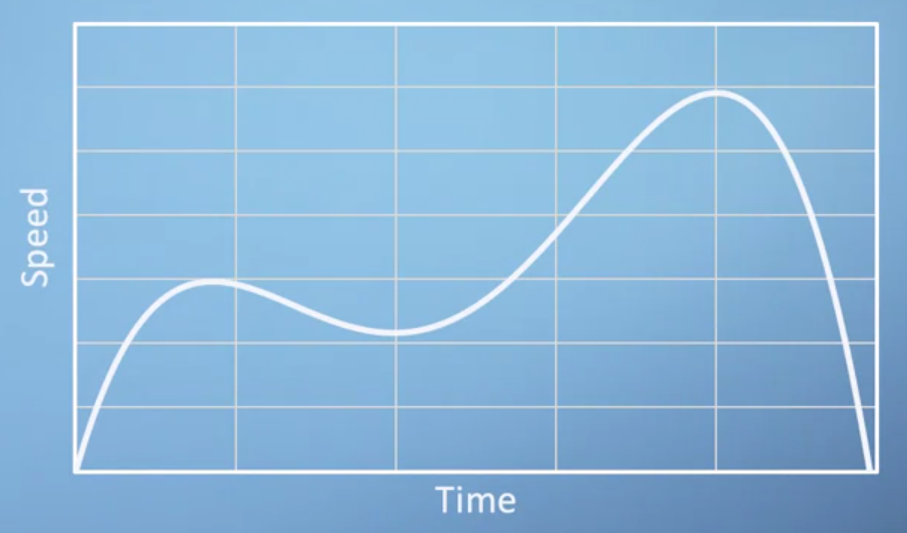
• 그러면 위 그림을 어떻게 해석하면 될까요? 입력 변수에 관하여 함수값이 어떻게 바뀌는지를 살피는 것이 목적입니다.
• 위 입력값은 X축인 시간입니다. 그러면 시간에 따라 함수값인 Speed가 어떻게 바뀌는지 살펴보면 시간에 따라 다양하게 변화하고 있습니다.
• 이 때의 변화량을 알고 싶습니다. 변화량을 확인하고 싶으면 곡선에 접하는 선의 기울기를 이용하여 확인할 수 있습니다.

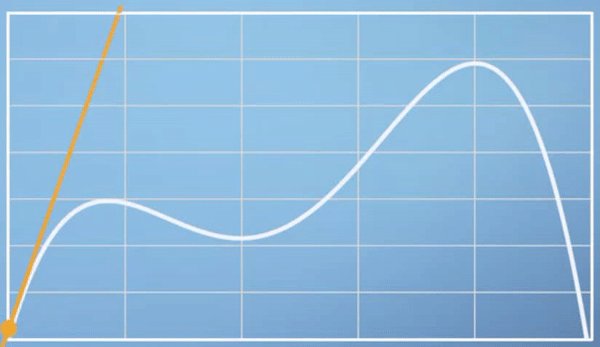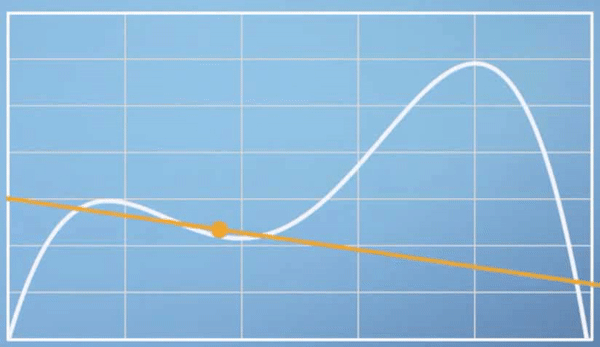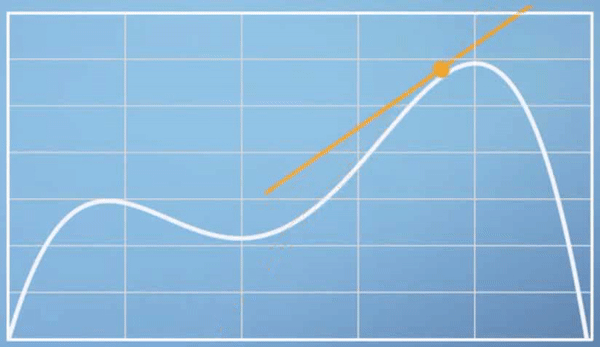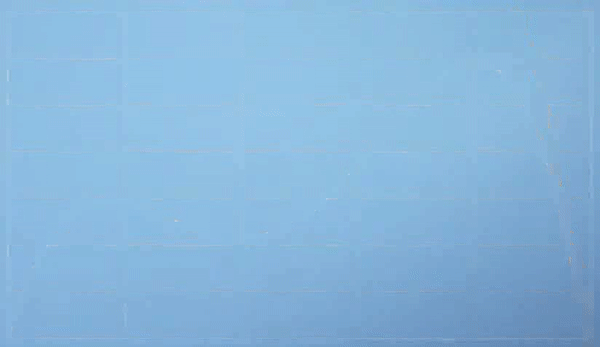
• 위 이미지를 보면 입력값인 시간에 따라서 속도가 바뀌고 그 순간 순간의 변화가 얼만큼인지에 해당하는 변화율 또한 나타낼 수 있음을 알 수 있습니다.
• 변화율은 속도가 증가할때는 양의 방향의 직선을 나타내다가 속도가 정체하면 수평방향의 직선 그리고 속도가 감소하면 음의 방향의 직선 모양을 가집니다.

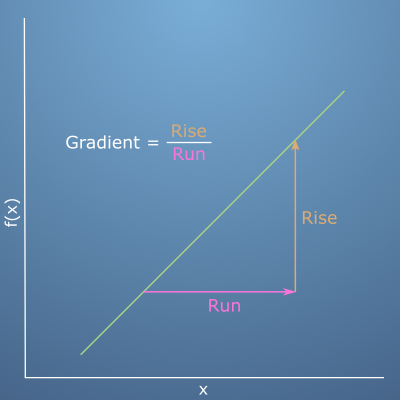
• 앞에서 계속 다룬 gradient 라는 개념은 변화율을 뜻하는 것이었고 이것은 Rise Over Run이라고 표현하기도 합니다.
• 위 그림을 보면 Run은 입력값 x의 증감양을 나타내고 Rise는 함수값 f(x)의 증감양을 나타냅니다. 따라서 입력값 대비 함수값의 변화양이 gradient가 됩니다.

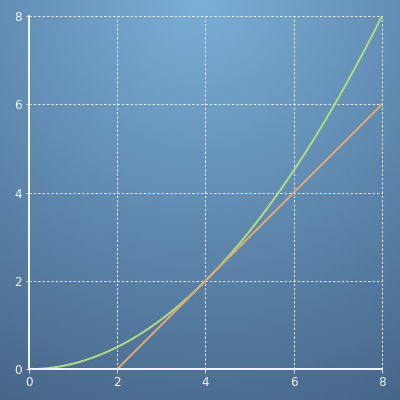
• 예를 들어 위와 같은 경우에 입력이 4인 지점의 gradient를 보면 run인 입력값의 변화량은 6 - 2 = 4이고 rise의 변화량은 4 - 0 = 4이므로 gradient는 1이 됩니다.

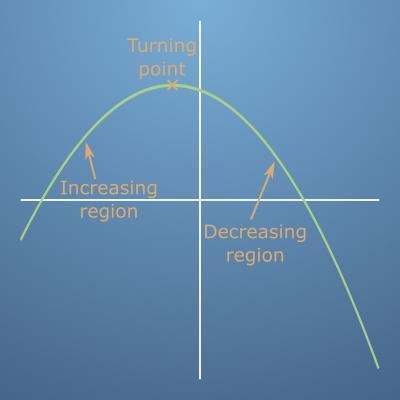
• 위와 같은 그래프에서 gradient만을 그래프로 표현하면 어떻게 될까요?
• 위 그래프의 gradient의 추이를 보면 입력값이 증가할수록 gradient가 점점 감소하고 있습니다.
• 그리고 gradient는 양의 값부터 시작해서 음의 값으로 변하고 있습니다.
• 또한 gradient가 0이되는 지점 즉, turning point는 한 곳에만 있음을 알 수 있습니다.

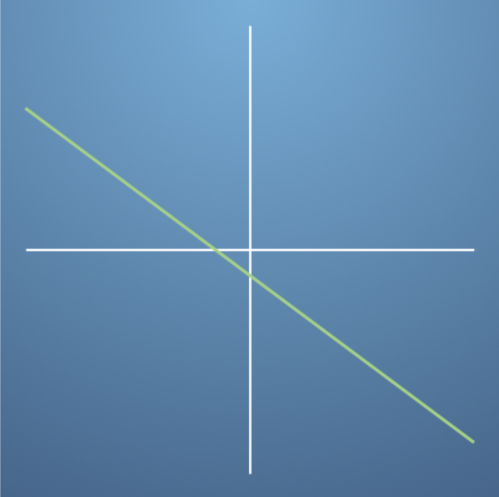
• 따라서 그래프를 표현하면 위와 같이 표현할 수 있습니다.
• 앞에서 살펴본 바와 같이 입력값이 증가할수록 gradient가 감소하고 turning point 즉, gradient = 0인 지점은 한번 있습니다.

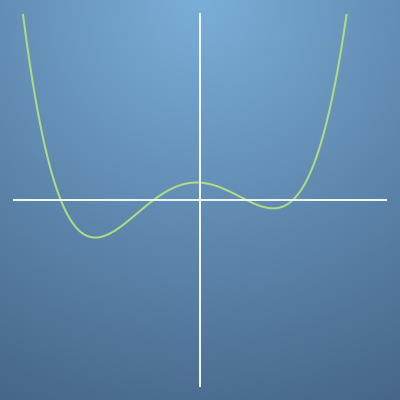
• 만약 위와 같은 그래프의 gradient를 표현하면 어떻게 될까요?

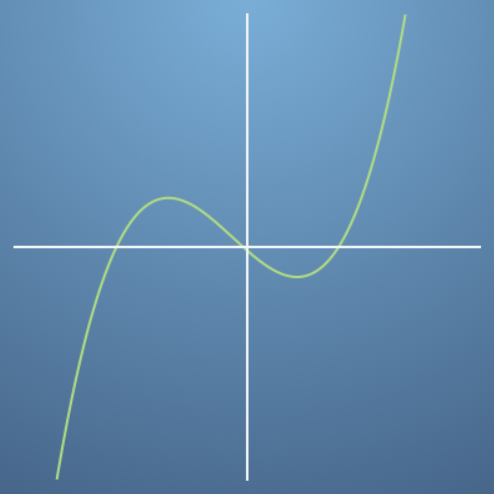
• 위와 같이 gradient를 표현할 수 있습니다.
• gradient는 음의 값부터 시작해서 양의 값으로 다시 음의 값으로 변했다가 최종 양의 값이 됩니다.
• 이 때 turning point는 3번 생깁니다.

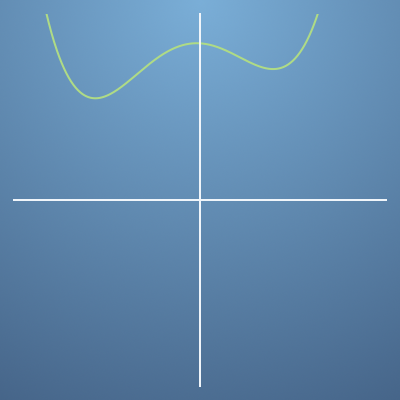
• 또 다른 예시를 살펴보겠습니다. 이번 그래프는 앞의 그래프에 비교해서 y축으로 평행이동한 상태입니다.
• 이 경우의 gradient는 어떻게 될까요?

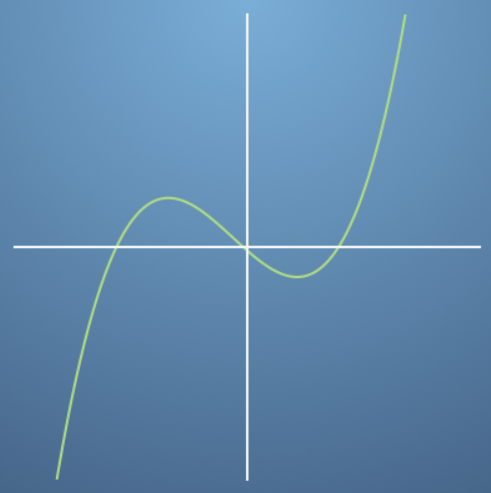
• gradient는 변화량과 관계가 있지 실제 함수값이 가지는 값의 크기와는 관련이 없습니다. 변화량만 같다면 동일한 패턴의 gradient그래프를 그릴 수 있습니다.

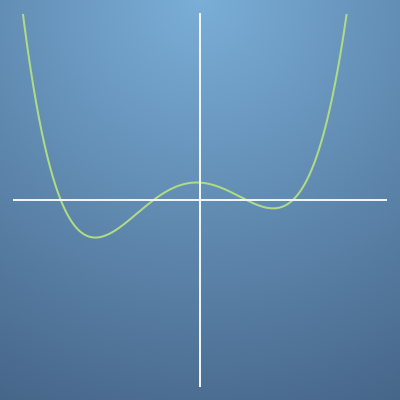
• 그러면 반대로 위와 같은 gradient 그래프가 있으면 어떤 형태의 그래프에서 도출될 수 있을까요?
• 위 gradient를 보면 먼저 4번의 0 값을 가지기 때문에 4번의 turnning point를 가집니다.
• 그리고 gradient가 범위에 따라 음의 값인지 양의 값인지를 확인하여 살펴보면 다음 그래프를 그릴 수 있습니다.

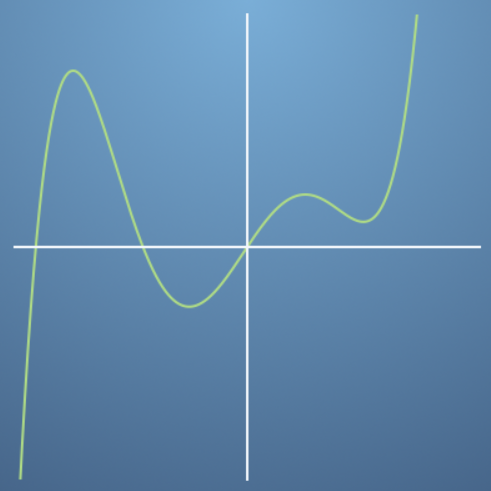
• 예를 들면 위와 같이 4번의 변곡점을 가지는 그래프를 그릴 수 있습니다.

Definition Of Derivative

• 그러면 앞에서 배운 개념을 좀 더 formal한 방법으로 한번 다루어 보겠습니다.
• 앞에서 다룬 gradient = Rise Over Run을 생각해보면서 좀 더 정교한 식으로 한번 나타내 보려고 합니다.

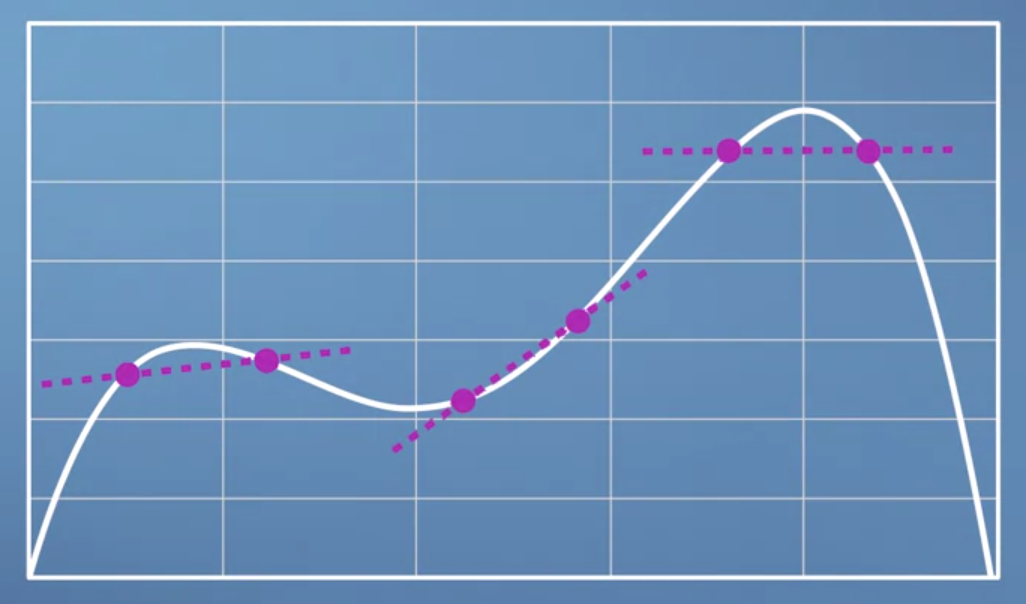
• 먼저 gradient는 순간 순간마다 다릅니다. 즉, 위 그림과 같이 어떤 점을 잡느냐에 따라서 gradient는 다릅니다.

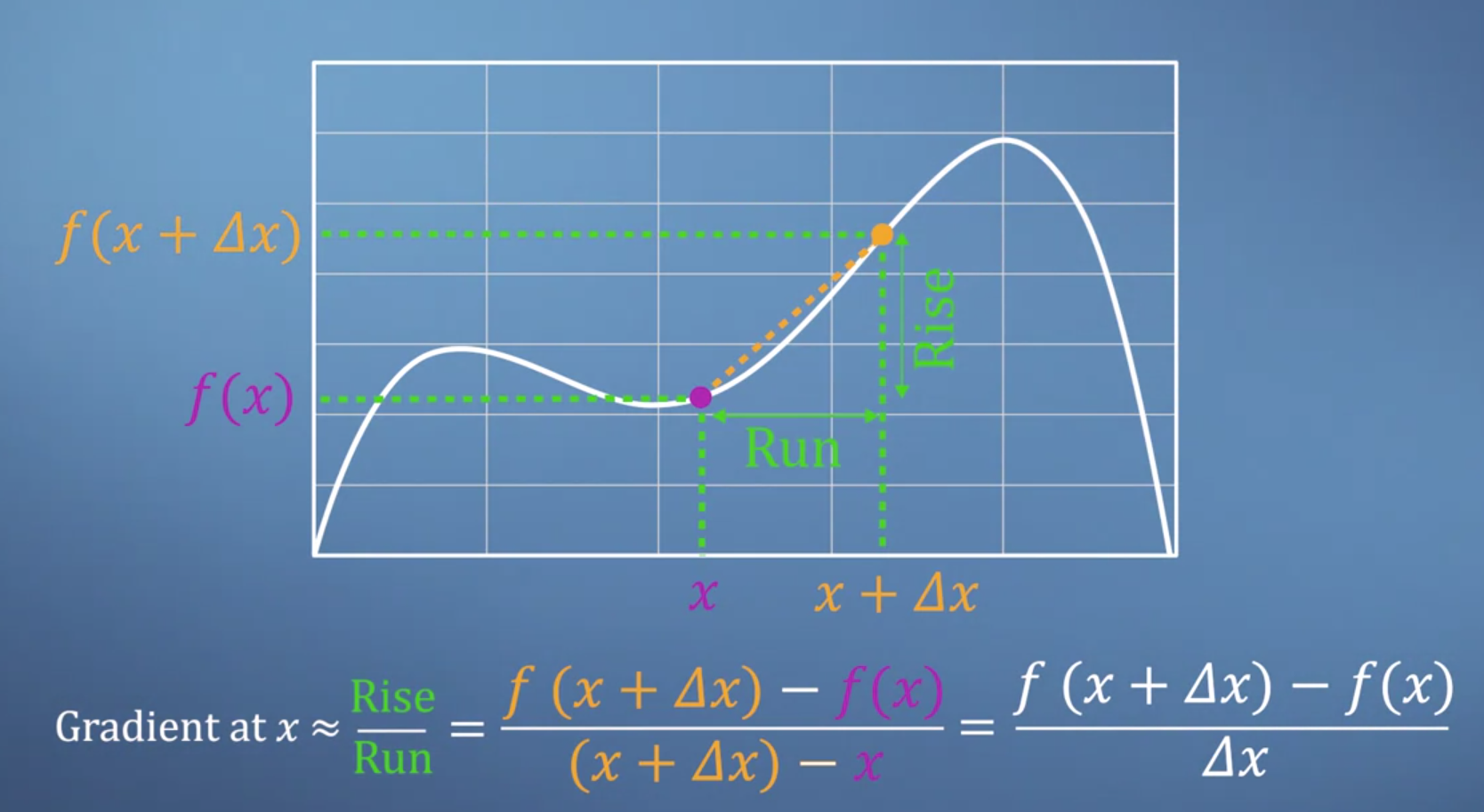
• 이런 gradient를 계산하기 위해서는 Rise Over Run을 좀 더 수식적으로 나타낼 필요가 있습니다.
• 먼저 수학에서 사용하는 기호인 \(\Delta\)는 작은 변화량을 나타낼 때 사용합니다.
• Run에 해당하는 가로축의 변화량을 보면 \(\Delta x\) 만큼 변화하였고 Rise인 세로축을 보면 \(f(x + \Delta x) - f(x)\) 만큼 변한것을 확인할 수 있습니다.

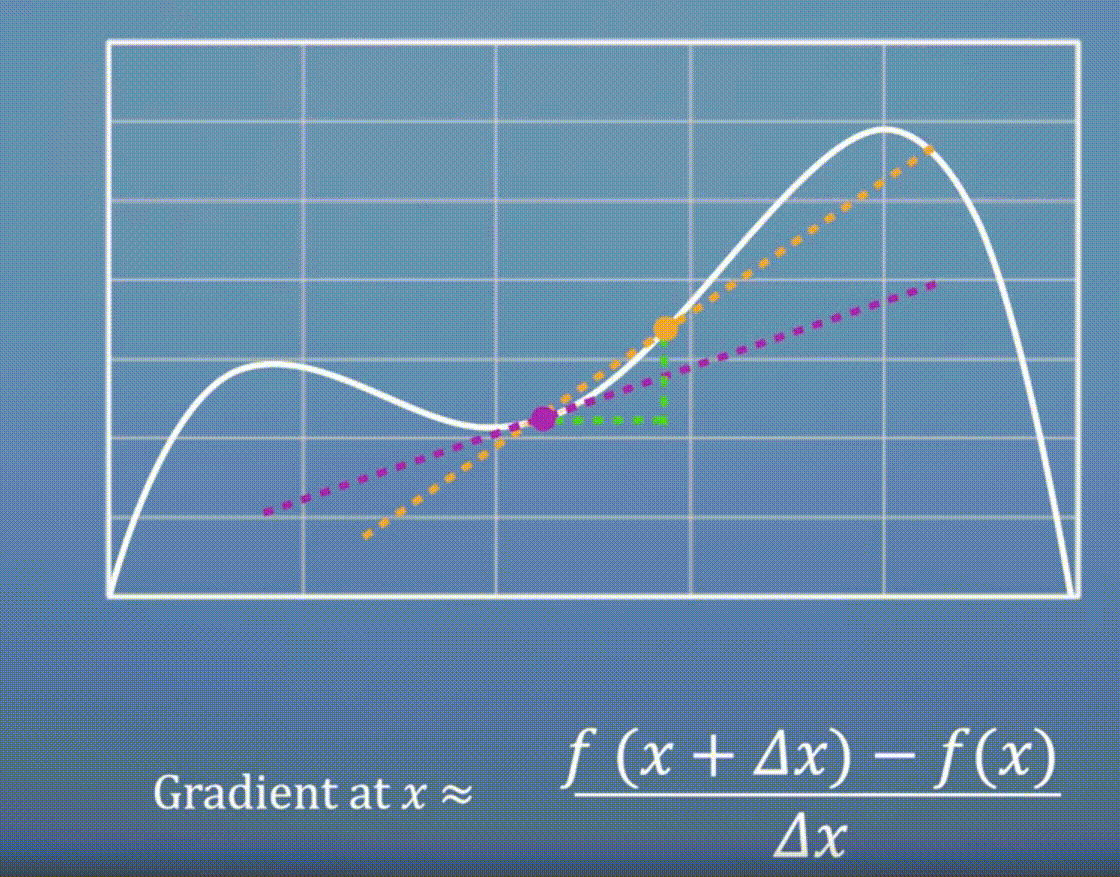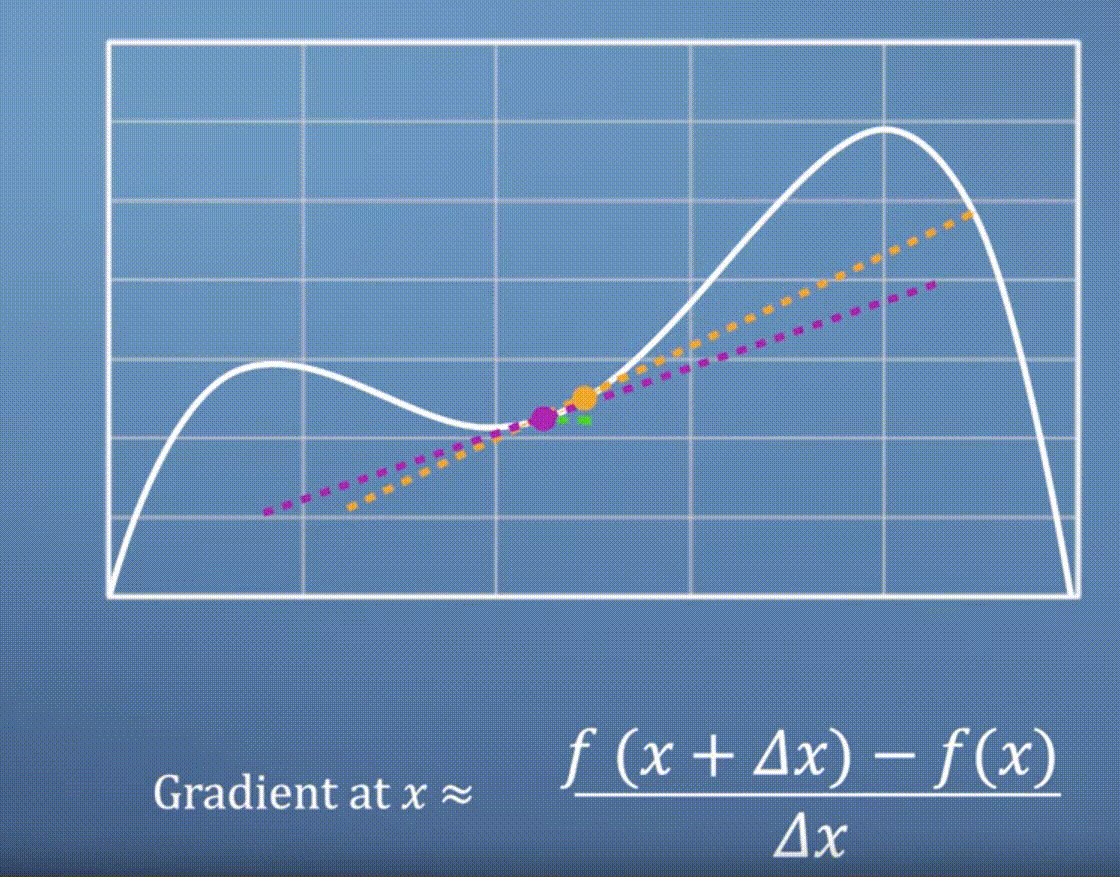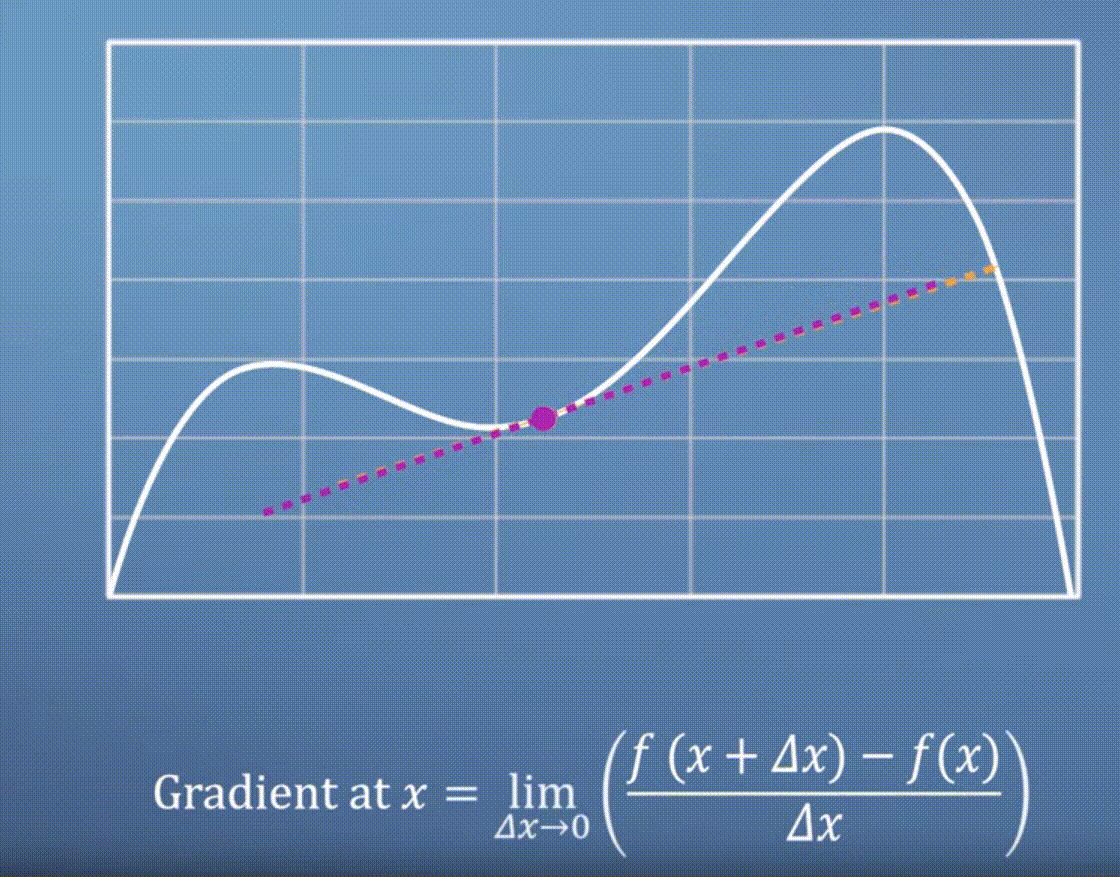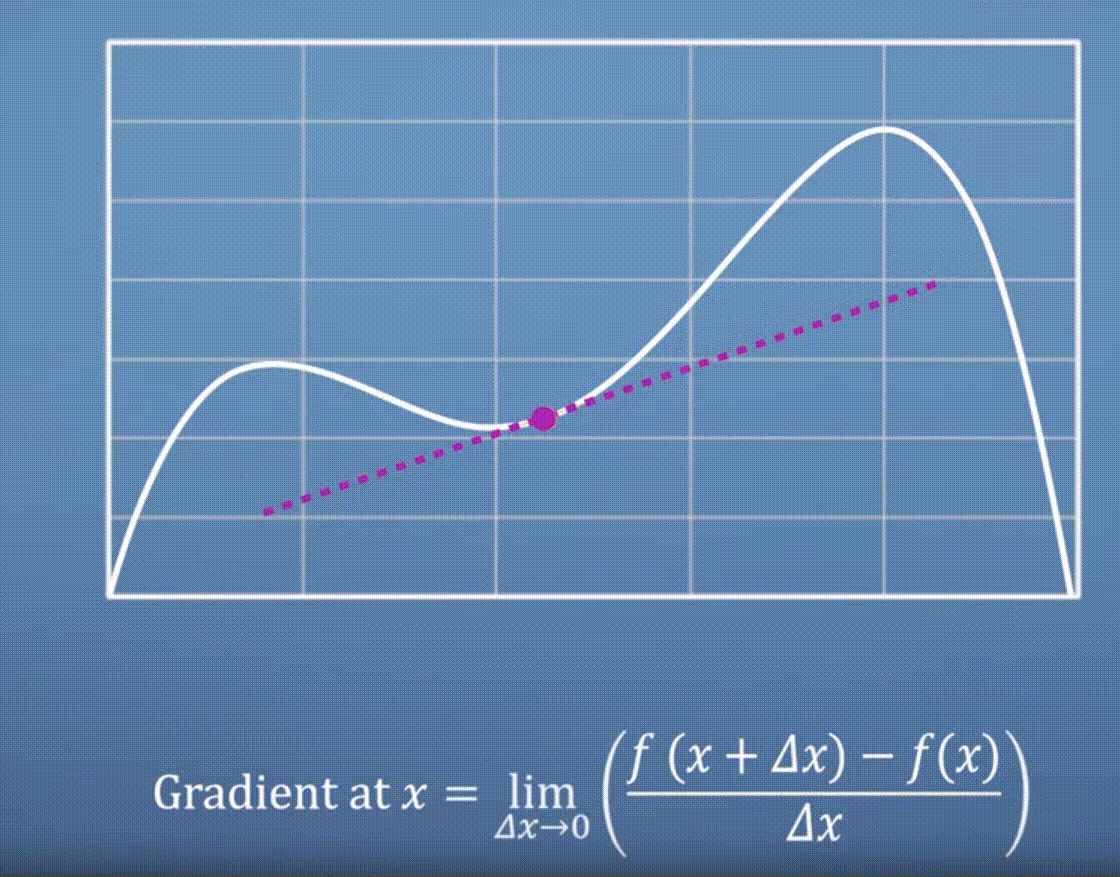
• 이 때 Run에 해당하는 입력값의 변화량 \(\Delta x\)를 줄이면 줄일수록 더 나은 gradient 근사값을 찾을 수 있습니다.

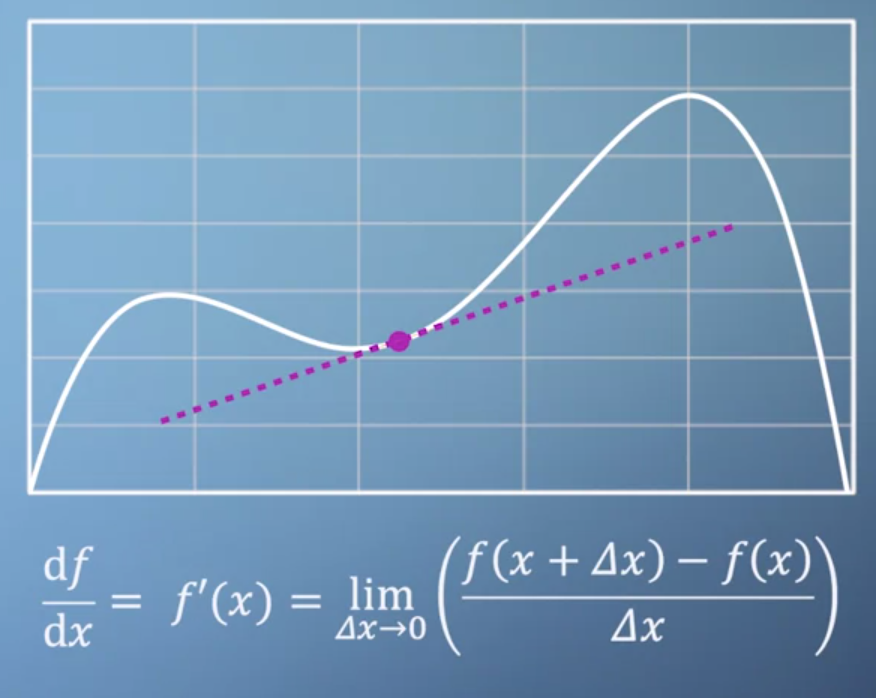
• 이 표현 방법을 위와 같이 limitation을 이용하여 식으로 나타낼 수 있습니다.
• gradient라는 용어 대신 식으로 \(\frac{df}{dx}\)로 나타내기도 하고 \(f'(x)\)로 나타내기도 합니다.
• 다시 한번 정리해 보겠습니다. gradient를 나타내는 식은 다음과 같습니다.

• \[f'(x) = \lim_{\Delta x \to 0}\Bigl( \frac{ f(x + \Delta x) - f(x) }{\Delta x} \Bigr)\]

• 이 식을 이용하여 \(f(x) = 3x + 2\)일 때를 예로 한번 gradient를 살펴보겠습니다.

• \[f'(x) = \lim_{\Delta x \to 0} = \Bigl( \frac{ 3(x + \Delta x) + 2 - (3x + 2) }{\Delta x} \Bigr) = 3\]

• 또 다른 예로 \(f(x) = 5x^{2}\) 일 때를 살펴보겠습니다.

• \[f'(x) = \lim_{\Delta x \to 0}\Bigl( \frac{ 5(x + \Delta x)^{2} - 5x^{2} }{\Delta x} \Bigr) = \lim_{\Delta x \to 0}\Bigl( \frac{5x^{2} + 10x\Delta x + 5(\Delta x)^{2} - 5x^{2} }{\Delta x} \Bigr) = \lim_{\Delta x \to 0}(10x + 5\Delta x) = 10x\]

• 위와 같이 \(\lim_{\Delta x \to 0}(10x + 5\Delta x) = 10x\)식을 전개할 때 사용할 수 있는 법칙이 Sum Rule입니다.

• \[\frac{d}{dx} (f(x) + g(x)) = \frac{df(x)}{dx} + \frac{dg(x)}{dx} \ \cdots \text{Sum Rule}\]

• 그리고 매번 gradient를 구할 때, 이 과정을 반복하기는 번거로우므로 다음 Power Rule을 대신 사용하겠습니다.

• \[f(x) = ax^{b}, f'(x) = abx^{b-1} \ \cdots \text{Power Rule}\]

• 그러면 Sum Rule과 Power Rule을 이용하여 몇가지 예제를 다루어 보도록 하겠습니다.
• 다루어 볼 예제는 \(f(x) = 1/x, e^{x}, sin(x), cos(x)\) 입니다.
• 먼저 \(f(x) = 1/x\) 부터 다루어보겠습니다. gradient의 정의에 따라서 식을 전개해 보면 다음과 같습니다.

• \[f'(x) = \lim_{x \to 0} \Biggl( \frac{ \frac{1}{x + \Delta x} - \frac{1}{x} }{\Delta x} \Biggr) = \lim_{x \to 0} \Bigl( -\frac{1}{x^{2}+x\Delta x} \Bigr) = -\frac{1}{x^{2}}\]

• 따라서 위 결과를 그래프로 나타내면 다음과 같습니다.

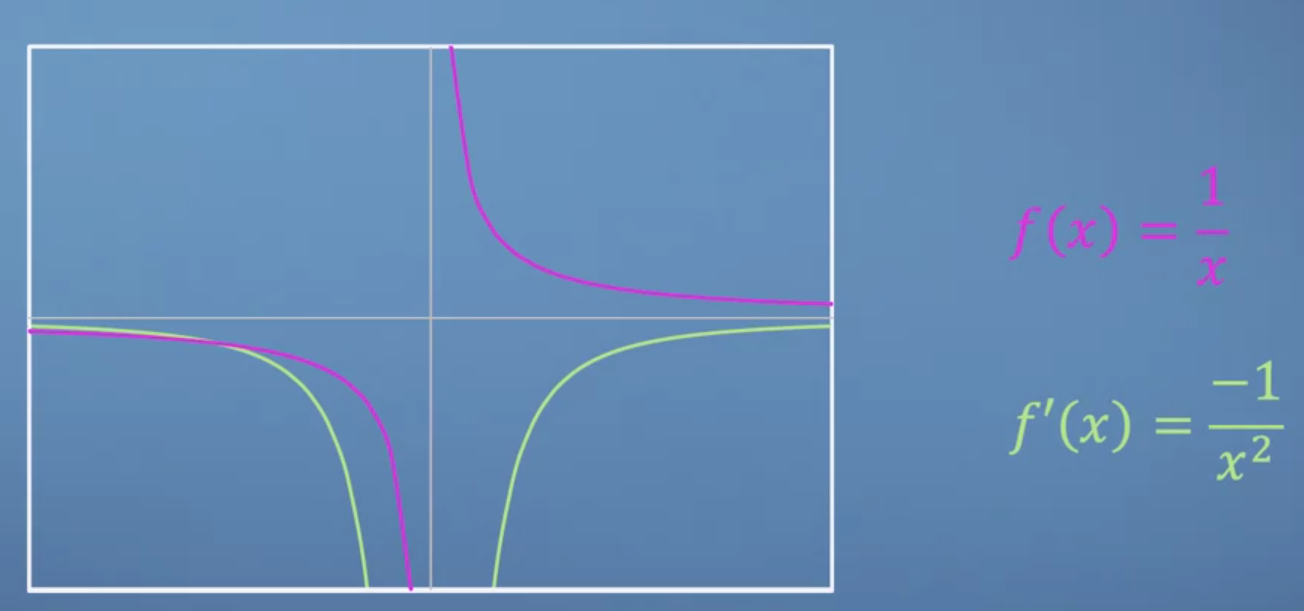
• 그 다음에 다뤄볼 \(f(x) = e^{x}\) 의 경우에는 Euler가 발견한 특수한 형태의 함수입니다.
• 이 함수의 경우 gradient의 값이 원래 값과 같습니다. 즉, \(f(x) = e^{x}, \ f'(x) = e^{x}, \ f^{2}(x) = e^{x}, \ f^{n}(x) = e^{x}\) 가 됩니다.
• 즉, 이 뜻은 \(f(x) = e^{x}\)의 경우 변화율 자체가 \(e^{x}\)라는 뜻입니다. 이 특수한 성질 때문에 이 함수는 미분/적분에서 상당히 많이 사용됩니다.

• 그 다음으로 다루어 볼 함수는 \(sin(x), cos(x)\) 입니다.
• 이 두 함수도 특이한 성질을 가지게 되는데 다음 그래프를 먼저 살펴보겠습니다.

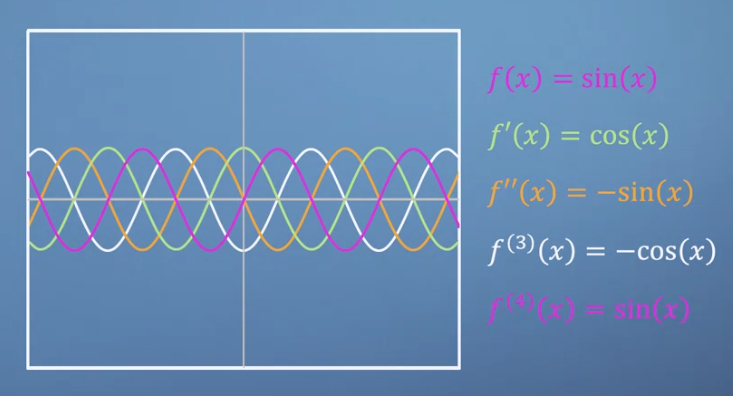
• 위와 같이 \(sin(x)\)와 \(cos(x)\)의 gradient는 서로 관계를 가지게 됩니다. 즉 \(sin(x)\)의 gradient는 \(cos(x)\)가 되고 \(cos(x)\)의 gradient는 \(-sin(x)\)가 됩니다.
• 이렇게 되는 이유는 실질적인 \(sin(x)\)와 \(cos(x)\)의 gradient를 계산해 본 결과 확인할 수도 있지만 오일러 공식에 의한 삼각함수와 지수함수의 관계를 통해서도 확인해 볼 수 있습니다.
  • 참조 자료: https://suhak.tistory.com/163

• \[\text{Euler formula : } e^{ix} = \cos{x} + i*\sin{x}\]

• \[\sin{x} = \frac{ e^{ix} - e^{ix} }{2i}\]
• \[\cos{x} = \frac{ e^{ix} + e^{ix} }{2i}\]

Product Rule

• 이번에 다루어 볼 것은 gradient를 계산할 때 자주 사용되는 방법 중 하나인 Pruduct Rule 입니다.
• Product Rule은 함수가 곱해진 상태에서 미분을 하였을 때의 식을 전개하는 방법입니다. 예를 들면 \(f(x)g(x) = e^{x}sin(x)\)와 같이 두 식이 곱해진 경우 입니다.
• 개념을 쉽게 이해하기 위해서 시각적으로 한번 살펴보겠습니다. 먼저 definition of derivative에서 다룬 식을 다시 적어보면 다음과 같습니다.

• \[f'(x) = \lim_{x \to 0} \Bigl( \frac{f(x + \Delta x) - f(x) }{\Delta x} \Bigr)\]

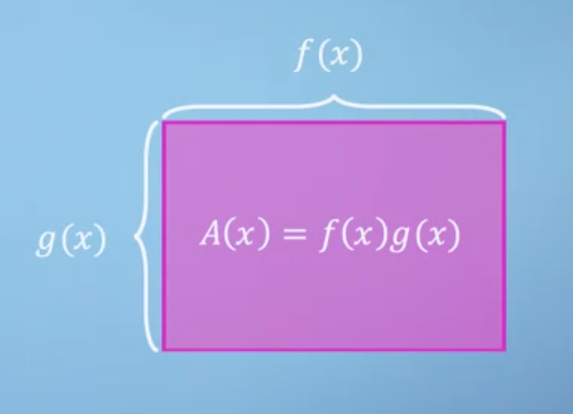
• 만약 위와 같이 \(A(x) = f(x)g(x)\)라면 그 값을 면적으로 표현해 볼 수 있습니다.

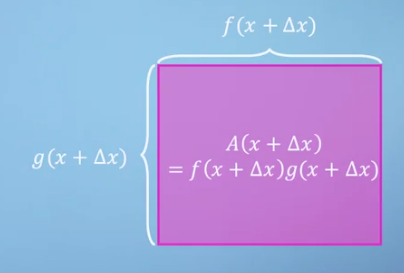
• 이 때, \(x\)가 \(\Delta x\) 만큼 변화가 생긴다면 위 그림과 같이 넓이가 증가합니다.

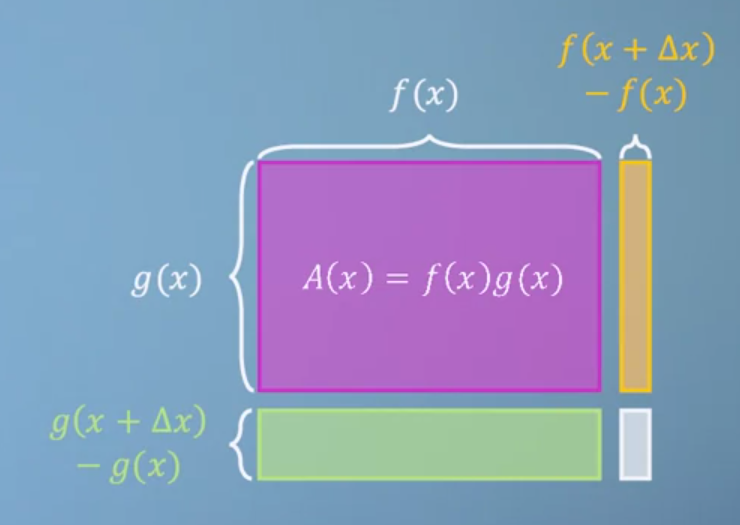
• 이 때 \(A(x + \Delta x)\)에서 증가분 만큼 따로 표시해보겠습니다. 즉, 연두색, 주황색, 회색 영역만큼의 값이 \(A(\Delta x)\)의 값입니다.

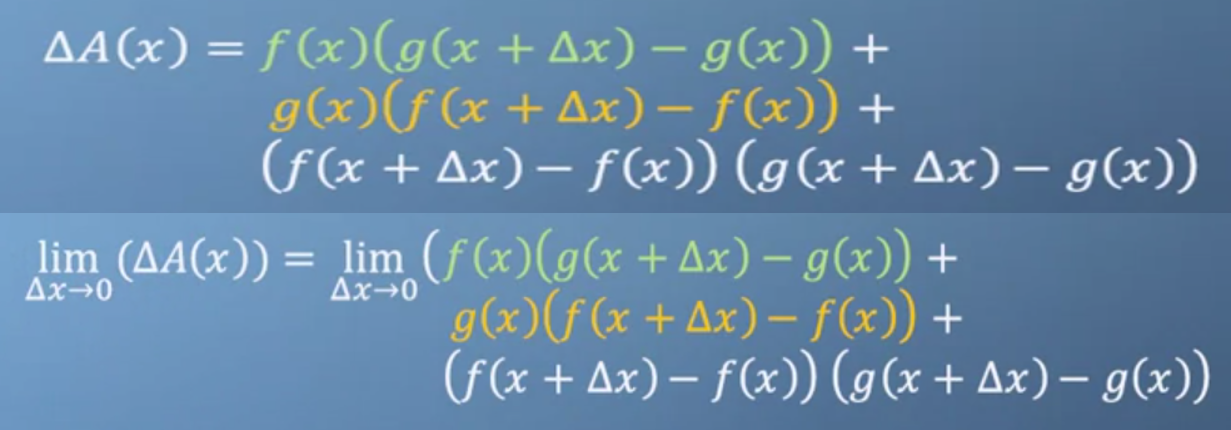
• 이 영역을 식으로 나타내면 위와 같이 나타낼 수 있습니다. 증가분에 대응하도록 식을 색으로 표현하였습니다.
• 여기서 \(\lim_{\Delta x \to 0}\) 으로 인하여 \(\Delta x\)는 0으로 수렴하게 되므로 회색 영역의 값은 무시할 수 있게 됩니다.
• 여기서 gradient를 구해보겠습니다.

• \[\begin{split} \lim_{\Delta x \to 0} \Bigl( \frac{ \Delta A(x) }{ \Delta x } \Bigr) &= \lim_{\Delta x \to 0} \Bigl( \frac{ f(x)( g(x + \Delta x) - g(x) ) + g(x)( f(x + \Delta x) - f(x) ) }{ \Delta x } \Bigr) \\ &= \lim_{\Delta x \to 0} \Bigl( \frac{ f(x)( g(x + \Delta x) - g(x) ) + g(x) }{ \Delta x } + \frac{ g(x)( f(x + \Delta x) - f(x) ) }{ \Delta x } \Bigr) \\ &= \lim_{\Delta x \to 0} \Bigl( f(x) \frac{ ( g(x + \Delta x) - g(x) ) + g(x) }{ \Delta x } + g(x) \frac{ ( f(x + \Delta x) - f(x) ) }{ \Delta x } \Bigr) \\ &= \lim_{\Delta x \to 0} ( f(x)g'(x) + g(x)f'(x)) \end{split}\]

• \[A'(x) = f(x)g'(x) + f'(x)g(x)\]

• 다시 정리하면 Product Rule은 다음과 같습니다.

• \[\text{if} \ \ A(x) = f(x)g(x), \ \ \text{then} \ \ A'(x) = f(x)g'(x) + f'(x)g(x)\]

• 같은 원리로 식을 확장해 보겠습니다. \(u(x) = f(x)g(x)h(x)\) 라고 하면 definition of gradient 에 따라 식을 전개하면 결과는 다음과 같습니다.

• \[u'(x) = f'(x)g(x)h(x) + f(x)g'(x)h(x) + f(x)g(x)h'(x)\]

Chain Rule

• 이번에 다루어 볼 내용은 Chain Rule 입니다. 이 방법은 gradient를 구할 때 상당히 중요한 방법입니다.
• 이번 내용을 다룰 때, 좀 더 친숙하게 다가가기 위하여 강의에서는 happy와 pizza 라는 함수를 도입하였습니다.
• 함수 \(h(x)\)는 얼마나 happy한 지에 대한 함수이고 \(p(x)\)는 얼마나 많은 피자를 먹었는 지 에 대한 함수 입니다.
• 따라서 \(h(p(m))\) 이라는 함수는 money라는 인풋 \(m\)을 이용해서 피자를 먹으면 얼마나 행복해질 지에 대한 함수입니다.
• 즉, money와 happiness의 관계를 pizza를 통하여 구하는 것입니다.

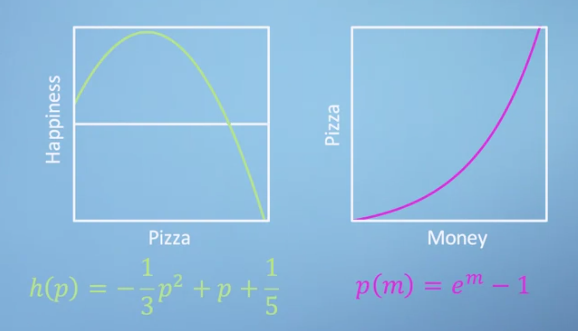
• 만약 \(h(x), p(x)\)가 위 그래프를 따른다고 가정해 보겠습니다.
• 피자의 경우 한판, 두판을 먹을 때에는 효용이 있다가 너무 많이 먹으면 오히려 배가 불러서 불쾌해 집니다. 따라서 피자의 수에 따른 행복감의 그래프는 왼쪽 그래프 처럼 그려질 수 있습니다.
• 피자와 돈의 그래프는 돈이 증가할 수록 구매 가능한 피자의 수는 기하급수적으로 증가할 수 있다는 것을 표현하였습니다. 규모의 경제가 적용되었습니다.
• 위 식을 이용하여 \(h(p(m))\)을 구해보겠습니다.

• \[h(p(m)) = - \frac{1}{3}(e^{m} -1)^{2} + (e^{m} -1) + \frac{1}{5}\]

• 위 식을 \(m\)에 대하여 미분을 하면 다음과 같습니다.

• \[\frac{dh}{dm} = \frac{1}{3} e^{m} (5 - 2e^{m})\]

• 위 식이 전개된 순서를 보면 다음과 같습니다.

• \[\frac{\text{d}h}{\text{d}p}\frac{\text{d}p}{\text{d}m} = \frac{\text{d}h}{\text{d}m}\]

• 여기서 최종적으로는 입력값에 대한 최종 함수의 변화율을 관찰하는 것이지만 계산 과정은 중간에 소거되는 부분을 통하여 계산됩니다.
• 이 관계를 chain of derivative relationship 이라고 하고 간단히 Chain Rule이라고 합니다. 정리하면 다음과 같습니다.

• \[\text{if} \ \ h = h(p) \ \ \text{and} \ \ p = p(m) \\ \text{then}, \frac{\text{d}h}{dm} = \frac{\text{d}h}{\text{d}p} \times \frac{\text{d}p}{\text{d}m}\]

• 이 관계를 앞의 식에 대입해 보겠습니다.

• \[h(p) = -\frac{1}{3}p^{2} + p + \frac{1}{5}, \ \ p(m) = e^{m} -1\]

• \[\frac{\text{d}h}{\text{d}p} = 1 - \frac{2}{3}p, \ \ \frac{\text{d}p}{\text{d}m} = e^{m}\]

• \[\frac{\text{d}h}{dp}\frac{dp}{dm} = (1 - \frac{2}{3}p)e^{m} = (1 - \frac{2}{3}(e^{m} -1))e^{m}\]

• \[\frac{\text{d}h}{\text{d}m} = \frac{1}{3}e^{m}(5 - 2e^{m})\]

울프람 알파를 이용한 gradient 계산

• 이번에 다루어 볼 예제는 약간 계산이 필요한 예제입니다.
• 앞에서 배운 Sum, Power, Product Chain Rule을 모두 이용하여 한번 식을 전개해보고 울프람 알파를 통하여 간단하게 계산하는 방법도 익혀보겠습니다.
• 다음 식을 한번 미분해 보겠습니다.

• \[f(x) = \frac{ \sin{2x^{5} + 3x} }{ e^{7x} } = \sin{2x^{5} + 3x}e^{-7x}\]

• \[g(x) = \sin{2x^{5} + 3x}\]

• \[g(u) = \sin{u}, \ \to \ g'(u) = \cos{u}\]

• \[u(x) = 2x^{5} + 3x \ \to \ u'(x) = 10x^{4} + 3\]

• \[\frac{\text{d}g}{\text{d}x} = \frac{\text{d}g}{\text{d}u} \frac{\text{d}u}{\text{d}x} = \cos{u}(10x^{4} + 3) = \cos{2x^{5} + 3x}(10x^{4} + 3)\]

• \[h(v) = e^{v} \ \to \ h'(v) = e^{v}\]

• \[v(x) = -7x \ \to \ v'(x) = -7\]

• \[\frac{\text{d}h}{\text{d}x} = \frac{\text{d}h}{\text{d}v} \frac{\text{d}v}{\text{d}x} = -7e^{-7x}\]

• \[g'(x) = cos(2x^{5} + 3x)(10x^{4} + 3) , \ \ h'(x) = -7e^{-7x}\]

• \[\frac{\text{d}f}{x} = \frac{\text{d}g}{\text{d}x}h + g\frac{\text{d}h}{\text{d}x} = e^{-7x}( \cos{2x^{5} + 3x}(10x^{4} + 3) -7\sin{2x^{5} + 3x} )\]

• 자, 여기까지가 직접 식을 전개한 것입니다.
• 매번 미분 문제를 이렇게 해결하기는 어렵습니다. 물론 tensorflow, pytorch 등을 이용하면 자동으로 미분계산을 해줍니다.
• 이번에 다루어 볼 것은 프로그래밍이 아닌 울프람 알파를 이용하여 바로 계산을 해보겠습니다.
• 울프람 알파를 검색해서 사이트를 들어가시거나 Microsoft Store에서 구매해서 사용하셔도 됩니다.

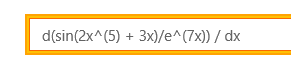
• 먼저 위와같이 검색 창에 derivative 형태로 식을 입력하면 자동으로 계산이 되어집니다. 결과는 다음과 같습니다.

• 앞에서 식을 전개한 것과 동일한 결과가 나옵니다. 심지어 계산 과정까지 잘 정리되어서 나오니… 직접 계산하지말고 이제 식의 의미를 이해하는 데 집중하는것이 좋을 듯 합니다.