Eigen-Things

2018, Sep 27    

Eigenvector, Eigenvalue란 무엇인가?

• 이번 글에서는 선형대수학에서 가장 중요한 내용 중 하나인 eigen의 개념에 대하여 다루어 보려고 합니다.
• eigen이라는 단어는 독일어에서 온 단어이고 뜻은 Characteristic입니다.
• 그러면 characteristic은 어떤 의미를 가지고 있을까요? 먼저 이전 글에서 다루었던 linear transformation을 다시 한번 상기 시켜 보겠습니다.

• 대표적인 transformation은 위의 그림과 같이 scaling, rotation, sheer가 있습니다.
• 위의 transformation을 적용하면 벡터는 다양한 크기와 방향을 가지게 되는데 간단하게 표현하면 평면 형태로 표현할 수 있습니다.

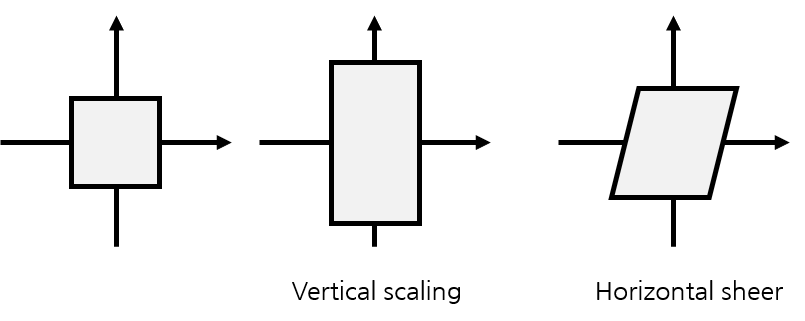
• 위 그림을 보면 벡터들은 다양한 형태로 변형될 수 있고 예를 들어 2번째 그림 처럼 수직으로만 transformation이 될 수 있고 또는 3번째 그림 처럼 수평으로만 transformation이 될 수도 있습니다.
• 하지만 여기서 중요한 것은 과연 모든 벡터들이 다 transformation을 하면 방향성을 다 잃어버릴까 입니다.
• 반대로 얘기하면 transformation이 발생해도 원래 벡터의 방향성 유지하는 벡터들이 있을까 하는 것이 질문의 핵심입니다. 한번 살펴보겠습니다.

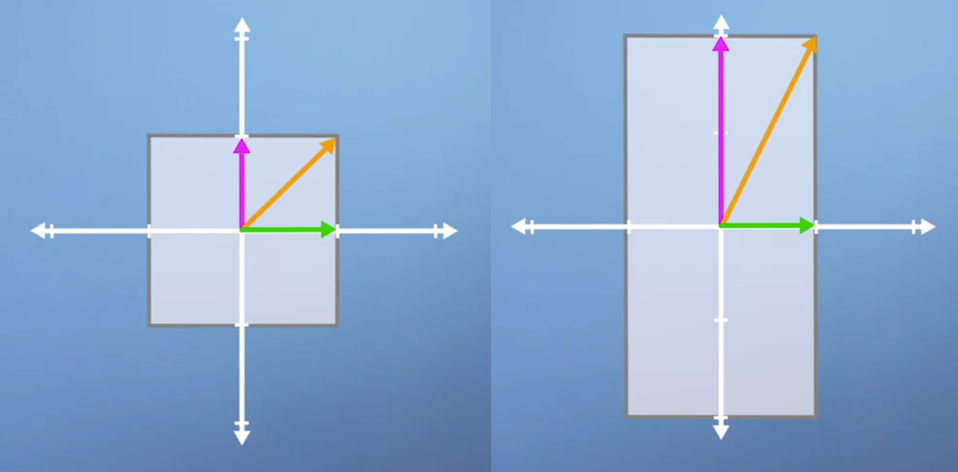
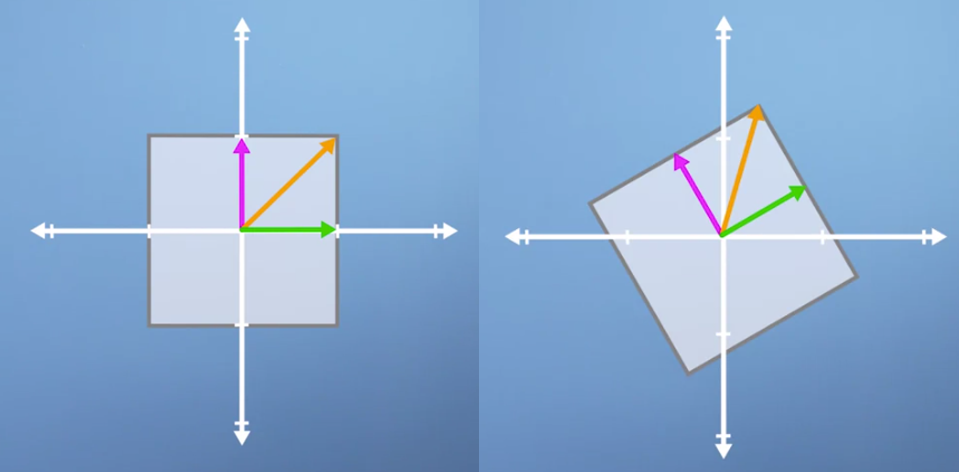
• 위 예제는 수직 방향으로 scaling transformation을 하는 예제 입니다.
• transformation이후에 수평 방향의 초록색 벡터는 전혀 변하지 않았습니다. (방향성도 유지되고 크기도 유지되었습니다.)
• 수직 방향의 보라색 벡터는 방향성은 유지 되었으나 크기는 2배가 되었습니다.
• 마지막으로 대각선 방향의 주황색 벡터는 방향과 크기 모두가 변경되었습니다.
• 위 예제를 보면 수직, 수평방향의 벡터는 위와 같은 transformation이후에도 방향성을 유지하였습니다. 반면 그 사이에 있는 대각선 벡터들은 모두 변경될 것이라는 것을 짐작 하실 수 있을 것입니다.
• 앞에서 언급한 characteristic이 바로 여기서 수직, 수평방향의 벡터입니다. 앞으로 이 벡터를 eigenvector라고 부르겠습니다.
• 이 때, eigenvector와 쌍을 이루는 것이 eigenvalue입니다. 간단히 말하면 eigenvector는 방향성을, eigenvalue는 크기를 나타냅니다.
• 위 예제에서 eigenvector에 해당하는 초록색 벡터는 크기가 변하지 않았습니다. 따라서 eivenvalue는 1입니다. (곱해지는 값이지요)
• 반면에 보라색 벡터의 크기는 2배가 되었습니다. 따라서 eigenvalues는 2입니다.

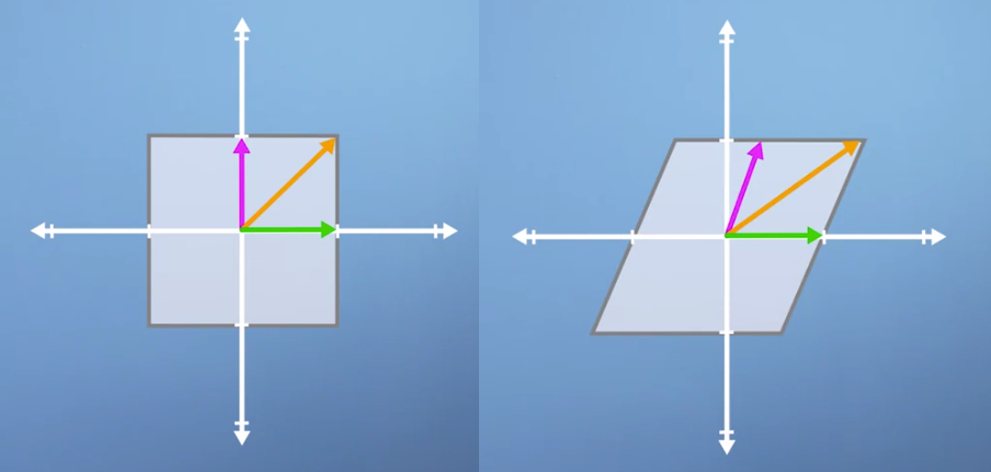
• 위 예제를 보면 eigenvector는 수평의 초록색 벡터 하나 뿐입니다. 왜냐하면 초록색 벡터 하나만 방향성을 유지하였기 때문입니다.

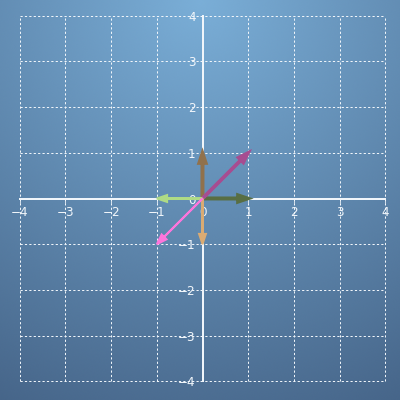
• 위와 같은 경우에는 eigenvector는 없습니다. 벡터의 방향이 모두 변경되었기 때문이지요.

• 위 같은 경우에는 3 벡터 모두 eigenvector입니다. 모두 방향성이 유지되었기 때문입니다. 단 크기가 -가 되었기 때문에 방향이 뒤집어 진 것처럼 보일 뿐입니다.

• 물론 이 개념은 2차원에서만 적용되는 것이 아니라 3,4, …, n차원 모두 적용될 수 있습니다.

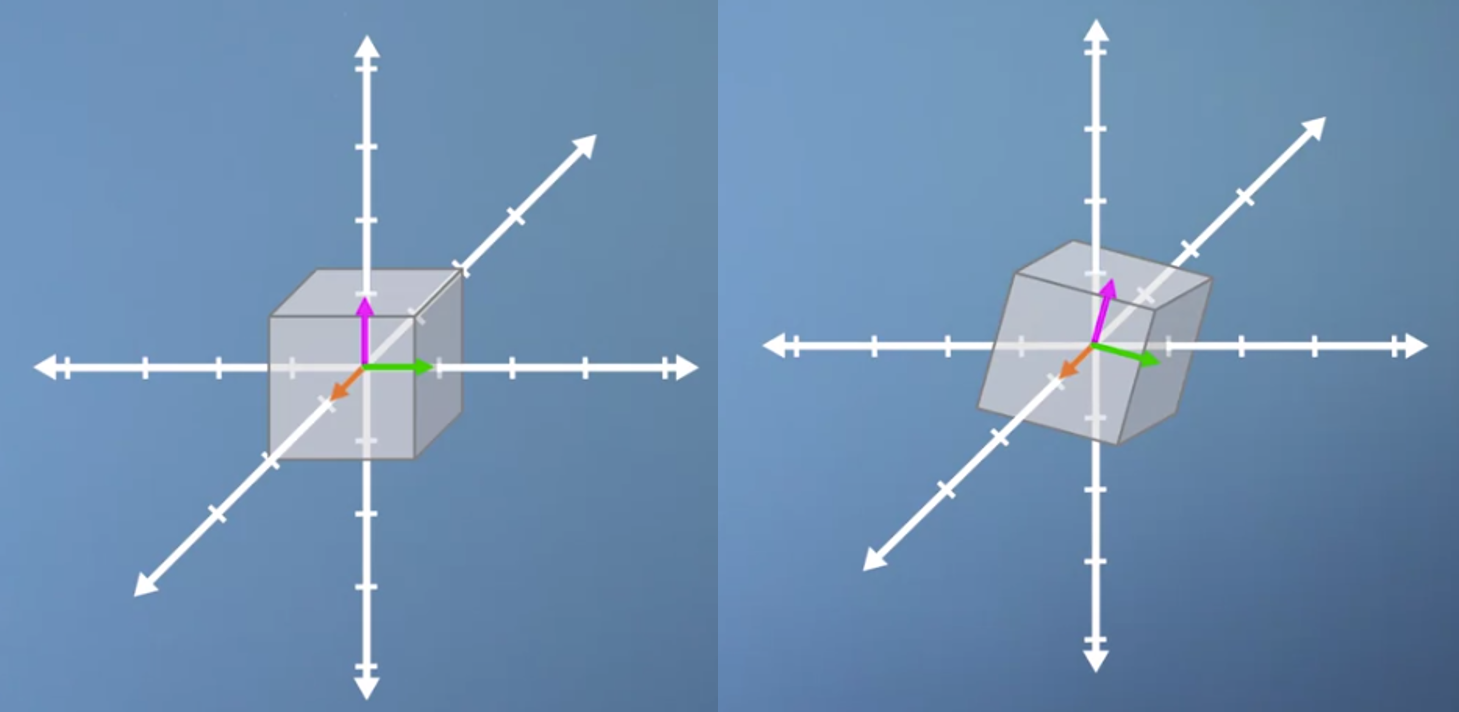
• 위 그림을 보면 주황색 벡터만 오직 eigenvector가 됨을 알 수 있습니다.
• 앞에서 말한 방향성을 조금 더 좋은 표현을 말하면 span이라고 할 수 있습니다.
• 즉, transformation을 거치고 난 이후에도 span이 변경되지 않는 벡터들의 집합을 eigenvector라고 할 수 있겠습니다.
• 이제 eigenvector와 eigenvalue의 정의에 대해서는 알 것 같습니다. 그러면 어떻게 찾아야 할 지 살펴보겠습니다.

Eigenvector, Eigenvalue를 구하는 방법

• 만약 벡터 x가 eigenvector라고 한다면 \(Ax = \lambda x\)의 식으로 표현할 수 있습니다.
• 이 식을 설명을 하면 먼저 \(A\) 는 transformation matrix입니다. 즉, 좌변의 뜻은 eigenvector를 transformation matrix를 통하여 transformation한다는 뜻입니다.
  • 당연히 eigenvector의 정의에 따라 벡터의 방향성은 유지 됩니다.
• 우변의 식은 \(\lambda x\)가 됩니다. 즉 좌변의 transformation matrix에 따라서 벡터의 방향성은 유지되지만 크기는 변경되기 때문에 \(\lambda\)가 곱해집니다.
• 앞에서 정의한 eigenvector의 정의와 똑같은 식입니다!
• 이제 우리의 목적은 양변을 같게 만들어 줄 수 있는 eigenvector \(x\)를 찾는 것입니다.
• transformation matrix \(A\)의 dimension은 (n, n)입니다. 좌변과 우변이 같도록 크기를 맞춰주기 위해서도 (n, n) 크기의 행렬이 되어야 하는 것도 맞지만 정확한 뜻은 \(A\)가 n-dimensional transformation이므로 (n,n)크기이어야 한다고 해석할 수 있습니다.

• 자, 그러면 방정식을 풀기 위하여 좌변으로 옮겨 보면 \((A - \lambda I)x = 0\)이 됩니다.
• 이 때, \((A - \lambda I) = 0\) 또는 \(x = 0\)이 되면 됩니다. 하지만 이때, \(x = 0\)이 되는 것은 전혀 의미가 없으므로 무시합니다.
• 그러면 \((A - \lambda I) = 0\)이 되는 해를 찾아야 합니다. 해 \(\lambda\)를 구하기 위하여 양변에 determinant를 취해줍니다.
  • 즉, \(det(A - \lambda I) = 0\)이 됩니다.
• 만약 \(A = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}\) 라면 \(det( \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} - \begin{pmatrix} \lambda & 0 \\ 0 & \lambda \\ \end{pmatrix} ) = 0\)이 됩니다.
  • 정리하면 \(\lambda^{2} -(a + d)\lambda + (ad - bc) = 0\)가 됩니다.

• 앞에서 예를 든 수직 방향으로 2배 늘린 예제로 한번 계산해 보겠습니다.
• 위 transform에서 transformation matrix는 \(A = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}\) 형태가 됩니다.

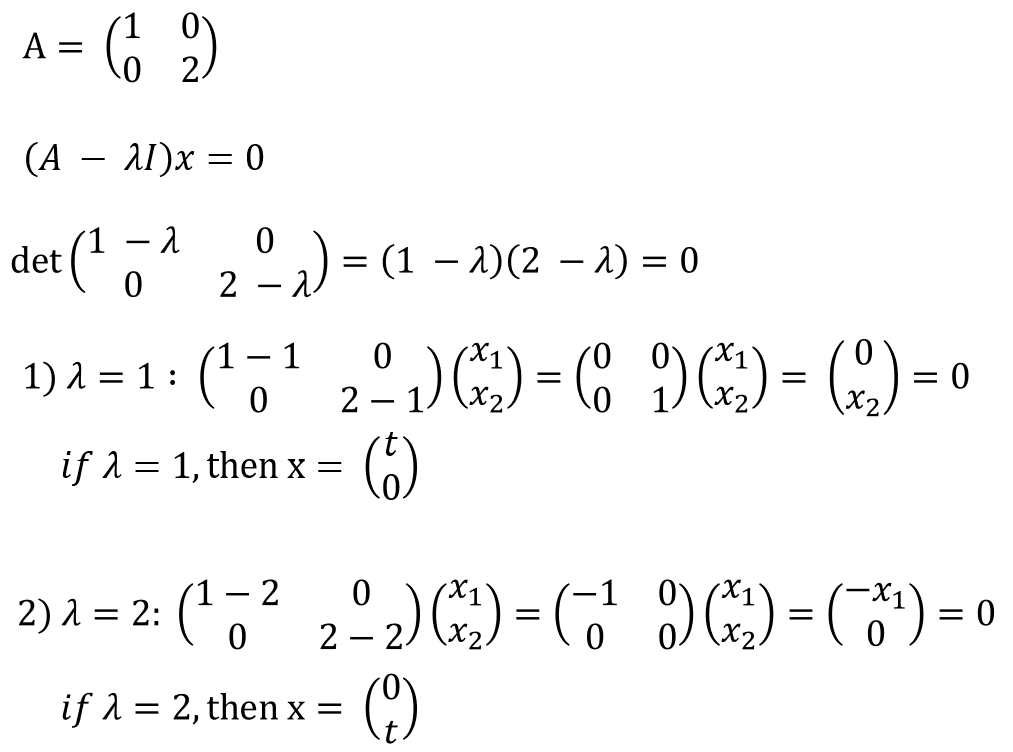
• 위 식을 보면 먼저 방정식을 통하여 \(\lambda\) 값 2개를 구하였습니다.
• 먼저 \(\lambda = 1\)일 때 마지막 결과를 보면 \(x_{2}\)는 반드시 0이되어야 하고 \(x_{1}\)에 대한 제약은 없으므로 임의의 값이 들어갈 수 있습니다.
  • 따라서 \(\begin{pmatrix} t \\ 0 \\ \end{pmatrix}\)로 표현할 수 있습니다.
• 반면 \(\lambda = 1\)일 때를 보면 \(x_{1}\)는 반드시 0이되어야 하고 \(x_{2}\)에 대한 제약은 없으므로 임의의 값이 들어갈 수 있습니다.
  • 따라서 \(\begin{pmatrix} 0 \\ t \\ \end{pmatrix}\)로 표현할 수 있습니다.
• 이 결과를 보면 수직 방향으로 linear transformation을 하면 수직 축 상의 벡터와 수평 선 상의 벡터의 크기는 달라지지만 방향은 달라지지 않아서 eigenvector가 된다는 내용가 정확히 일치합니다.

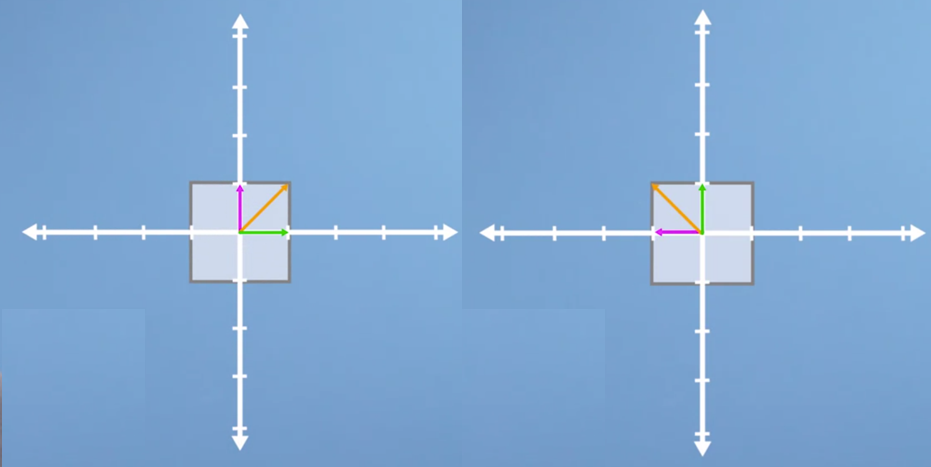
• 만약 위와 같이 90도 반시계방향으로 회전하면 어떻게 될까요? 일단 기하학적으로 보면 eigenvector는 존재하지 않습니다. 실제 계산도 그렇게 나오는지 살펴보겠습니다.
• 반시계 방향으로 90도 회전하는 transformation matrix는 \(A = \begin{pmatrix} 0 & -1 \\ 1 & 0 \\ \end{pmatrix}\) 이므로 \(det \begin{pmatrix} -\lambda & -1 \\ 1 & -\lambda \\ \end{pmatrix} = \lambda^{2} + 1 = 0\) 이 됩니다.
• 위 방정식을 풀면 \(\lambda\)에 해당하는 실수 해가 없으므로 eigenvector는 존재하지 않습니다.

Eigenbasis에 관하여

• eigenvector의 개념과 이전 글에서 다루었던 changing basis의 개념을 결합하여 계산을 효율적으로 하는 방법에 대하여 한번 다루어 보겠습니다.
• 이전에 diagonalisation에 대하여 먼저 알아보겠습니다.
• 때때로, 우리는 같은 행렬을 여러번 곱해야 할 일이 있습니다. 만약 성분이 대각선에만 존재하고 나머지 성분은 0인경우인 대각행렬을 여러번 곱하면 어떻게 될까요?
• 이 경우에 행렬연산은 상당히 간단합니다. \(T = \begin{pmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \\ \end{pmatrix}\) 이면 \(T^{n} = \begin{pmatrix} a^{n} & 0 & 0 \\ 0 & b^{n} & 0 \\ 0 & 0 & c^{n} \\ \end{pmatrix}\)가 됩니다.
• 대각 행렬의 경우 위와 같이 간단하게 연산이 되지만 대각 행렬이 아닌 경우의 n제곱 연산은 어떻게 해야 할까요? 정답은 대각 행렬이 아닌 행렬을 대각 행렬로 바꾸는 것에 있습니다.
• 즉, n제곱을 해야 할 행렬을 대각행렬과 대각행렬이 아닌 행렬의 곱으로 나타내는 방법인데, 이 방법을 eigenbasis라고 합니다.
• eigenbasis를 구현하기 위하여 eigenbasis conversion matrix를 만들어 보겠습니다. 먼저, eigenvector를 열벡터로 구성합니다.
  • 즉, \(C = (x_{1}, x_{2}, x_{3})\)가 됩니다. 이 때, \(x_{1}, x_{2}, x_{3}\)는 열벡터 이며 eigenvector입니다.
• 다음으로 행렬 \(D\)는 대각 행렬이고 그 대각 성분은 행렬 \(C\)의 eigenvector에 대응하는 eigenvalue로 구성되어 있습니다.
  • 즉, \(C = \begin{pmatrix} \lambda_{1} & 0 & \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{pmatrix}\)가 됩니다.
• 만약 어떤 행렬 \(T\)를 대각 행렬 성분으로 바꾸고 싶다면 \(T = CDC^{-1}\)로 바꿀 수 있습니다.
• 이 행렬의 경우 제곱을 하면 \(T^{2} = CDC^{-1}CDC^{-1} = CD^{2}C^{-1}\)이 됩니다. 일반화 시키면 \(T^{n} = CD^{n}C^{-1}\)이 됩니다.

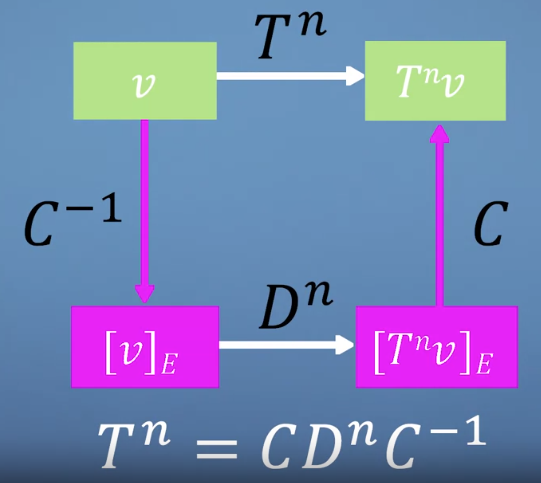
• 위 과정을 보면 transformation matrix를 쓰는 과정과 똑같습니다. 이런 방법을 이용하면 직접적으로 n제곱하는 연산보다 훨씬 효율적으로 계산할 수 있습니다.

• 예를 들면 위와 같이 단순이 행렬을 제곱하는 것과 eigenbasis를 이용하는 것의 결과가 같음을 알 수 있습니다.