multivariate calculus와 jacobian

2019, Sep 28    

mathematics for machine learning 글 목록

• 이 글은 Coursera의 Mathematics for Machine Learning: Multivariate Calculus 을 보고 정리한 내용입니다.

목차

• variables, constants & context

• differentiate with respect to anything

• jacobian

• jacobian applied

• Sandpit

• Hessian

• Reality is hard

variables, constants & context

• 앞의 글인 basic alculus에서는 어떤 점에서 함수의 미분을 하는 방법에 대하여 다루어 보았습니다.
• 특히 이전 글에서 다룬 케이스들은 variable이 1개인 single variable의 경우에 한정해서 보았었습니다.
• 이번 글에서 다루어 볼 것은 variable의 갯수가 여러개인 multivariate system에 대하여 다루어 보려고 합니다.
• multivariate에 대하여 다루어 보기전에 variable이 하는 역할에 대하여 먼저 확인을 해보도록 하겠습니다.

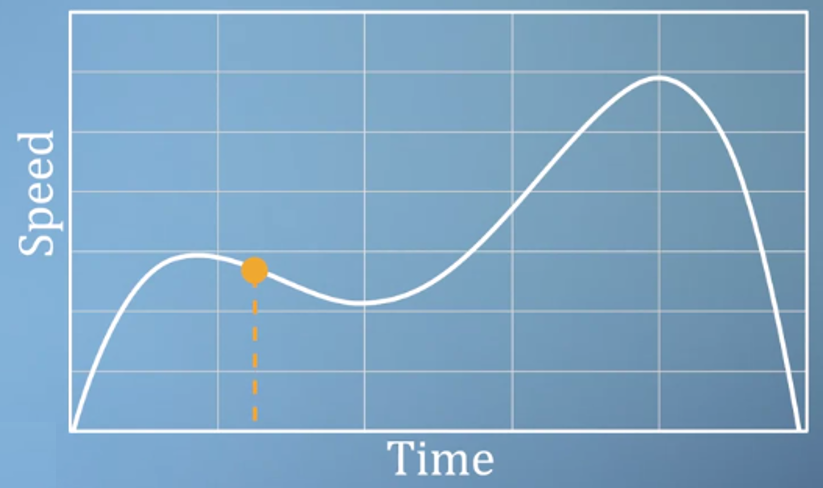
• 예를 들어 위 그래프는 자동차의 특정 시간에 따른 속력 데이터입니다. 특정 시간에 자동차가 가질 수 있는 속력은 1개이므로 위 그래프는 명확합니다.
• 즉, 위 그래프에서 time이 independent variable이 됩니다. speed는 time에 따른 함수 값이 되는 것입니다.

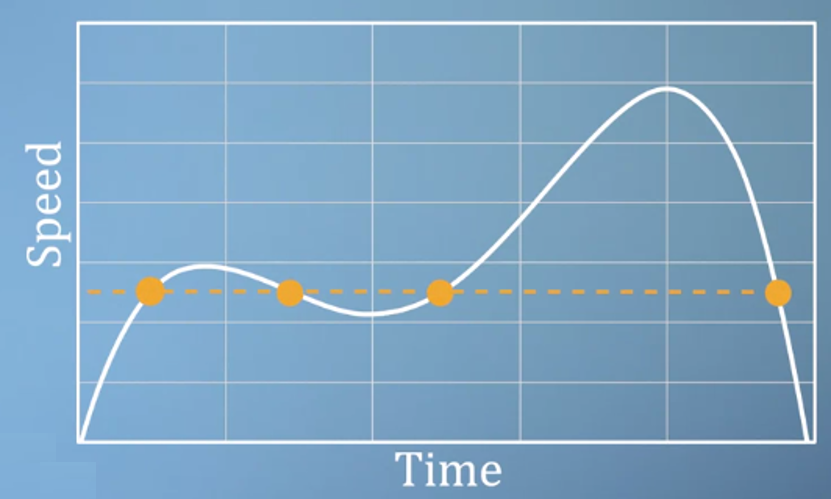
• 그러나 반대로 위와 같이 speed를 independent variable로 가져갈 수는 없습니다. 왜냐하면 함수의 정의 상 한 개의 입력 값에 대하여 한 개의 함수값이 대응 되어야 하기 때문에 함수의 정의에 맞지 않게 됩니다.
• 이러한 이유로 speed는 dependent variable이 되어야 합니다.
• 즉, 어떤 변수를 independent 또는 dependent variable로 정할 지는 그 상황에 맞추어서 정해야 합니다.

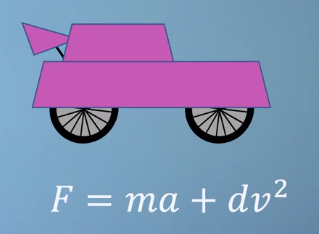
• 예를 들어 위 그림과 같은 차가 있고 이 차의 엔진이 만들어내는 힘 \(F\)는 위 식을 따른다고 가정해 보겠습니다.
• 위 식에서 \(m\) 은 mass, \(a\)는 acceleration, \(d\)는 drag coefficient, \(v\)는 velocity라고 하겠습니다.
• 만약 내가 운전자 입장에서 variable들을 관찰해 본다면 \(m\)과 \(d\)는 고정된 상수 값입니다. 왜냐하면 운전중에 이 값은 변경할 수 없는 값이기 때문입니다.
• 운전자 입장에서 자연스러운 위 식의 해석을 하려면 \(F\)가 independent variable이고 \(a\)와 \(v\)가 dependent variable이어야 합니다. 왜냐하면 엔진이 내는 힘에 따라서 속도와 가속도가 어떻게 변하는 지를 접근하는 것이 적합하기 때문입니다.
• 이렇게 해석하면 \(m, d\)는 constant이고 \(a, v\)는 dependent variable이고 \(F\)는 independent variable이 됩니다.

• 반면에 자동차 설계를 하는 입장에서는 특정 velocity와 acceleration이 정해져 있고 mass와 drag coefficient가 변화할 때, 엔진의 힘이 어떻게 변화하는 지 관찰해야 할 수 있습니다.
• 이 경우에는 \(a, v\)가 constant이고 \(m, d\)가 independent variable이고 \(F\)가 dependent variable이 됩니다.
• 즉, 요점은 상황에 따라 어떤 값이 constant, independent/dependent variable이 될 수 있기 때문에 그 문맥을 잘 파악하는 것이 중요하다는 점입니다.

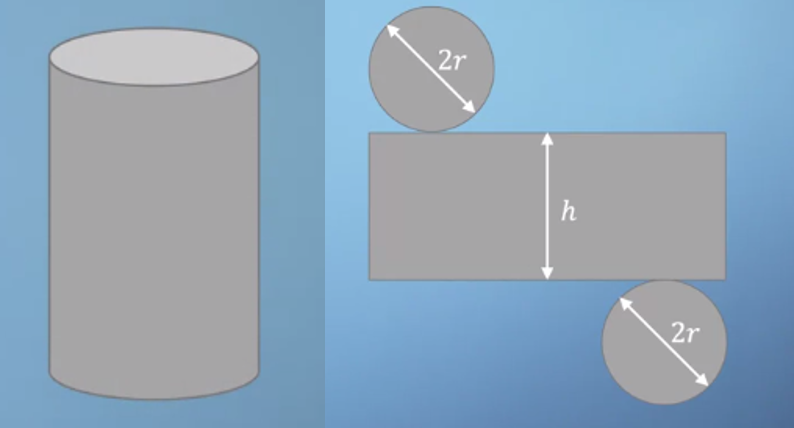
• 이번에는 다른 예제를 한번 살펴보겠습니다. 위 그림과 같이 생긴 캔이 있고 이 캔의 전개도를 펼쳐보았습니다. 옆면에 해당하는 사각형의 세로 길이는 \(h\) 이고 가로 길이는 밑면인 원의 둘레인 \(2\pi r\)이 됩니다.
• 이 캔이 가지는 mass를 한번 구해보면 다음과 같습니다. 여기서 사용된 \(t\) 는 thickness이고 \(\rho\)는 density 입니다.

• \[m = 2\pi r^{2} t \rho + 2\pi r h t \rho\]

• 이 식에서는 \(\pi\) 빼고는 모든 값이 variable이 될 수 있습니다. radius, height, tickness, density 모두가 변화할 수 있는 값입니다.
• 그러면 변화할 수 있는 값에 대하여 미분을 해보겠습니다. 즉, \(r, h, t, \rho\)에 대하여 각각의 미분을 하려고 합니다.
• 여기서 중요한 것은 어떤 variable에 대하여 미분을 하면 나머지 변수들은 상수 취급을 할 수 있다는 것입니다.
• 미분 즉, derivative의 정의가 특정 값의 변화에 따른 함수 값의 변화 (rise over run) 이기 때문에 미분해야 할 특정 값이 정해지면 나머지 변수들은 상수 취급을 하는 것이 정의에 맞습니다.
• 그러면 각 변수에 대하여 미분을 해보도록 하겠습니다.

• \[m = 2\pi r^{2} t \rho + 2\pi r h t \rho\]
• \[\frac{\partial m}{\partial h} = 2\pi r t \rho\]
• \[\frac{\partial m}{\partial r} = 4\pi r t \rho + 2\pi t \rho\]
• \[\frac{\partial m}{\partial t} = 2\pi r^{2} \rho + 2\pi r h \rho\]
• \[\frac{\partial m}{\partial \rho} = 2\pi r^{2} t + 2\pi r h t\]

• 위 수식 기호에서 볼 수 있는 것 처럼 multivariate 상황에서 미분을 할 때에는 \(\text{d}\) 대신 \(\partial\)을 씁니다.
• 수식의 결과를 보면 미분하려는 변수가 없는 항이 소거되는 것을 볼 수 있는데 이것은 특정 상수를 미분하면 소거하는 것과 똑같은 이유입니다.
• 위 수식과 같은 전개를 partial derevative 이라고 합니다. partial derevative을 이용하면 multi dimensional problem을 다룰 수 있습니다. 여러개의 변수를 동시에 생각하지 않고 변수들을 분리해서 생각하기 때문에 1d differentiation 문제를 해결하는 것 처럼 접근할 수 있는 것입니다.

differentiate with respect to anything

• 앞에서 배운 partial derevative를 조금 더 복잡한 수식에 대입하여 한번 살펴보도록 하겠습니다.

• \[f(x, y, z) = \sin{(x)} e^{yz^{2}}\]

• 그러면 \(x, y, z\) 각각에 대하여 미분을 해보도록 하겠습니다.

• \[\frac{\partial f}{\partial x} = \cos{(x)} e^{yz^{2}}\]
• \[\frac{\partial f}{\partial y} = \sin{(x)} e^{yz^{2}} z^{2}\]
• \[\frac{\partial f}{\partial z} = \sin{(x)} e^{yz^{2}} 2yz\]

• 그러면 각각의 partial derivative 결과를 이용하여 좀 더 응용된 문제를 풀어보겠습니다.
• 만약 \(x, y, z\)가 변수 \(t\)를 치환한 형태라고 생각해 보겠습니다.

• \[x = t - 1\]
• \[y = t^{2}\]
• \[z = \frac{1}{t}\]

• 이 식의 경우 좀 간단하기 때문에 실질적으로는 다음과 같이 간단하게 정리 됩니다.

• \[f(t) = \sin{(t - 1)}e^{t^{2}(\frac{1}{t})^{2}} = \sin{(t - 1)}e\]
• \[\frac{\text{d}f(t)}{\text{d}t} = \cos{(t-1)}e\]

• 하지만 이와 같은 경우는 사실 상당히 운이 좋아서 간단하게 정리되었습니다.
• 많은 경우 직접 대입하였을 때, 더 복잡해 지는 경우가 많기 때문에 이번에는 치환한 형태를 이용해 보도록 하겠습니다.
• 앞에서 다룬 partial derivative를 살펴보면 multivariate 케이스를 단일 변수를 이용하여 접근하는 방법을 사용하였습니다.
• 이번에 다룰 total derivative는 partial derivative의 합은 원 함수의 derivative가 된다는 성질을 이용하는 방법입니다.
• 즉 앞에서 \(\text{d}f(t) / \text{d}t\) 의 결과와 각각의 partial derivative인 \(\text{d}f(x, y, z) / \partial x\), \(\text{d}f(x, y, z) / \partial y\), \(\text{d}f(x, y, z) / \partial z\)를 모두 합친 것에 \(x = t-1, y = t^{2}, z = 1/t\)를 대입한 것의 결과가 같다는 것입니다.
• 정리하면 변수 \(t\)로 이루어진 어떤 식을 치환한 값인\(x, y, z\)로 이루어진 식 \(f(x, y, z)\)를 \(t\)로 정리한 다음 \(t\)에 대하여 미분한 식을 ①이라 하고
• 그 다음으로 \(f(x, y, z)\)를 각각의 \(x, y, z\)에 대하여 partial derivative를 구한 뒤 모두 더한 값에 \(t\)로 이루어진 치환식을 대입하면 결과가 같다는 것이 total derivative입니다.
• 즉, ① 대입 → 미분을 할 것인지 ② 편미분 → 대입할 것인에 대한 순서의 차이입니다.
• 하지만 ②의 경우 치환을 한 상태이기 떄문에 식이 간단해져 있고 편미분의 특성상 미분의 결과가 간단해 지기 때문에 ②를 이용하면 식을 좀 더 간단하게 전개할 수 있는 경우가 많습니다.
• 앞의 예제를 total derivative 방법을 통해 풀어보겠습니다.

• \[\frac{\text{d}f(x, y, z)}{\text{d}t} = \frac{\partial f}{\partial x}\frac{\text{d}x}{\text{d}t} + \frac{\partial f}{\partial y}\frac{\text{d}y}{\text{d}t} + \frac{\partial f}{\partial z}\frac{\text{d}z}{\text{d}t}\]
• \[x = t - 1 \quad y = t^{2} \quad z = \frac{1}{t}\]
• \[\frac{\partial f}{\partial x} = \cos{(x)}e^{yz^{2}} \quad \frac{\text{d}x}{\text{d}t} = 1\]
• \[\frac{\partial f}{\partial y} = z^{2}\sin{(x)}e^{yz^{2}} \quad \frac{\text{d}y}{\text{d}t} = 2t\]
• \[\frac{\partial f}{\partial z} = 2yz \sin{(x)}e^{yz^{2}} \quad \frac{\text{d}z}{\text{d}t} = -t^{-2}\]
• \[\frac{\text{d}f(x, y, z)}{\text{d}t} = \frac{\partial f}{\partial x}\frac{\text{d}x}{\text{d}t} + \frac{\partial f}{\partial y}\frac{\text{d}y}{\text{d}t} + \frac{\partial f}{\partial z}\frac{\text{d}z}{\text{d}t} = \cos{(x)}e^{yz^{2}} \times 1 + z^{2}\sin{(x)}e^{yz^{2}} \times 2t + 2yz \sin{(x)}e^{yz^{2}} \times -t^{-2}\]
• 여기 까지 정리한 것이 total derivative 입니다.
• 그러면 여기서 치환 값인 \(x, y, z\)에 \(t\)를 이용한 식들을 대입해 보겠습니다.

• \[x = t - 1\]
• \[y = t^{2}\]
• \[z = \frac{1}{t}\]

• \[\frac{\text{d}f(x, y, z)}{\text{d}t} = \cos{(t-1)}e + t^{-2}\sin{(t-1)}e \times 2t + 2t\sin{(t-1)}e \times (-t^{-2}) = \cos{(t-1)}e\]

• 따라서 ① 과 ②의 결과가 같음을 알 수 있습니다.

• 지금까지 살펴본 내용이 이해가 잘 되었다면 아래 예제를 한번 풀어보시길 권장 드립니다.
• 예제를 푸시면서 total derivative를 사용하면 문제를 쉽게 해결할 수 있다는 것을 느끼시면 됩니다.

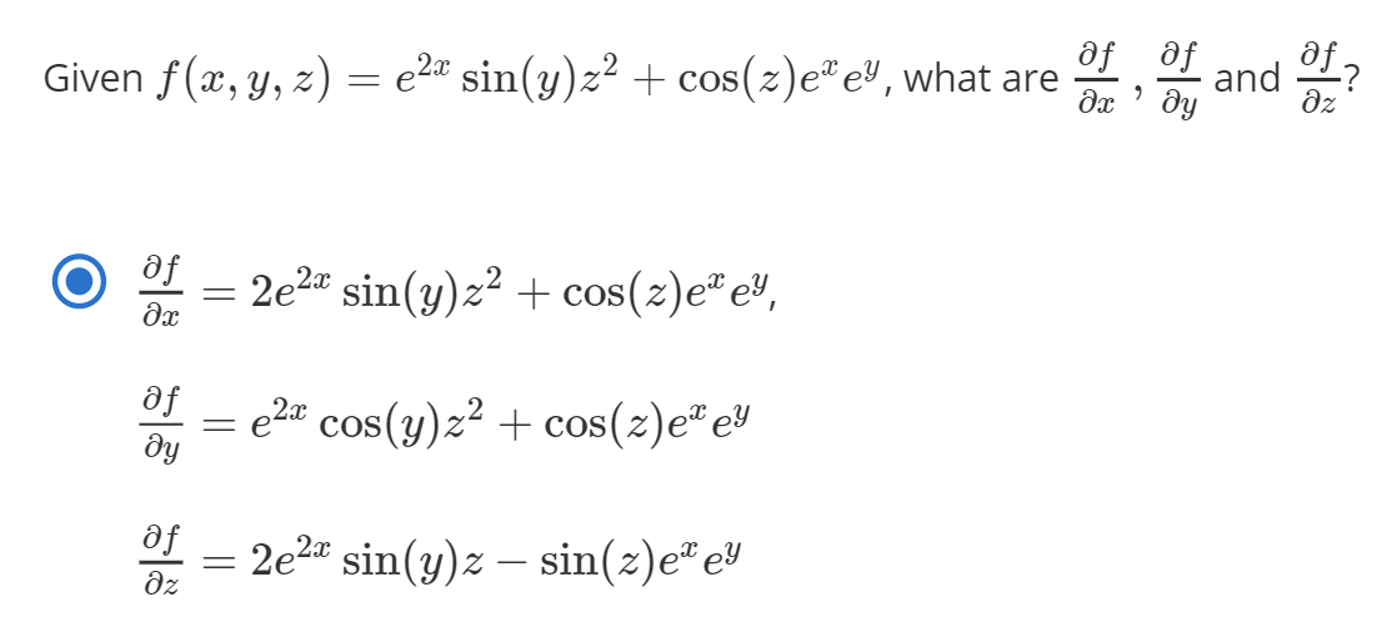
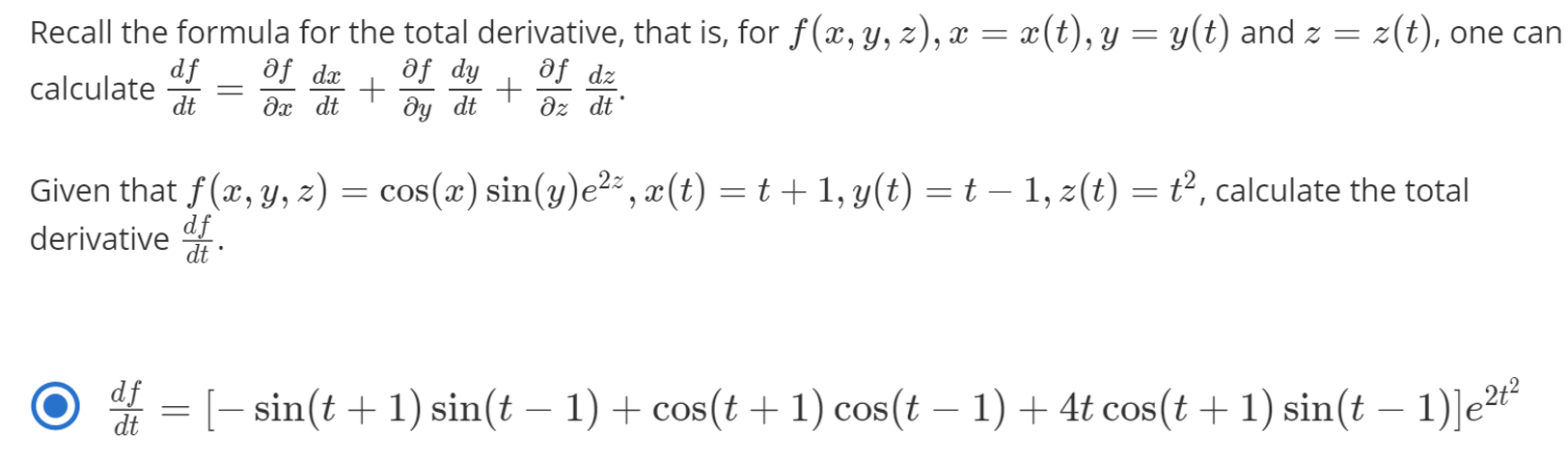
jacobian

• 앞에서 배운 partial derivative를 좀 더 간편하게 표현하기 위하여 선형 대수학의 개념을 조금 끌어와서 jacobian 벡터란 것에 대하여 알아보도록 하겠습니다.
• jacobian 벡터는 multivariate를 가지는 어떤 function에 각각의 variable에 관하여 미분을 하였을 때의 결과를 행벡터 형식으로 나타낸 것입니다.

• \[f(x_{1}, x_{2}, ...)\]
• \[J = \begin{bmatrix} \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}} & \frac{\partial f}{\partial x_{3}} & ...\end{bmatrix}\]

• 예를 들어 다음 식을 자코비안 벡터 J로 나타내 보겠습니다.

• \[f(x, y, z) = x^{2}y + z\]
• \[\frac{\partial f}{\partial x} = 2xy\]
• \[\frac{\partial f}{\partial y} = x^{2}\]
• \[\frac{\partial f}{\partial z} = 3\]
• \[\therefore \quad J = (2xy, x^{2}, 3)\]

• 위에서 구한 J에 대하여 다시 생각해 보면 각 열은 \(x, y, z\)에 대하여 편미분을 한 것이므로 각 축의 변화량에 의한 함수값의 변화량이라고 생각하시면 됩니다.

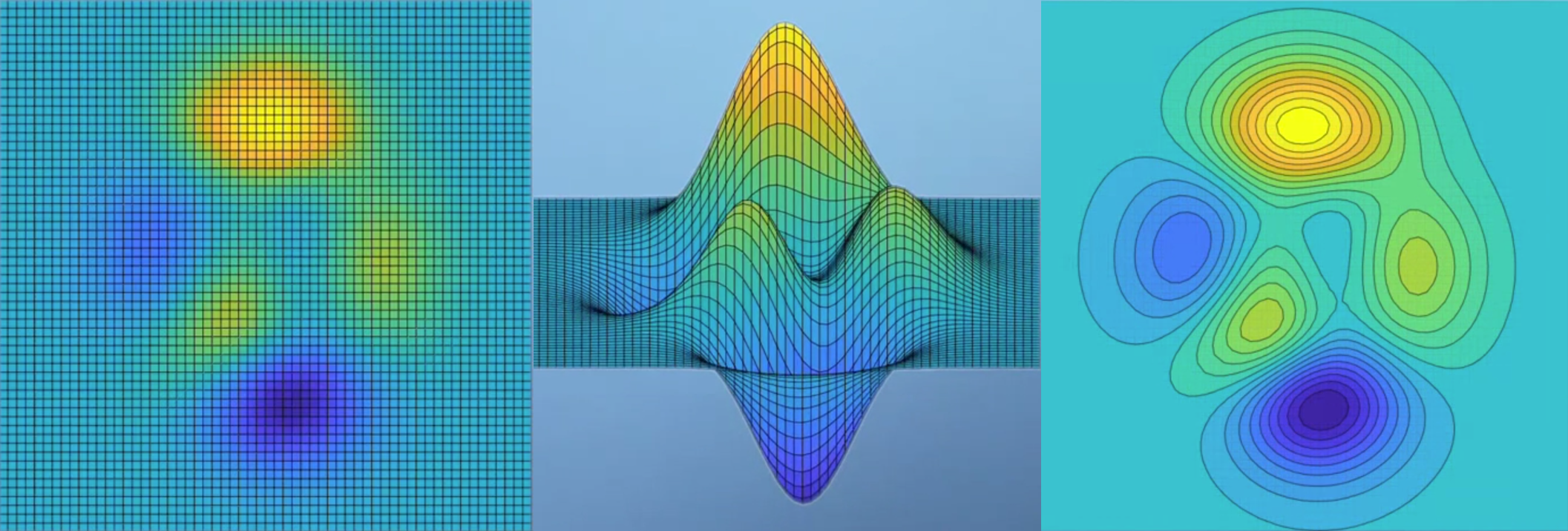
• 위 그림과 같이 3차원 데이터를 색(밝은 노란색 : z값이 큼, 짙은 파란색 : z값이 작음)과 등고선 형태로 나타낸 그래프가 있다고 생각해 보겠습니다.
• 그러면 지금부터 각 지점에서 자코비안 벡터를 적용하였을 때, 그 값의 의미에 대하여 알아보겠습니다.

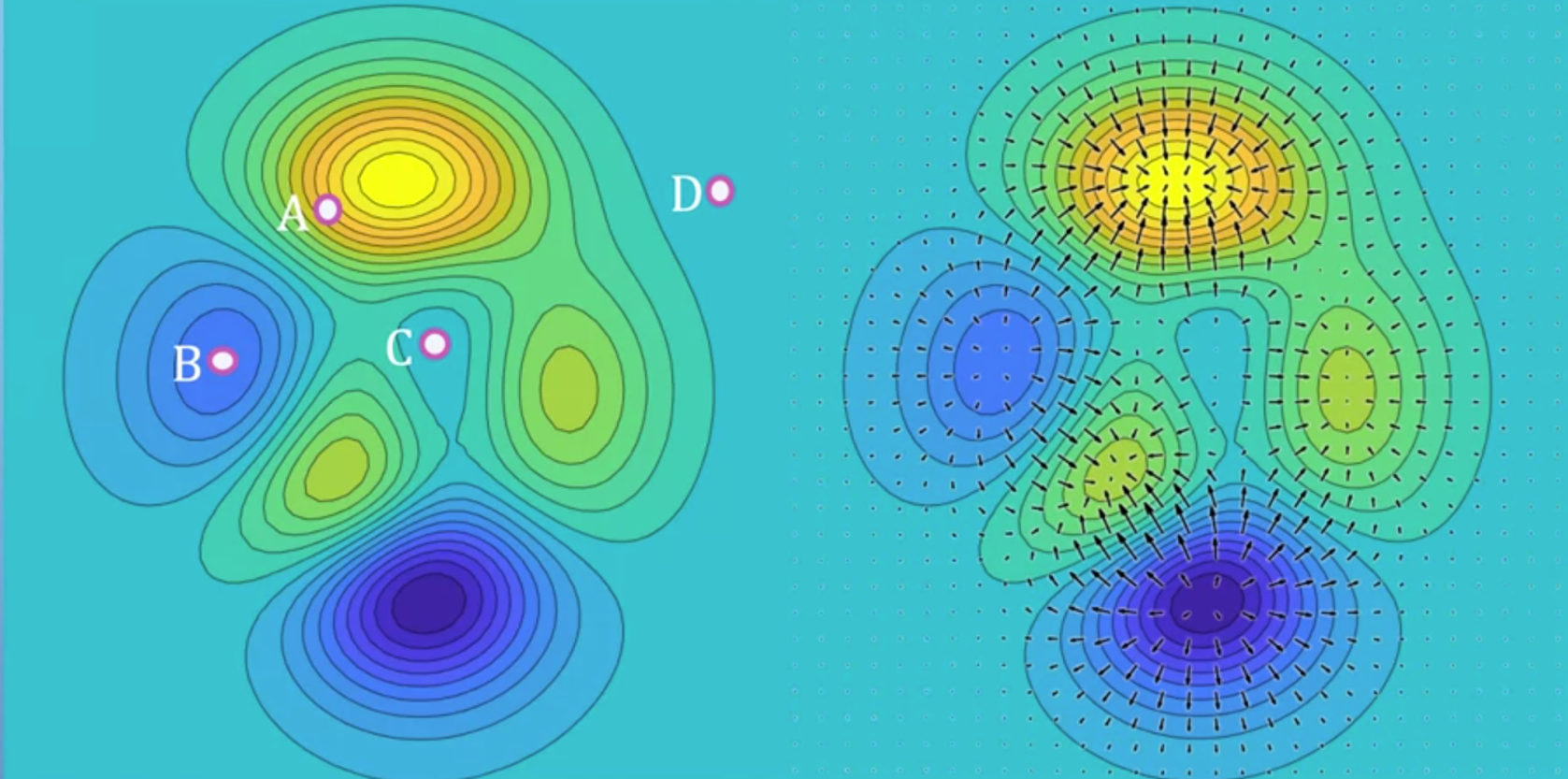
• 여기서 자코비안은 미분 즉, 변화량을 가지고 있는 벡터 입니다. 변화량을 2차원 그래프 또는 3차원 그래프에서 나타내면 그래프에서의 경사로 나타낼 수 있고 위 그래프가 하나의 예시가 될 수 있습니다.
• 등고선으로 나타내었을 때, 등고선이 빽빽할수록 경사가 가파른 것이고 변화량이 크다고 말할 수 있습니다.
• 위 그래프와 같은 값을 가지는 함수에서 자코비안 벡터를 구하면 각 지점에서의 함수의 변화량을 얻을 수 있습니다.
  • 말 그대로 벡터이기 때문에 크기와 방향을 모두 가지고 있습니다.
  • 위 그래프에서 화살표의 길이가 길고 선명하면 변화량이 큰 것입니다.
  • 따라서 특정 지점의 변화량을 나타내려면 그 특정 지점을 시작점으로 하고 자코비안 벡터값을 크기와 방향으로 나타내면 위 그림과 같은 vector field를 나타낼 수 있습니다.
• 따라서 4개의 점 A, B, C, D 중에서 A지점의 변화량이 가장 크므로 자코비안 벡터의 값 또한 가장 큽니다.
• 반면 가장 밝은 곳 또는 가장 어두운 곳은 flat 하므로(변화량이 작으므로) 자코비안의 값은 작아지게 됩니다.

jacobian applied

• 앞에서 배운 jacobian 개념을 벡터에서 행렬로 확장시켜 보겠습니다. jacobian을 행렬로 확장시키면 함수값이 벡터 형태를 가지는 경우를 다룰 수 있습니다.
• 먼저 간단한 식을 이용하여 jacobian 벡터를 구해보도록 하겠습니다.

• \[f(x, y) = e^{-(x^{2} + y^{2})}\]
• \[J = \begin{bmatrix} -2xe^{-(x^{2} + y^{2})}, & -2ye^{-(x^{2} + y^{2})} \end{bmatrix}\]

• jacobian 벡터는 말 그대로 벡터이기 때문에 값과 크기를 가집니다. 몇 가지 예제를 구해보겠습니다.

• \[J(-1, 1) = \begin{bmatrix} -2xe^{-2}, & -2ye^{-2} \end{bmatrix} = \begin{bmatrix} 0.27, & -0.27 \end{bmatrix}\]
• \[J(2, 2) = \begin{bmatrix} -0.001, & -0.001 \end{bmatrix}\]
• \[J(0, 0) = \begin{bmatrix} 0, & 0 \end{bmatrix}\]

• 앞에서 구한 3가지 jacobian 벡터를 각 시작점에서 벡터로 나타내면 왼쪽 그림과 같습니다.
• 이것을 전체 값에 확장해서 vector field로 나타내면 오른쪽 그림처럼 나타낼 수 있습니다.
• 특히 노란색 지점과 같이 minimum 값을 가지는 경우를 saddle 이라고도 합니다.
• 여기까지는 앞에서 배운 내용과 같습니다. 이제 확장해 보도록 하겠습니다.

• 다음과 같은 두 공간이 있다고 가정해 보겠습니다. 한 공간은 \(x, y\)로 이루어져 있고 다른 공간은 \(u, v\)로 이루어져 있습니다. 특히 \(u, v\)는 아래와 같이 \(x, y\)로 이루어져 있습니다.

• \[u(x, y) = x - 2y\]
• \[v(x, y) = 3y - 2x\]

• 앞의 예제에서는 함수 식이 하나 밖에 없었기 때문에 jacobian을 벡터 형태로 나타내었습니다.
• 하지만 이번 경우에는 함수 식이 2개로 늘었습니다. 따라서 jacobian의 행벡터를 누적해서 아래로 쌓아서 행렬 형태로 만들면 이 문제를 해결할 수 있습니다. 이러한 이유로 보통 사용하는 열벡터 대신 행벡터를 앞에서 사용하였습니다.

• \[u(x, y) = x - 2y\]
• \[v(x, y) = 3y - 2x\]
• \[J_{u} = \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \end{bmatrix}\]
• \[J_{v} = \begin{bmatrix} \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{bmatrix}\]
• \[J = \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{bmatrix} = \begin{bmatrix} 1 & -2 \\ -2 & 3 \end{bmatrix}\]

• 특히 위 행렬은 결과적으로 \(x, y\)공간을 \(u, v\) 공간으로 단순히 linear transformation 한 형태를 가지게 됩니다. (x, y의 계수와 jacobian 행렬의 값을 비교해 보면 \(x - 2y\)의 계수가 1행의 값이고 \(-2x + 3y\)가 2행의 값입니다.)
• 이것은 당연한 것인데 왜냐하면 \(u, v\)가 선형식(1차식)이기 때문입니다. 즉, 변화량이 상수값이기 때문에 항상 그 상수 값 만큼만 변환된 것입니다.
• jacobian의 묘미는 1차 (편)미분을 이용하여 공간1 → 공간2로 linear transformation하는 것입니다.
• 1차 미분을 하는 것이 곡선에 접한 접선의 식을 구하는 것이고 non-linear/linear 한 공간을 linear 한 공간으로 approximation한다고 이해하면 됩니다.

• 그러면 jacobian을 사용하는 유명한 예제인 직교 좌표계를 극 좌표계로 변환하는 예제를 한번 다루어 보겠습니다.
  • 링크의 가우스 적분 내용을 살펴 보시면 이해가 잘 되실 수 있습니다.

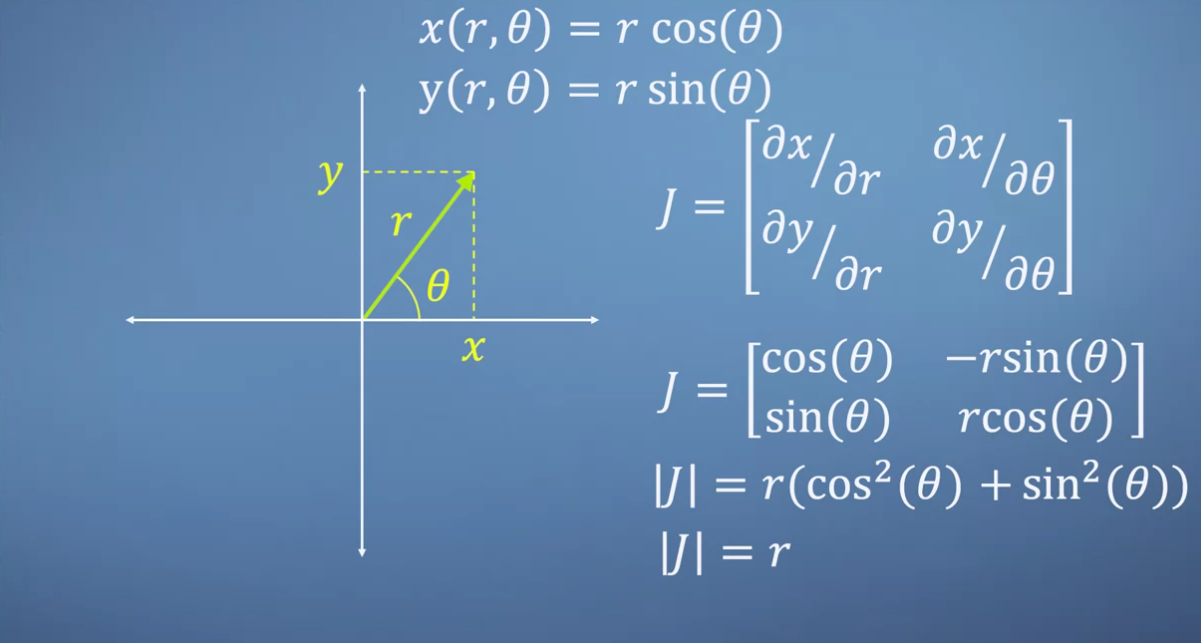
• 이 글에서는 변환의 자세한 의미 보다 jacobian 관점에서 설명을 해보겠습니다. 먼저 \(x, y\)와 \(r, \theta\)의 관계식은 삼각 함수를 통해 정의할 수 있습니다. 여기서 \(x, y\)를 통해 나타내는 좌표계가 직교 좌표계이고 \(r, \theta\)로 나타내는 좌표계가 극 좌표계 입니다.
• 직교 좌표계와 극 좌표계는 서로 사용하는 space가 다르기 때문에 서로 다른 변화량을 가지게 됩니다.
• 직교 좌표계에서의 각 축의 변화 \(\Delta x, \Delta y\)에 의해 변화량은 \(\Delta x \cdot \Delta y\)만큼의 값을 가지게 됩니다. 직사각형의 면적 처럼 나타낼 수 있습니다.
• 직교 좌표계의 변화를 극 좌표계의 변화와 연관 시켜 보려면 jacobian을 통하여 linear transformation 하여 두 space의 관계를 보면 됩니다. 그러면 위 슬라이드 처럼 jacobian matrix \(J\)를 구할 수 있습니다.
• 이 때, \(J\)의 determinant를 계산하면 determinant의 정의에 따라 변화량의 scale을 계산할 수 있습니다. 슬라이드의 계산에 따라 변화량의 scale은 \(r\) 입니다.

• \[\Delta x \cdot \Delta y = r \cdot \Delta r \Delta \theta\]

• 변화량이 scale이 \(r\) 이기 때문에 위 그림처럼 호의 반지름의 길이가 커질 수록 변화량이 커지는 것을 알 수 있습니다.

• 여기 까지 jacobian을 어떻게 행렬로 나타내는 지 배웠습니다. 그러면 실제 어떤 경우에 jacobian을 사용할 수 있을까요?
• 첫번째, partial derivative가 필요한 순간에 사용할 수 있습니다. jacobian 행렬의 각 element가 partial derivative를 수식이기 때문에 따로 계산할 것 없이 이 행렬에 값을 적용하는 것만으로 partial derivative 결과를 얻을 수 있습니다.
  • 특히 partial derivative가 필요한 대표적인 상황은 chain rule입니다. chain rule에서는 각 단계 별 first-order partial derivative한 vector/matrix의 곱을 하기 때문에, 이 때 많이 사용합니다.
• 두번째, 앞에서 설명한 것과 같이 linear transformation 하기 위함입니다. 우리가 다루는 많은 함수 식들은 non-linear 합니다. 이 non-linear 공간A를 공간B로 linear transformation할 때, jacobian 행렬을 사용할 수 있습니다.
• 이 때, 공간 A에서 공간 B로 transformation할 때, 그 변화량 만큼 곱을 해주게 되는데, 이 때 발생하는 변화량이 jacobian 행렬의 행렬식인 determinant가 됩니다.
  • jacobian 벡터에서는 변화량을 벡터로 구할 수 있었다면 jacobian 행렬에서는 변화량을 영역으로 구할 수 있습니다. (2차원에서는 면적이 되겠지요)

Sandpit 예제

• jacobian이 multivariate system의 gradient를 구한다는 것을 배웠습니다.
• 이 개념에 대한 좀 더 직관적인 이해를 돕기 위하여 지금부터 sandpit 이란 놀이(?)를 한번 해보도록 하겠습니다. (사실 coursera에서 혼자 놀아본 것일뿐… 블로그에서 기능이 제공되진 않습니다.)
• 그 전에 optimization이란 개념에 대하여 간단하게 다루어 보겠습니다. optimization은 가능한한 좋도록 하려는 의도로 일상 생활에서도 많이 쓰는 단어인데 공학에서 사용하는 optimization은 어떤 함수의 입력값이 들어갔을 때, 그 결과로 최댓값 또는 최솟값을 도출해 내는 것을 말합니다. 예를 들어 최단 거리를 구하는 것, 최소 비용을 구하는 것 또는 이익을 최대화 하는 것 등이 있습니다.
• 앞에서 다룬 예제를 다시 살펴보겠습니다.

• \[f(x, y) = e^{-(x^{2} + y^{2})}\]
• \[J = \begin{bmatrix} -2xe^{-(x^{2} + y^{2})}, & -2ye^{-(x^{2} + y^{2})} \end{bmatrix} = 0\]

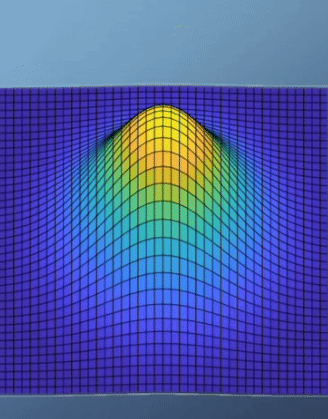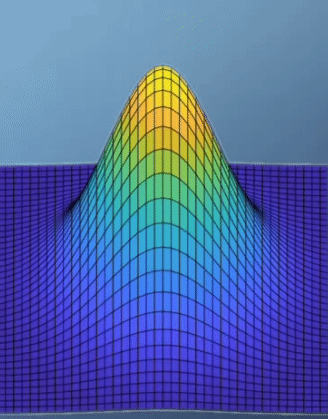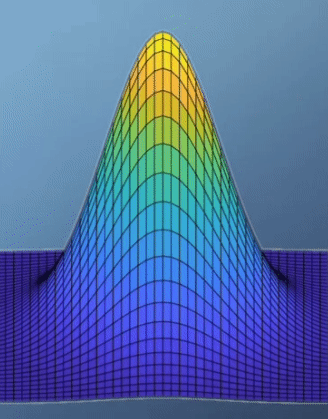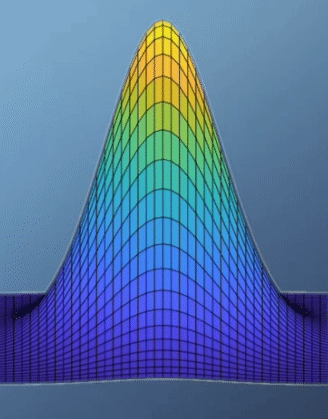
• 위 예제에서 optimal한 지점은 경사가 가장 최소가 되는 지점이 되도록 문제를 설정하는 것이 합당해 보입니다. 그리고 이 예제에서 경사가 가장 최소가 되는 지점에서 최댓값을 가지게 됩니다.

• 반면 식이 좀 복잡해 지기 시작하면 위 예제보다 함수 값 분포를 다루기가 까다로워집니다.

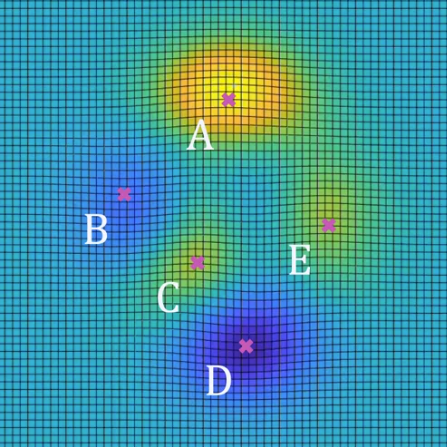
• 식이 복잡해 지면 경사가 최소가 되는 지점이 여러 군데 나타날 수 있습니다. 위 그림의 \(A, B, C, D, E\) 모두 경사가 최소가 되는 지점입니다. 하지만 값이 최대가 되는 지점 또는 최소가 되는 지점은 1군데 씩 있습니다.
• 예를 들어 \(A\)에서는 경사가 최소가 되고 또한 값은 최대가 되는 지점입니다. 이런 지점을 global maximum이라고 합니다. 반면 \(D\)에서는 경사가 최소가 되고 값 또한 최소가 되는 지점입니다. 이런 지점을 global minimum이라고 합니다. 나머지 부분은 local maximum/minimum이 되는 부분이 됩니다.

• 만약 임의의 어떤 지점에서 maximum/minimum 지점을 찾아가려면 어떻게 하면 될까요?
• 앞에서 다루었듯이 각 지점의 좌표를 jacobian 벡터에 대입하면 그 지점에서의 벡터값을 구할 수 있습니다. 그 벡터값의 크기와 방향을 변화가 큰 지 작은 지 알 수 있습니다.
• 모든 지점에서 벡터 형태로 나타내면 위 그림과 같이 나타낼 수 있습니다. 그러면 화살표 방향대로 이동만 하더라도 optimization을 할 수 있습니다.
• 하지만 화살표 방향만 따라가면 optimization은 되지만 그것이 항상 global optimization이 된다고는 보장할 수 없습니다. 사실 이 문제는 machine learning이 풀어야 할 숙제이기도 합니다.

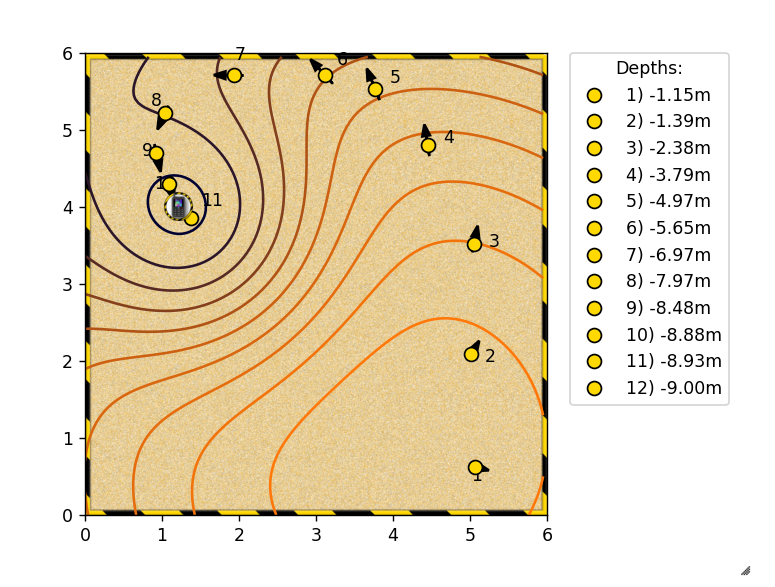
• 위 그림은 coursera에서 제공하는 실습 환경의 예제입니다. 그냥 단순히 jacobian 벡터에 좌표 값을 대입하면 벡터의 크기와 방향이 표시되고 그것을 이용하여 global minimum을 찾는 게임 입니다.
• 요점은 인간이 느끼는 이 optimization 방법을 machine learning에서도 똑같이 쓴다는 것입니다. 저희가 시각적으로 보고 판단한 것을 컴퓨터는 단순히 수치값으로만 해석한다는 차이점이 있을 뿐 접근 방법은 완전히 같습니다.

Hessian

• 이번에는 jacobian과 쌍으로 같이 소개되는 hessian에 대하여 다루어 보겠습니다. hessian 또한 multivariate system과 관련된 개념입니다.
• hessian을 단순히 말하면 jacobian 벡터의 확장이라고 말할 수 있습니다.
• jacobian에서는 어떤 함수 식의 1차 미분 한 결과를 벡터 형태로 모은 것(여기서 다루는 jacobian은 행렬이 아닌 벡터입니다.)인 반면 hessian은 jacobian 벡터를 한번 더 각 변수에 대하여 다시 한번 미분한 2차 미분의 결과를 모은 것입니다. 수식을 통해 보면 쉽게 이해하실 수 있습니다.

• \[H = \begin{bmatrix} \partial^{2} f / \partial x_{1}^{2} & \partial^{2} f / \partial x_{1}x_{2} & \cdots & \partial^{2} f / \partial x_{1}x_{n} \\ \partial^{2} f / \partial x_{2}x_{1} & \partial^{2} f / \partial x_{2}^{2} & \cdots & \partial^{2} f / \partial x_{2}x_{n} \\ \vdots & \vdots & \ddots & \vdots \\ \partial^{2} f / \partial x_{n}x_{1} & \partial^{2} f / \partial x_{n}x_{2} & \cdots & \partial^{2} f / \partial x_{n}^{2} \end{bmatrix}\]

• hessian 행렬을 보면 각 \((i, j)\)는 \(\partial^{2} f / \partial x_{i}x_{j}\)가 됨을 알 수 있습니다. 식을 보면 알 수 있겠지만 hessian 행렬은 대칭적인 것 또한 알 수 있습니다. (아래 예제를 참조하시기 바랍니다.)
• 따라서 hessian 행렬은 변수의 갯수가 \(n\)개일 때, \(n \times n\) 크기의 대칭 행렬이 됩니다.
• hessian을 손으로 구할 때에는 jacobian을 먼저 구한 다음에 jacobian의 결과를 가지고 행렬을 만들 수 있습니다. 한번 예제를 보겠습니다.

• \[f(x, y, z) = x^{2} y z\]
• \[J = \begin{bmatrix} 2xyz & x^{2}z & x^{2}y \end{bmatrix}\]
• \[H = \begin{bmatrix} 2yz & 2xz & 2xy \\ 2xz & 0 & x^{2} \\ 2xy & x^{2} & 0 \end{bmatrix}\]

• 그러면 hessian 행렬은 언제 사용할 수 있을까요?

• \[f(x,y) = x^{2} + y^{2}\]
• \[J = \begin{bmatrix} 2x & 2y \end{bmatrix}\]
• \[H = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}\]
• \[\vert H \vert = 4\]

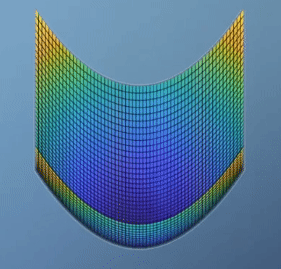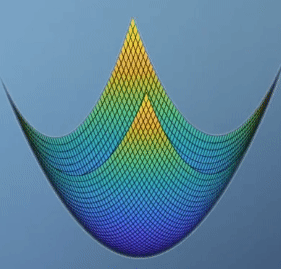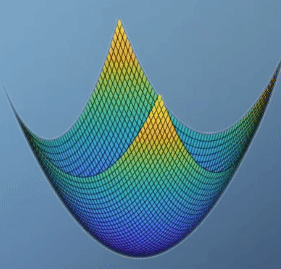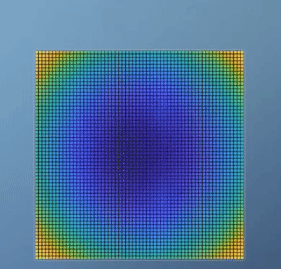
• hessian을 통하여 알 수 있는 것은 함수 \(f\)가 global optimization이 있는 형태인 지 그리고 있다면 global minimum인 지 global maximum인 지 판단해줍니다.
• 먼저 determinant가 양수이면 global optimization이 가능한 형태입니다.
• 그리고 hessian 행렬의 가장 왼쪽 상단의 값이 양수이면 global minimum을 가지게 됩니다. 반면 음수이면 global maximum을 가지게 됩니다.

• 반면 다음과 같은 예제를 한번 살펴보겠습니다.

• \[f(x, y) = x^{2} - y^{2}\]
• \[J = \begin{bmatrix} 2x & -2y \end{bmatrix}\]
• \[H = \begin{bmatrix} 2 & 0 \\ 0 & -2 \end{bmatrix}\]
• \[\vert H \vert = -4\]

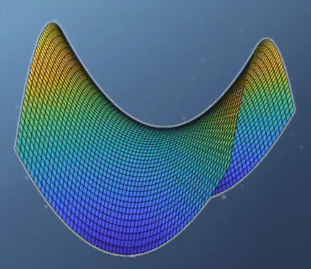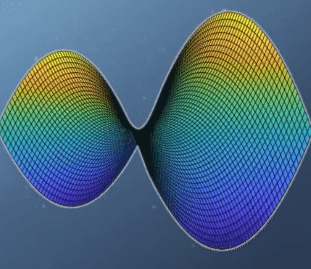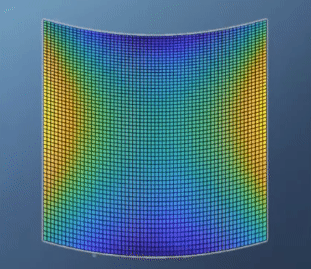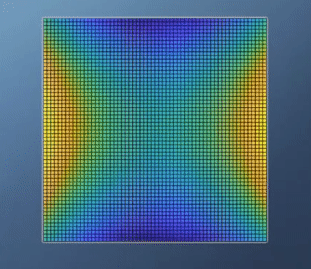
• 이 경우를 보면 앞의 예제와는 다르게 global optimization이 없습니다. 실제 값의 분포로도 알 수 있지만 hessian 행렬의 determinant를 보면 음수인 것을 통해서도 알 수 있습니다.
• 특히 위 그림과 같이 생긴 형태를 saddle point 라고 합니다. 이 경우가 optimization을 찾기 힘든 대표적인 예로 유명합니다. 왜냐하면 보는 관점에 따라서 minimum이기도 하고 maximum 이기도 하기 때문입니다.

Reality is hard

• 지금까지 다룬 내용을 살펴보면 optimization의 의미에 대하여 잘 이해하셨을 것이라 생각됩니다.
• optimization에 대한 직관적 이해를 위하여 지금 까지 3차원의 데이터만을 이용하였습니다. 즉, x축 y축 그리고 z축 또는 컬러 이렇게만 이용하였기 때문에 변화량에 대해서 시각적으로 경사 형태로 표현할 수 있었습니다.
• 하지만 실제 현실 세계의 문제를 최적화 하는 데에는 크게 3가지 문제점이 존재합니다.

• ① 차원의 수가 많은 문제입니다.
• 실제 존재하는 최적화 문제, 특히 뉴럴 네트워크 같은 문제에서는 차원의 갯수가 수천, 수만개가 됩니다.
• 이런 경우에는 단순히 시각화 해서 optimization 점을 확인하는 것은 불가능 합니다.
• 따라서 앞에서 다룬 예제(2차원 평면에 색을 통하여 값을 표시한 것)에서의 직관적인 이해를 고차원 케이스에 접목시켜서 이해할 필요가 있습니다.

• ② 함수식에 따라 계산량이 많을 수 있습니다.
• 앞에서 다룬 예제들의 수식을 보면 상당히 간단한 수식들 입니다. 하지만 실제 문제들의 수식이 예제들 처럼 간단한 경우는 잘 없습니다.
• 수식이 매우 복잡한 경우에는 모든 점들에 대하여 계산을 통해 optimization을 한다는 것은 상당히 비효율적입니다.

• ③ 함수식의 데이터 분포가 깔끔하지 않을 수 있습니다.
• 앞에서 다룬 예제들의 데이터 분포를 보면 매끄러운 산을 오르 내리는 듯한 형상을 가집니다. 하지만 현실 문제들이 모두 이렇진 않습니다.
• 예를 들어 부드럽게 global maximum/minimum으로 이동할 수 있는 형태가 아니라 노이즈가 많이 낀 울퉁 불퉁한 형태의 데이터 분포가 나타났다고 가정하면 local optima 지점으로 인해 global optima 지점으로 도달하기가 어려워지는 문제가 있습니다..

• 여기까지 배운 것의 키워드는 total derivative, jacobian, hessian 입니다.
• 계산을 하는 것은 울프람 알파, 매트랩, 파이썬 어떤 것을 이용하더라도 쉽게 계산할 수 있기 때문에 계산이 문제가 되지 않습니다.
• 하지만 각 키워드의 의미와 어떻게 활용할 지에 대하여 고민을 하는 것에는 충분한 가치가 있습니다.

mathematics for machine learning 글 목록