multivariate chain rule과 applications

mathematics for machine learning 글 목록

이 글은 Coursera의 Mathematics for Machine Learning: Multivariate Calculus 을 보고 정리한 내용입니다.
이번 글에서는 앞에서 다룬 charin rule을 multivariate 환경으로 확장을 하고 neural network에 접목을 시켜보겠습니다.

multivariate chain rule

앞의 글에서 배운 total derivative에 대하여 간략한 예제를 살펴보겠습니다.

\[f(x, y, z) = \sin{(x)} \cdot exp(yz^{2})\]
\[x = t - 1, \quad y = t^{2}, \quad z = \frac{1}{t}\]
\[\frac{\text{d}f}{\text{d}t} = \frac{\text{d}f}{\text{d}x}\frac{\text{d}x}{\text{d}t} + \frac{\text{d}f}{\text{d}y}\frac{\text{d}y}{\text{d}t} + \frac{\text{d}f}{\text{d}z}\frac{\text{d}z}{\text{d}t}\]
\[\frac{\text{d}f}{\text{d}t} = \cos{(t-1)}e\]

total derivative의 내용을 요약하면 chain rule 형태의 multivariate derivative에서는 각 변수의 partial derivative를 통해 분해한 뒤, chain rule을 적용할 수 있고 그 결과를 모두 합하면 된다는 내용입니다.

이것을 좀 더 일반화한 식으로 적어보도록 하겠습니다.

\[f(x) = f(x_{1}, x_{2}, \cdots , x_{n})\]

\[\frac{\partial f}{\partial x} = \begin{bmatrix} \partial f / \partial x_{1} \\ \partial f / \partial x_{2} \\ \partial f / \partial x_{3} \\ \vdots \\ \partial f / \partial x_{n} \end{bmatrix} \quad \frac{\text{d} x}{\text{d} t} = \begin{bmatrix} \text{d} x_{1} / \text{d} t \\ \text{d} x_{2} / \text{d} t \\ \text{d} x_{3} / \text{d} t \\ \vdots \\ \text{d} x_{n} / \text{d} t \end{bmatrix}\]

\[\frac{\text{d}f}{\text{d}t} = \frac{\partial f}{\partial x} \cdot \frac{\text{d}x}{\text{d}t}\]

위 식처럼 inner product 형태로 나타내면 total derivative를 간단하게 표현할 수 있습니다.

그러면 multivariate chain rule에 대하여 조금만 더 자세히 살펴보도록 하겠습니다.
앞의 예제와 같은 형태로 함수가 있다고 가정해 보겠습니다. $f(x)$는 함수이고 $x$는 변수 $t$에 dependent 한 벡터입니다.
그러면 $f(x(t))$ 형태로 적을 수 있습니다. 여기서 independent한 변수는 $t$이므로 결국 관심이 있는 것은 $t$의 변화에 대한 함수 $f$의 변화를 알고 싶은 것이 derivative의 목적입니다. 그러면 다음과 같이 compact 하게 쓸 수 있습니다.

\[\frac{\text{d}f}{\text{d}t} = \frac{\partial f}{\partial x} \cdot \frac{\text{d}x}{\text{d}t}\]

그리고 $\partial f / \partial x$에서 $x$는 vector이므로 $(x_{1}, x_{2}, \cdots , x_{n})$의 형태를 가지게 됩니다.
이 글의 윗 부분에서도 column vector 형식으로 $\partial f / \partial x$을 표현하였는데, 앞의 글에서 배운 jacobian에 대입해서 보면 transpose한 형태가 됩니다.

\[\frac{\partial f}{\partial x} = \begin{bmatrix} \partial f / \partial x_{1} \\ \partial f / \partial x_{2} \\ \partial f / \partial x_{3} \\ \vdots \\ \partial f / \partial x_{n} \end{bmatrix} = (J_{f})^{T}\]

따라서 위 식의 column vector의 inner product 또한 다음과 같이 row vector와 column vector의 곱으로 표현할 수 있습니다.

\[\frac{\text{d}f}{\text{d}t} = J_{f} \frac{\text{d}x}{\text{d}t}\]

chain rule은 말 그대로 여러 단계에 걸쳐서 연쇄(chain)적으로 적용 가능합니다. 먼저 아래 예제에서 univariate 케이스 & 2단계 chain rule을 적용한 케이스에 대해서 살펴보겠습니다.

\[f(x) = 5x \\ x(u) = 1 - u \\ u(t) = t^{2}\]
\[\color{red}{f(t) = 5(1-t^{2}) = 5 - 5t^{2}}\]
\[\color{red}{\frac{\text{d}f}{\text{d}t} = -10t}\]
\[\begin{split} \color{blue}{\frac{\text{d}f}{\text{d}t}} &= \color{blue}{\frac{\text{d}f}{\text{d}x}\frac{\text{d}x}{\text{d}u}\frac{\text{d}u}{\text{d}t}} \\ &= \color{blue}{(5)(-1)(2t) = -10t} \end{split}\]

대입을 하여 미분을 한 경우와 chain rule을 이용하여 미분을 한 경우 동일한 결과를 얻을 수 있습니다. 따라서 univariate에서 2단계, 3단계, 또는 n단계의 chain rule을 이용하여 미분을 하는 것과 일일이 대입해서 미분을 하는 것의 결과는 같습니다.
물론 이 글의 목적처럼 multivariate에서도 chain rule을 적용하면 2단계, 3단계, n단계 까지 모두 적용가능합니다. 한번 살펴보겠습니다. 이번에는 multivariate입니다.

\[f(x(u(t)))\]
\[\color{orange}{f(x) = f(x_{1}, x_{2})}\]
\[\color{green}{x(u) = \begin{bmatrix} x_{1}(u_{1}, u_{2}) \\ x_{2}(u_{1}, u_{2}) \end{bmatrix}}\]
\[\color{purple}{u(t) = \begin{bmatrix} u_{1}(t) \\ u_{2}(t) \end{bmatrix}}\]

위 식을 정리해 보면, $x = (x_{1}, x_{2})$로 벡터이고, $u = (u_{1}, u_{2})$로 벡터입니다. 용어로 나타내면 $x$와 $u$는 vector valued function 이라고 합니다.
함수의 independent한 변수인 $t$가 scalar input이라 하고 함수의 출력 또한 scalar output이라고 하면 univariate 케이스와 동일하게 표현할 수 있습니다.

\[\frac{\text{d}f}{\text{d}t} = \color{orange}{\frac{\partial f}{\partial x}} \color{green}{\frac{\partial x}{\partial u}}\color{purple}{\frac{\text{d}u}{\text{d}t}}\]

따라서 chain rule을 적용하여 계산한 결과를 보면 다음과 같습니다.

\[\frac{\text{d}f}{\text{d}t} = \color{orange}{\frac{\partial f}{\partial x}} \color{green}{\frac{\partial x}{\partial u}}\color{purple}{\frac{\text{d}u}{\text{d}t}} = \color{orange}{\begin{bmatrix} \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}} \end{bmatrix}} \color{green}{\begin{bmatrix} \frac{\partial x_{1}}{\partial u_{1}} & \frac{\partial x_{1}}{\partial u_{2}} \\ \frac{\partial x_{2}}{\partial u_{1}} & \frac{\partial x_{2}}{\partial u_{2}} \end{bmatrix}} \color{purple}{\begin{bmatrix} \frac{\text{d}u_{1}}{\text{d}t} \\ \frac{\text{d}u_{2}}{\text{d}t} \end{bmatrix}}\]

연산의 각 shape을 살펴보면 $(1 \times 1) = \color{orange}{(1 \times 2)}\color{green}{(2 \times 2)}\color{purple}{(2 \times 1)}$ 가 됩니다.
특히, 유심히 봐야할 것은 각 단계를 보면 모두 jacobian (벡터/행렬) 이라는 것입니다.
앞의 글에서 배운 jacobian이 chain rule에서 얼마나 잘 활용되는 지 이해하셨으면 여기 까지의 핵심을 잘 따라오신 것입니다.

neural network

21세기는 가히 머신 러닝의 시대라고 말할 수 있습니다. 특히 neural network의 시대가 밝아진 것이지요.
지금부터는 간단한 neural network를 살펴보면서 앞에서 배운 multivariate chain rule이 어떻게 사용되는 지 알아보도록 하겠습니다.
이 글의 초점은 multivariate chain rule의 neural network에서의 역할입니다. neural netowork에 대하여 알고 싶으시면 다음 링크를 참조하시기 바랍니다.
- 링크 : https://gaussian37.github.io/dl-concept-table/
따라서 이번 글에서는 기본적인 neural network의 형태인 dnn(deep neural network)을 다룰 것이고 이는 단순히 fully connected 방식으로 연결한 구조입니다. 이 구조가 가장 간단하면서도 multivariate chain rule를 설명하기 용이합니다. 그러면 시작하겠습니다.

$Drawing$

neural network가 하는 역할은 무궁무진 하지만, 사실 단순한 함수에 불과합니다. input이 있고 그 input에 대하여 처리를 한 다음에 output을 만들어 내는 말 그대로 함수입니다.
위 그림에서 원을 neuron 이라고 합니다. 선이 각각의 neuron을 이어주는 역할을 합니다.

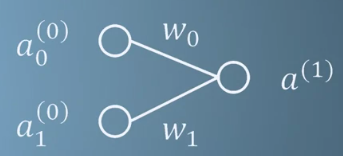
$Drawing$

예를 들어 $a^{(0)}$ neuron 에서 $a^{(1)}$의 neuron으로 연결이 되었다면, 이 연결을 수식으로 나타내면 다음과 같습니다.

\[a^{(1)} = \sigma(wa^{(0)} + b)\]
\[a \Rightarrow \text{"activity"}\]
\[w \Rightarrow \text{"weight"}\]
\[b \Rightarrow \text{"bias"}\]
\[\sigma \Rightarrow \text{"activation function"}\]

각 기호의 역할을 간단히 적으면 $a$가 input, $w$는 위의 neuron을 연결해 주는 선의 역할로 weight 값이고 역할은 input에 곱해지는 역할입니다. $w$가 곱해지는 값이라면 $b$는 더해지는 값으로 bias 입니다.
마지막으로 $\sigma$는 이 neuron이 켜질 지, 꺼질 지 결정하는 함수입니다. 실제 사람의 신경 세포도 전기적 신호에 따라서 반응을 하거나 안하거나 선택이 됩니다. 수많은 neuron들이 동시에 반응을 하고 이 조합들을 통해 어떤 판단을 하게됩니다. 여기서 반응을 하거나 안하거나 선택하는 것은 마치 threshold 역할을 하는 것처럼 보입니다. $\sigma$ 함수는 threshold 역할을 합니다. 이렇게 threshold를 넘었을 때와 넘지 못했을 때를 활성화/비활성화 라는 용어를 사용하여 neuron이 켜지는 지 꺼지는 지를 나타내기 때문에 activation function이라고 합니다.
- 다양한 activation function을 참조 하시기 바랍니다.
- 링크 : https://gaussian37.github.io/dl-concept-activation_functions/

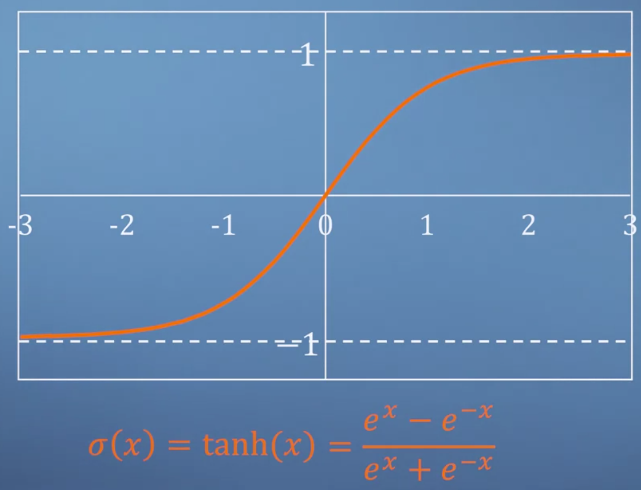
$Drawing$

위 그림은 대표적인 activation function 중의 하나인 tanh로 0을 기준으로 함수 값이 양수 / 음수로 나뉘게 됨을 볼 수 있습니다.
이처럼 $\sigma$는 non-linear function의 형태를 가집니다. 왜냐하면 이러한 non-linear function이 중간에 적용되지 않으면 계속 linear transformation만 발생하기 때문입니다. 즉, linear classifier 밖에 할 수 없게 되기 때문에 항상 $\sigma$는 non-linear function을 사용합니다.
지금까지 neural network에서 사용하는 기호인 $a^{(i)}, w, b, \sigma$에 대하여 알아보았습니다.
지금부터는 neuron을 좀 더 사용해 보도록 하겠습니다.

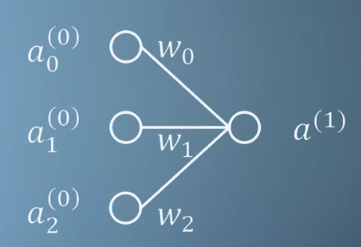
$Drawing$

위 그림과 같은 neuron을 구성하면 그 식은 다음과 같이 확장됩니다.

\[a^{(1)} = \sigma(w_{0}a_{0}^{(0)} + w_{1}a_{1}^{(0)} + b)\]

$Drawing$

\[a^{(1)} = \sigma(w_{0}a_{0}^{(0)} + w_{1}a_{1}^{(0)} + w_{2}a_{2}^{(0)} + b)\]

즉, neuron이 추가될 수록 $w_{j}a_{j}^{(i)}$만 추가되면 됩니다. 일반화 시키면 다음과 같습니다.

\[\sigma \Biggl(\biggl(\sum_{j=0}^n w_{j}a_{j}^{(i)} \biggr) + b \Biggr) = \sigma(w \cdot a(i) + b)\]

이번에는 출력 neuron의 갯수를 한 개 더 늘려보겠습니다. 여기서 $w_{i}$는 벡터입니다.

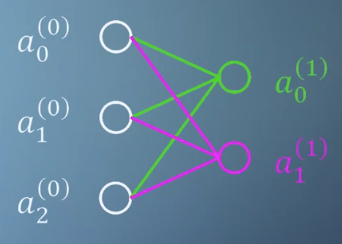
$Drawing$

\[\color{lime}{a_{0}^{(1)}} = \sigma(\color{lime}{w_{0}} \cdot a^{0} + \color{lime}{b_{0}})\]
\[\color{fuchsia}{a_{1}^{(1)}} = \sigma(\color{fuchsia}{w_{1}} \cdot a^{0} + \color{fuchsia}{b_{1}})\]
\[a^{(1)} = \sigma(W^{(1)} \cdot a^{(0)} + b^{(1)})\]

출력의 neuron 갯수가 추가됨에 따라 $W$는 matrix로 $b$는 vector가 된 것을 확인할 수 있습니다.

$Drawing$

지금 까지 배운 내용을 일반화 시키면 위와 같이 정리할 수 있습니다.
위 슬라이드는 조금 헷갈릴 수도 있어서 간략하게 설명해 보겠습니다. 먼저 $a_{n}^{(l)}$는 $l$ 번째 layer의 $n$번째 노드 입니다. 단순하게 $a^{(l)}$로 표시하면 이는 $a_{0}^{(l)}$ 부터 $a_{n}^{(l)}$ 까지의 값을 가지는 벡터가 됩니다.
이와 유사하게 $b_{n}^{(l)}$는 $l - 1$번째 layer에서 $l$ 번째 layer를 연결할 때 사용하는 bias로 아랫 첨자와 윗 첨자에 대한 의미는 노드와 같습니다. $b^{(l)}$는 $l-1$번째 layer 노드를 이용하여 $l$번째 layer를 연산할 때 사용되는 bias 벡터가 됩니다.
조금 헷갈리는 점은 $w_{j,i}^{(l)}$입니다. 이는 $a_{j}^{(l-1)}$ 과 $a_{i}^{(l)}$을 잇는 weight 입니다. 이 모든 weight 들을 한번에 표시한 $W^{(l)}$은 weight 행렬이 됩니다.
예를 들어 $a_{0}^{1}$을 살펴보겠습니다.

\[a_{0}^{1} = \sigma(w_{0,0}^{(1)}a_{0}^{0} + w_{0,1}^{(1)}a_{1}^{0} + \cdots + w_{0,n-1}^{(1)}a_{n-1}^{0} + b_{0}^{(1)})\]

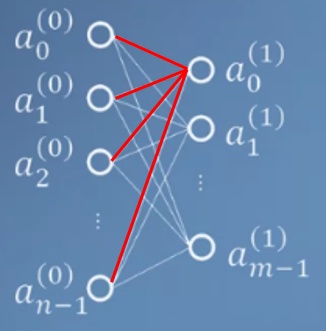
$Drawing$

식으로 표현한 node, weight는 그림의 빨간색 선과 이어진 노드입니다. 노드의 인덱스가 $j \to i$ 로 연결되어 있다는 점만 유의해서 보시면 됩니다.

마지막으로 추가해 볼 것은 layer 입니다.

$Drawing$

\[\color{fuchsia}{a^{(1)}} = \sigma(W^{(1)} \cdot a^{(0)} + b^{(1)} )\]
\[a^{(2)} = \sigma(W^{(2)} \cdot \color{fuchsia}{a^{(1)}} + b^{(2)} )\]

최종적으로 input, layer, output을 모두 고려한 일반화를 하면 식은 다음과 같습니다.

\[a^{(L)} = \sigma(W^{(L)} \cdot a^{(L-1)} + b^{(L)})\]

여기서 $a^{(L)}$과 $a^{(L-1)}$의 크기는 풀려고 하는 문제에 따라 다를 수 있습니다. 즉, 처음 모델링 할 때 정해주어야 하는 것입니다.
하지만 $W$와 $b$의 크기는 $a$에 따라 정해집니다. 그 이유는 위 그림들을 보면 알 수 있습니다.
- ① $W^{(L)}$의 크기 : $\text{number of neuron in } a^{(L-1)} \times \text{number of neuron in } a^{(L)}$
- ② $b^{(L)}$의 크기 : $\text{number of neuron in } a^{(L)}$

training neural network

지금까지 neural network의 간단한 개념에 대하여 다루어 보았고 이를 hidden layer를 포함한 fully connected feed forward network 형태로 나타내 보았습니다. (앞에서 노드를 왼쪽에서 오른쪽으로 연결한 형태의 기본적인 네트워크 형태입니다.)
여기서 성능을 좌우하는 것은 weight와 bias 입니다. 왜냐하면 input에 어떤 weight가 곱해지고 bias가 더해지느냐에 따라서 최종 output이 달라지기 때문입니다.
그러면 풀려고 하는 문제에 따라서 weight와 bias가 최적이 되도록 잘 셋팅을 해주어야 하는데, 이 과정을 training 이라고 합니다. 어떻게 하면 될까요?
대표적인 training의 방법은 back propagation 입니다. 이렇게 부르는 이유는 학습의 시작을 output 뉴런부터 시작해서 input 뉴런 방향으로 역으로 접근하기 때문입니다.

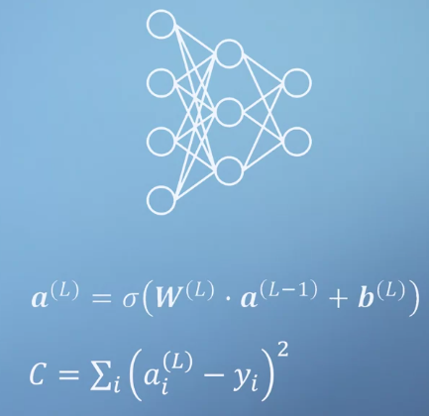
$Drawing$

위 그림에서 주목할 점은 마지막 식 $C$ 입니다. 여기서 $a_{i}^{(L)}$을 마지막 layer의 output 이라고 하면 그 아웃풋에 해당하는 정답 label이 있다고 가정하겠습니다. 그것이 바로 $y_{i}$ 입니다.
따라서 $C$는 output과 label이 얼만큼의 차이가 있는지 제곱합을 하는 식입니다. 0에 가까울 수록 오차가 작다고 말할 수 있습니다.

앞에서 언급한 바와 같이 변화가 필요한 것은 weight와 bias 입니다. 특히 weight의 영향이 굉장히 크므로 weight에 따라 cost가 어떻게 변하는 지 관찰해 보겠습니다.
아래는 단순한 아래로 볼록한 그래프로 최솟값을 가지는 지점이 한 군데인 아주 심플한 형태의 weight와 cost 그래프 입니다.

$Drawing$

왼쪽 그래프의 $w_{0}$ 지점에서 미분을 하면 양의 변화량을 가짐을 알 수 있습니다. 궁극적으로 도달해야 하는 weight의 위치는 미분의 값이 0인 지점으로 변화량이 없는 곳입니다. 즉, 극소 지점입니다. 따라서 변화량과 반대 방향으로 weight를 변경해 줍니다. 따라서 오른쪽 그래프 처럼 변화량과 반대 방향으로 weight를 이동시켜야 합니다. (화살표의 방향이 바뀐 것을 확인하실 수 있습니다.)

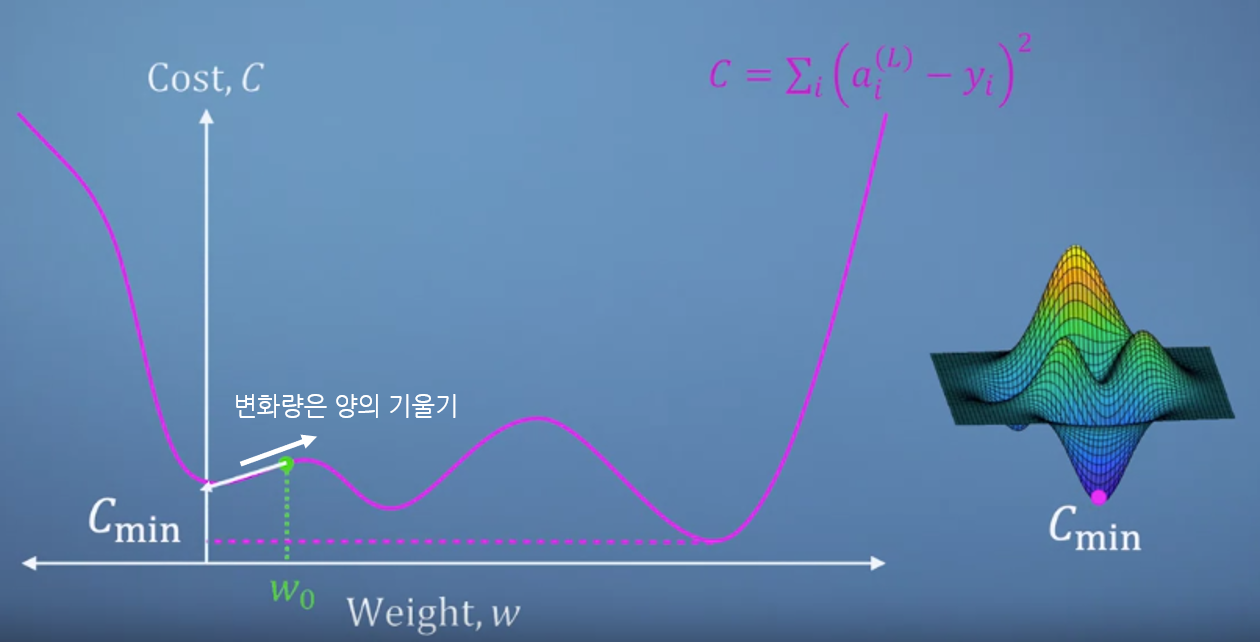
$Drawing$

하지만 위 그림과 같이 local minima인 지점이 여럿 생기게 된다면 global minima 방향이 아닌 잘못된 방향으로 weight를 변경할 수 있는 문제가 발생하기도 합니다. (어려운 문제긴 하지만 다양한 개선책들이 많이 있습니다. 제 블로그에도…)
중요한 것은 이 계산을 하기 위해서는 미분을 해야 한다는 것이고 위의 neural network와 같이 weight의 갯수가 많은 상황에서는 ($w_{0}, w_{1}, ...$) 각 weight에 따른 jacobian을 구해야 한다는 것입니다. 즉, 모든 weight (변수)에 관하여 partial derivative를 하고 그 변화량과 반대 방향으로 weight 값을 변경해주어야 한다는 것이 핵심입니다.
각 변수에 대하여 jacobian을 구하였다면 chain rule을 이용하여 전체 변화량을 계산할 수 있습니다. 다음 예제를 살펴보겠습니다.

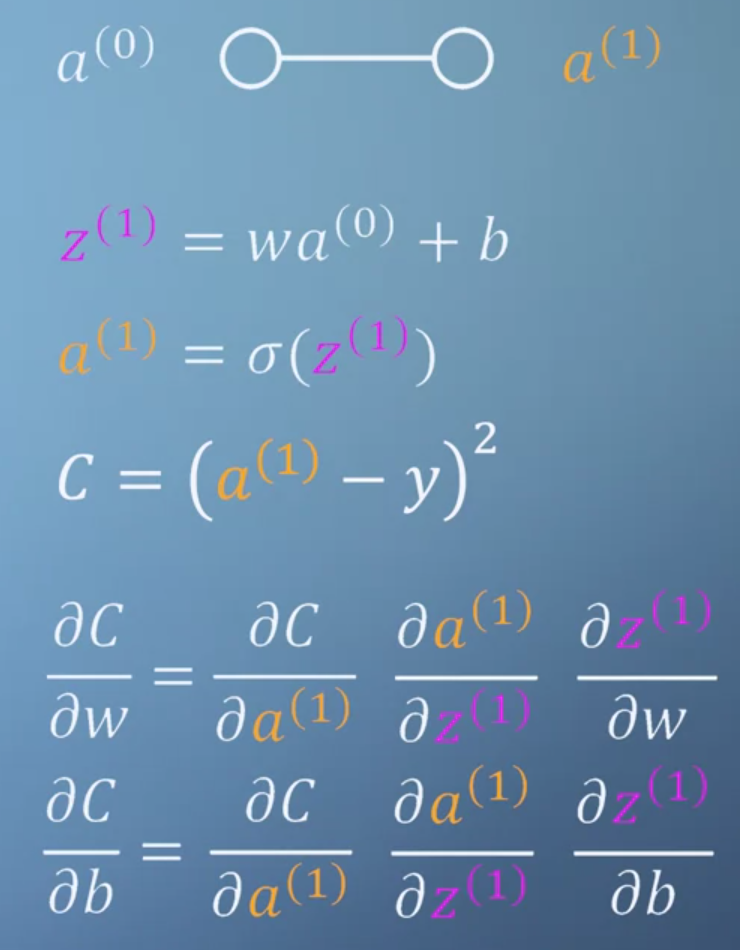
$Drawing$

위 식을 보면 최종 output은 $C$이고 변수는 $w, b$ 이므로 각 변수 $w, b$에 대하여 partial derivative를 구해주어야 합니다.
따라서 위 식과 같이 partial derivative인 $\partial C / \partial w$ 와 $\partial C / \partial b$를 chain rule을 통해 구할 수 있습니다.
앞에서 말했듯이 output에서 시작하여 intput 뉴런 방향으로 각 변수에 대하여 chain rule을 통해 미분값을 구하므로 이 과정을 back propagation 이라고 합니다.

backpropagation practice

이번에는 앞에서 배운 backpropagation을 파이썬 코드를 이용하여 다루어 보도록 하겠습니다.
파이썬의 numpy를 사용해서 행렬 연산을 해보겠습니다. 먼저 numpy의 A * B는 element-wise multiplication을 나타내고 A @ B 는 matrix multiplication을 나타냅니다.

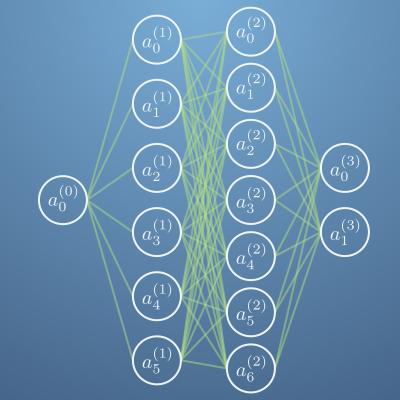
$Drawing$

다루어 볼 예제는 위 그림과 같은 구조의 네트워크입니다. 2개의 hidden layer가 있고 첫번째 hidden layer는 6개의 node가 있고 두번째 hidden layer는 7개의 node가 있는 상태입니다.
또한 이번 예제에서 사용해 볼 activation function은 sigmoid 입니다. 수식을 정리하면 다음과 같습니다.

\[a^{(z)} = \sigma(z^{(n)})\]
\[z^{(n)} = W^{(n)}a^{(n-1)} + b^{(n)}\]
\[\sigma^{(z)} = \frac{1}{exp(-z)}\]
\[\frac{d\sigma^{(z)}}{dz} = \frac{exp(-z)}{(exp(-z) + 1)^{2}}\]

import numpy as np
import matplotlib.pyplot as plt

sigma = lambda z : 1 / (1 + np.exp(-z))
d_sigma = lambda z : np.exp(-z) / (np.exp(-z) + 1)**2

# 네트워크를 구조로 초기화하고 이미 수행 한 모든 훈련을 재설정합니다.
def reset_network (n1 = 6, n2 = 7, random=np.random) :
    global W1, W2, W3, b1, b2, b3
    W1 = random.randn(n1, 1)
    W2 = random.randn(n2, n1)
    W3 = random.randn(2, n2)
    b1 = random.randn(n1, 1)
    b2 = random.randn(n2, 1)
    b3 = random.randn(2, 1)

# 각 activation을 다음 계층으로 전달합니다. 모든 weighted sum과 activation을 반환합니다.
def network_function(a0) :
    z1 = W1 @ a0 + b1
    a1 = sigma(z1)
    z2 = W2 @ a1 + b2
    a2 = sigma(z2)
    z3 = W3 @ a2 + b3
    a3 = sigma(z3)
    return a0, z1, a1, z2, a2, z3, a3


def cost(x, y) :
    return np.linalg.norm(network_function(x)[-1] - y)**2 / x.size

back propagation을 하기 위해 weight와 bias에 대하여 jacobian을 구해야합니다.

\[J_{w^{(3)}} = \frac{\partial C}{\partial W^{(3)}}\]
\[J_{b^{(3)}} = \frac{\partial C}{\partial b^{(3)}}\]
\[C = \frac{1}{N} \sum_{k}C_{k}\]

weight에 대하여 partial derivative를 하기 위해 chain rule을 사용해 보도록 하겠습니다.

\[\frac{\partial C}{\partial W^{(3)}} = \frac{\partial C}{\partial a^{(3)}}\frac{\partial a^{(3)}}{\partial z^{(3)}}\frac{\partial z^{(3)}}{\partial W^{(3)}}\]

bias에 대하여 partial derivative를 해보겠습니다. 방법은 weight에 대한 partial derivative와 같습니다.

\[\frac{\partial C}{\partial b^{(3)}} = \frac{\partial C}{\partial a^{(3)}}\frac{\partial a^{(3)}}{\partial z^{(3)}}\frac{\partial z^{(3)}}{\partial b^{(3)}}\]

각각의 partial derivative는 다음 식을 따릅니다.

\[\frac{C}{\partial a^{(3)}} = 2(a^{(3)} - y)\]
\[\frac{\partial a^{(3)}}{\partial z^{(3)}} = \sigma'(z^{(3)})\]
\[\frac{\partial z^{(3)}}{\partial W^{(3)}} = a^{(2)}\]
\[\frac{\partial z^{(3)}}{\partial b^{(3)}} = 1\]

그러면 위 식을 이용하여 $J_{w^{(3)}}$을 구해보도록 하겠습니다.

# 3번째 layer의 weight를 위한 jacobian 입니다.
def J_W3 (x, y) :
    # 먼저 네트워크의 각 계층에서 모든 activation 및 weighted sum을 가져옵니다.
    a0, z1, a1, z2, a2, z3, a3 = network_function(x)
    # 변수 J를 사용하여 결과의 일부를 저장하고 각 줄에서 업데이트합니다.
    # 먼저, 위 식을 사용하여 dC / da3을 계산합니다.
    J = 2 * (a3 - y) / x.size
    # 다음으로 우리가 계산 한 결과에 da3 / dz3 = d_sigma(z3) 을 곱해줍니다.
    J = J * d_sigma(z3)
    # 그런 다음 최종 편미분으로 내적을 취합니다. dz3 / dW3 = a2
    J = J @ a2.T
    return J

# 이 함수에서는 bias에 대한 자코비안을 구현합니다.
# partial derivative에서 볼 수 있듯이 마지막 partial derivative만 다릅니다.
# 처음 두 부분 partial derivative는 이전과 동일합니다.
def J_b3 (x, y) :
    a0, z1, a1, z2, a2, z3, a3 = network_function(x)
    J = 2 * (a3 - y) / x.size
    J = J * d_sigma(z3)
    # 마지막 줄에는 dz3 / db3을 곱할 필요가 없습니다. 왜냐하면 1을 곱하기 때문입니다.
    J = np.sum(J, axis=1, keepdims=True)
    return J

다음으로 2번 layer를 위한 jacobian을 구해보도록 하겠습니다. partial derivative는 다음과 같습니다.

\[\frac{\partial C}{\partial W^{(2)}} = \frac{\partial C}{\partial a^{(3)}} \Biggl( \frac{\partial a^{(3)}}{\partial a^{(2)}} \Biggr) \frac{\partial a^{(2)}}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial W^{(2)}}\]
\[\frac{\partial C}{\partial b^{(2)}} = \frac{\partial C}{\partial a^{(3)}} \Biggl( \frac{\partial a^{(3)}}{\partial a^{(2)}} \Biggr) \frac{\partial a^{(2)}}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial b^{(2)}}\]

이 식은 다음 2가지를 제외하면 앞 식과 같습니다.
① $a^{(3)} / a^{(2)}$
② $a^{(3)} / a^{(2)}$ 뒤의 term 부터는 앞 식에 비해 한 단계 낮은 layer를 다룹니다.

그리고 $a^{(3)} / a^{(2)}$ 의 식은 다음과 같이 전개 될 수 있습니다.

\[\frac{\partial a^{(3)}}{\partial a^{(2)}} = \frac{\partial a^{(3)}}{\partial z^{(3)}} \frac{\partial z^{(3)}}{\partial a^{(2)}} = \sigma'(z^{(3)}) W^{(3)}\]

왜냐하면 $a^{n)} = \sigma(z^{(n)})$ 이고 ${a}^{(n)} = \sigma(z^{(n)})$ 이기 때문에 각 term은 다음과 같이 풀어지기 때문입니다.

\[\frac{\partial a^{(3)}}{\partial z^{(3)}} = \sigma'(z^{(3)})\]
\[\frac{\partial z^{(3)}}{\partial a^{(2)}} = W^{(3)}\]
\[\frac{\partial a^{(3)}}{\partial z^{(3)}}\frac{\partial z^{(3)}}{\partial a^{(2)}} = \sigma'(z^{(3)})W^{(3)} = \frac{a^{(3)}}{a^{(2)}}\]

def J_W2 (x, y):
    a0, z1, a1, z2, a2, z3, a3 = network_function(x)
    J = 2 * (a3 - y) / x.size
    
    # 다음 2 줄은 da3 / da2 = σ'(z3)*W3 을 구현하는 것입니다.
    J = J * d_sigma(z3)
    J = (J.T @ W3).T

    # 앞에서 다룬 J_W3과 같은 방법으로 전개하지만 layer의 수가 줄어든 차이가 있습니다.
    J = J * d_sigma(z2)
    J = J @ a1.T 
    return J


def J_b2 (x, y) :
    a0, z1, a1, z2, a2, z3, a3 = network_function(x)
    J = 2 * (a3 - y) / x.size
    J = J * d_sigma(z3)
    J = (J.T @ W3).T
    J = J * d_sigma(z2)
    J = np.sum(J, axis=1, keepdims=True) 
    return J

이제 첫번째 layer의 weight와 bias를 이용하여 partial derivative를 해보겠습니다. 방법은 앞에서 한 것과 같습니다.

\[\frac{\partial C}{\partial W^{(1)}} = \frac{\partial C}{\partial a^{(3)}} \left( \frac{\partial a^{(3)}}{\partial a^{(2)}} \frac{\partial a^{(2)}}{\partial a^{(1)}} \right) \frac{\partial a^{(1)}}{\partial z^{(1)}} \frac{\partial z^{(1)}}{\partial W^{(1)}}\]
\[\frac{\partial C}{\partial b^{(1)}} = \frac{\partial C}{\partial a^{(3)}} \left( \frac{\partial a^{(3)}}{\partial a^{(2)}} \frac {\partial a^{(2)}}{\partial a^{(1)}} \right) \frac{\partial a^{(1)}}{\partial z^{(1)}} \frac{\partial z^{(1)}}{\partial b^{(1)}}\]

def J_W1 (x, y) :
    a0, z1, a1, z2, a2, z3, a3 = network_function(x)
    J = 2 * (a3 - y) / x.size
    J = J * d_sigma(z3)
    J = (J.T @ W3).T
    J = J * d_sigma(z2)
    J = (J.T @ W2).T
    J = J * d_sigma(z1)
    J = J @ a0.T
    return J

def J_b1 (x, y) :
    a0, z1, a1, z2, a2, z3, a3 = network_function(x)
    J = 2 * (a3 - y) / x.size
    J = J * d_sigma(z3)
    J = (J.T @ W3).T
    J = J * d_sigma(z2)
    J = (J.T @ W2).T
    J = J * d_sigma(z1)
    J = np.sum(J, axis=1, keepdims=True)
    return J

나머지 아래 부분은 실습을 하기 위한 데이터 생성 부분과 학습을 위한 코드입니다.

import numpy as np
import matplotlib.colors as mcolors
import matplotlib.pyplot as plt

def plot_training (x, y, iterations=10000, aggression=3.5, noise=1) :
    global W1, W2, W3, b1, b2, b3
    fig,ax = plt.subplots(figsize=(8, 8), dpi= 80)
    ax.set_xlim([0,1])
    ax.set_ylim([0,1])
    ax.set_aspect(1)

    xx = np.arange(0,1.01,0.01)
    yy = np.arange(0,1.01,0.01)
    X, Y = np.meshgrid(xx, yy)
    Z = ((X-0.5)**2 + (Y-1)**2)**(1/2) / (1.25)**(1/2)
    im = ax.imshow(Z, vmin=0, vmax=1, extent=[0, 1, 1, 0], cmap=blueMap)

    ax.plot(y[0],y[1], lw=1.5, color=green);

    while iterations>=0 :
        W1 = W1 - J_W1(x, y) * aggression
        W2 = W2 - J_W2(x, y) * aggression
        W3 = W3 - J_W3(x, y) * aggression
        b1 = b1 - J_b1(x, y) * aggression
        b2 = b2 - J_b2(x, y) * aggression
        b3 = b3 - J_b3(x, y) * aggression

        if (iterations%100==0) :
            nf = network_function(x)[-1]
            ax.plot(nf[0],nf[1], lw=2, color=magentaTrans);
        iterations -= 1

    nf = network_function(x)[-1]
    ax.plot(nf[0],nf[1], lw=2.5, color=orange);


def training_data (N = 100) :
    x = np.arange(0,1,1/N)
    y = np.array([
      16*np.sin(2*np.pi*x)**3,
      13*np.cos(2*np.pi*x) - 5*np.cos(2*2*np.pi*x) - 2*np.cos(3*2*np.pi*x)- np.cos(4*2*np.pi*x)
    ]
    ) / 20
    y = (y+1)/2
    x = np.reshape(x, (1, N))
    #y = np.reshape(y, (2, N))
    return x, y

def make_colormap(seq):
    seq = [(None,) * 3, 0.0] + list(seq) + [1.0, (None,) * 3]
    cdict = {'red': [], 'green': [], 'blue': []}
    for i, item in enumerate(seq):
        if isinstance(item, float):
            r1, g1, b1 = seq[i - 1]
            r2, g2, b2 = seq[i + 1]
            cdict['red'].append([item, r1, r2])
            cdict['green'].append([item, g1, g2])
            cdict['blue'].append([item, b1, b2])
    return mcolors.LinearSegmentedColormap('CustomMap', cdict)

magenta = (0xfc/255, 0x75/255, 0xdb/255) # Brighter magenta
magentaTrans = (0xfc/255, 0x75/255, 0xdb/255, 0.1) # Brighter Transparent magenta
orange = (218/255, 171/255, 115/255)
green = (175/255, 219/255, 133/255)
white = (240/255, 245/255, 250/255)
blue1 = (70/255, 101/255, 137/255)
blue2 = (122/255, 174/255, 215/255)

blueMap = make_colormap([blue2, blue1])

앞에서 선언한 jacobian 함수들과 plot_training 그리고 training_data을 이용해서 Neural Network 학습을 해볼 수 있습니다.

x, y = training_data()
reset_network()

plot_training(x, y, iterations=10000, aggression=7, noise=1)

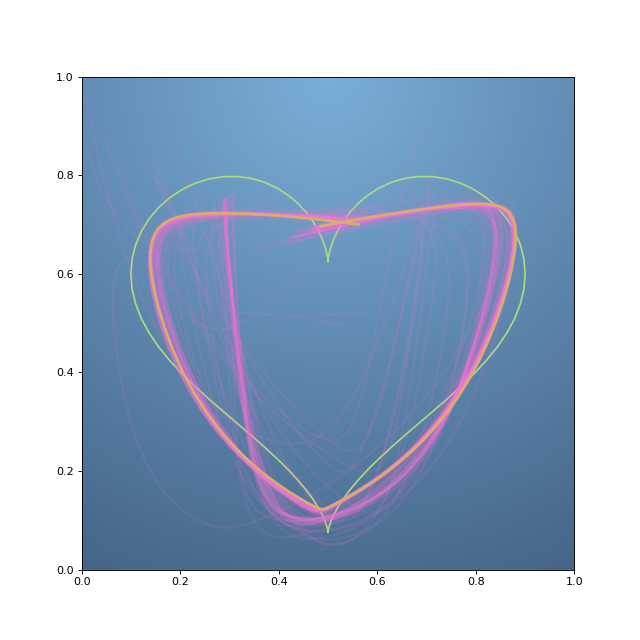
$Drawing$

위 코드 중 이 부분이 학습의 핵심 입니다. 아래의 while 문을 한번 보시기 바랍니다.
partial derivative를 이용하여 계산한 값을 빼주어서 weight와 bias를 업데이트 합니다. 앞에서 다룬 내용 그대로 입니다.
여기서 사용된 aggression은 얼만큼의 가중치로 변화율을 반영해 줄 것인지에 대한 하이퍼 파라미터로 소위 말하는 learning rate입니다.

while iterations>=0 :
    W1 = W1 - J_W1(x, y) * aggression
    W2 = W2 - J_W2(x, y) * aggression
    W3 = W3 - J_W3(x, y) * aggression
    b1 = b1 - J_b1(x, y) * aggression
    b2 = b2 - J_b2(x, y) * aggression
    b3 = b3 - J_b3(x, y) * aggression

여기 까지 이번 글에서는 multivariate chain rule에 대하여 다루어 보았고 그 개념을 통해 neural network를 간략하게 만들어 보았습니다.

mathematics for machine learning 글 목록

목차

multivariate chain rule

neural network

training neural network

backpropagation practice

multivariate chain rule

neural network

training neural network

backpropagation practice