산술, 기하, 조화 평균
2020, Sep 19
- 참조 : https://towardsdatascience.com/on-average-youre-using-the-wrong-average-geometric-harmonic-means-in-data-analysis-2a703e21ea0
- 참조 : http://groups.di.unipi.it/~bozzo/The%20Harmonic%20Mean.htm
- 이번 글에서는 산술, 기하, 조화 평균의 의미를 살펴보고 어떤 상황에서 각 평균을 사용할 수 있는 지 알아보도록 하겠습니다.
목차
산술 평균 (arithmetic mean)
- 먼저 가장 간단한
산술 평균 (arithmetic mean)은 단순히 모든 수를 더한 다음에 더한 수의 갯수 만큼 나누는 과정입니다. - 산술 평균이 잘 작용하려면 평균을 구하려는 데이터 셋의 분포가 선형적이어야 합니다.
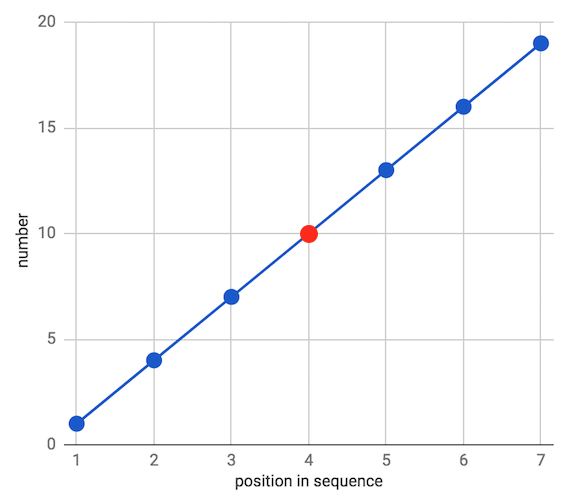
- 위 그림의 산술 평균 과정은 다음과 같습니다.
- \[(1 + 4 + 7 + 10 + 13 + 16 + 19) ÷ 7 = 10\]
- 위 데이터셋은 선형적이기 떄문에 산술 평균인 10이 평균을 잘 표현합니다.
- 따라서 산술 평균은 선형적 또는 등차 관계에 가까운 데이터 셋에서 잘 작동합니다.
기하 평균 (geometric mean)
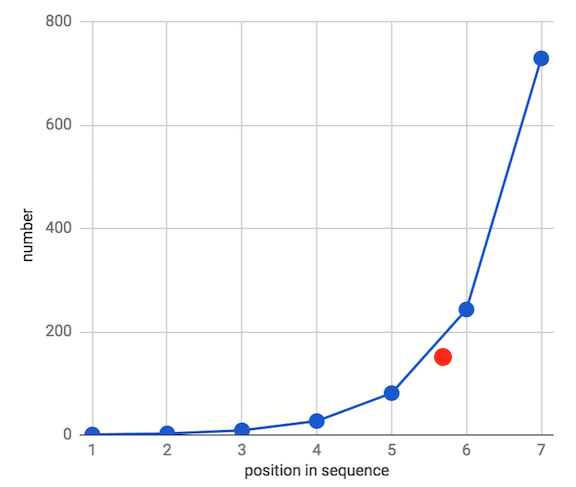
- \[1 + 3 + 9 + 27 + 81 + 243 + 729) ÷ 7 = 156.1\]
- 하지만 위 그림과 같이 비선형적인 데이터 셋에서는 산술 평균은 전체의 중앙값을 나타내진 않습니다.
- 하지만 위 데이터의 관계는 등비 관계입니다. 즉, 데이터 간 곱의 관계가 있다고 할 때 사용하는 평균이
기하 평균(geometric mean)입니다. - 기하 평균은 데이터를 모두 곱한 다음에 데이터의 갯수만큼의 sqaure를 취해주는 방식입니다.
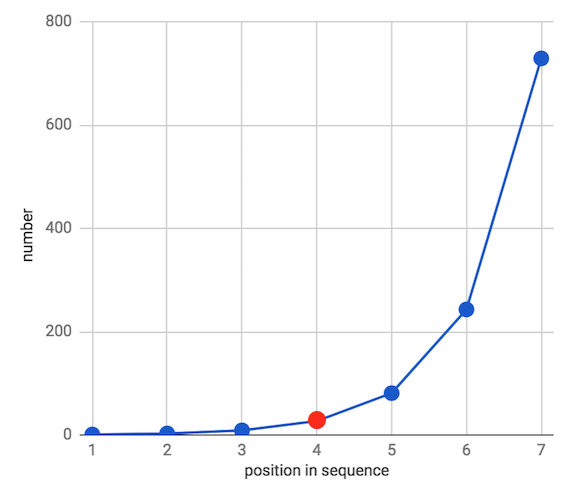
- \[(1 * 3 * 9 * 27 * 81 * 243 * 729)^{1/7} = (10,460,353,203)^{1/7} = 27\]
- 따라서 데이터의 관계가 합의 관계 또는 선형 관계가 아니라 곱의 관계라면 기하 평균을 사용하면 됩니다.
- 기하 평균을 사용하는 또 다른 예는 데이터의 스케일이 다른 경우 입니다.
- 예를 들어 어떤 가게의 평점이 5점 만점으로 매긴 점수와 100점 만점으로 매긴 점수가 있다고 가정하겠습니다.
- 가게1은 5점 만점 중 4.5점과 100점 만점 중 68점을 받았고 가게 B는 3점과 75점을 받았다고 하겠습니다. 평균은 어디가 높을 까요?
- 단순히 산술 평균을 하면
가게1 = (4.5 + 68) / 2 = 36.25,가게2 = (3 + 75) / 2 = 39점을 받았으므로 가게 2가 더 평균이 큽니다. - 하지만 실제 스케일이 다른 두 값의 평균을 계산할 때, 단술 산술 평균을 매기진 않습니다. 정규화 과정을 통하여 범위를 통일 시킵니다. 위 예시의 경우 5점 기준의 점수에 20을 곱하면 100점 기준 점수로 범위를 맞출 수 있고 그 뒤에 산술 평균을 적용하면 평균을 낼 수 있습니다.
가게1 = ((4.5 * 20) + 68) / 2 = 79,가게2 = ((3 * 20) + 75) / 2 = 67.5로 계산하여 가게1의 평균이 더 커졌습니다. 그리고 이 방법이 더 합리적입니다. 그런데 이 과정은기하 평균의 과정과 같습니다.가게1 = squre root of (4.5 * 68) = 17.5,가게2 = square root of (3 * 75) = 15가 됩니다. 기하 평균의 경우에도 가게1의 평균값이 더 높게 나옵니다.- 이와 같은 이유는 산술평균의 경우 큰 스케일에 더 큰 가중치를 두기 때문에 왜곡이 발생하여 큰 스케일에 더 큰 가중치를 둔 평균을 계산하는 반면 기하평균의 경우 합이 아니라 곱을 하기 때문에 서로의 값에 스케일이 반영되므로 왜곡이 발생하지 않습니다.
- 또한 기하 평균에서는 데이터 셋에 0이 있으면 안됩니다. 0을 곱하는 순간 0이 되기 때문에 0은 제외하고 계산을 해야합니다.
조화 평균 (harmonic mean)
- 산술 평균이 합과 관련된 데이터, 기하 평균이 곱과 관련된 데이터와 관련있다면 조화 평균은
역수와 관련된 데이터와 관련 있습니다. - 조화 평균을 위한 절차는 다음과 같습니다.
- ① 데이터셋의 모든 수의 역수를 취합니다.
- ② 역수를 취한 수들의 산술 평균을 구합니다.
- ③ 산술 평균을 다시 역수를 취합니다.
- \[H = \frac{n}{\frac{1}{x_{1}} + \frac{1}{x_{2}} + \cdots + \frac{1}{x_{n}}} = \frac{1}{\sum_{i=1}^{n}\frac{1}{x_{n}}} = \Biggl(\frac{\sum_{i=1}^{n}\frac{1}{x_{n}}}{n} \Biggr)^{-1}\]
- 예를 들면 다음과 같습니다.
- \[\frac{1^{-1} + 4^{-1} + 4^{-1}}{3} = \frac{3}{\frac{1}{1} + \frac{1}{4} + \frac{1}{4}} = \frac{3}{1.5} = 2\]
- 조화 평균 또한 기하 평균과 마찬가지로 데이터 셋에 0이 있으면 계산이 불가합니다. 따라서 0에 대한 처리를 해주어야합니다.
- 그러면 위와 같이 역수의 산술평균을 구하는 방식은 어떤 상황에서 사용할 수 있을까요?
- 각 데이터가 의미하는 길이나 데이터가 측정된 시간등의 비율이 다를 떄 조화 평균을 사용할 수 있습니다. 조화 평균에 가장 많이 사용되는 평균 속도 문제로 이해해 보도록 하겠습니다.
- 출발 지점에서 도착 지점까지 5km가 되는 거리를 이동하는 데 30kph로 이동하고 도착지점에서 출발 지점까지 다시 오는데 10kph로 이동한다고 가정해 보겠습니다. 이 때, 사용한 도로는 같기 때문에 같은 거리를 이동하였습니다.
- 전체 이동하는 동안의 평균 속도를 구할 떄 단순히 산술 평균으로 (10 + 30) / 2 = 20 kph로 구하면 안된다는 것을 중고등학교 떄 배웠습니다.
- 왜냐하면 같은 거리를 이동하였으므로 30 kph로 이동하였을 떄, 훨씬 짧은 시간 동안 이동하였고 반면 10kph로 이동한 시간이 길기 때문에 전체 평균 속도는 10kph에 가까워져야 하기 때문입니다.
- 따라서 정확한 산술 평균을 구하기 위해서는 이동한 시간만큼의 가중치를 반영해 주어야 합니다.
- 5km거리를 30kph로 이동하였으면 10분 동안 이동하였고 10kph로 이동하였으면 30분 동안 이동하였습니다. 따라서 총 이동 시간은 40 분입니다.
- 따라서 가중치를 적용한 산술 평균은 (30kph * (1/4)) + (10kph * (3/4)) = 15 kph가 됩니다. 따라서 가중치가 없을 때 보다 평균이 줄어든 것을 확인할 수 있습니다.
- 이를 조화 평균 식을 이용하여 적용해 보도록 하겠습니다.
- \[(\frac{2}{\frac{1}{30} + \frac{1}{10}})^{-1} = (\frac{1}{15})^{-1} = 15\]
- 이와 같이 조화 평균을 사용하는 경우는
가중치가 있는 산술 평균에서 사용할 수 있습니다.
- 지금 까지 내용 중 어떤 경우에 산술, 기하, 조화 평균을 사용할 수 있는지 정리해 보도록 하겠습니다.
기하 평균:- ① 데이터셋의 스케일이 다른 경우 사용할 수 있음.
- ② 데이터가 곱의 관계를 가지고 있는 경우.
- ③ 평균이 중앙값에 가깝도록 만들고 싶은 경우
- ④ 불균형한 데이터 셋에 페널티를 주고 싶은 경우
조화 평균:- ① 데이터가 측정된 기간이 다른 경우 사용할 수 있음.
- ② 가중치가 있는 산술 평균에 사용할 수 있음.
- ③ 평균이 작은 값에 가깝도록 만들고 싶은 경우
- ④ 불균형한 데이터 셋에 큰 페널티를 주고 싶은 경우
산술 평균:- 기하 평균, 조화 평균 사용이 필요없을 떄 또는 사용할 수 없을 때 사용할 수 있음.
- 데이터의 관계가 합의 관계일 때 사용할 수 있음.
- 평균이 큰 값에 가깝도록 만들고 싶은 경우
산술 기하 조화 평균의 관계
- 이번에는 산술 기하 조화 평균들의 관계에 대하여 알아보도록 하겠습니다.
- 먼저 같은 데이터 셋을 이용하여 산술, 기하, 조화 평균을 구하면 다음과 같은 관계를 가집니다.
- \[\text{harmonic mean} \le \text{geometric mean} \le \text{arithmetic mean}\]
- 위 관계는 직접 식을 전개해서 비교해 보면 쉽게 증명할 수 있습니다. 등호가 성립하는 경우는 데이터가 모두 같을 떄 입니다.
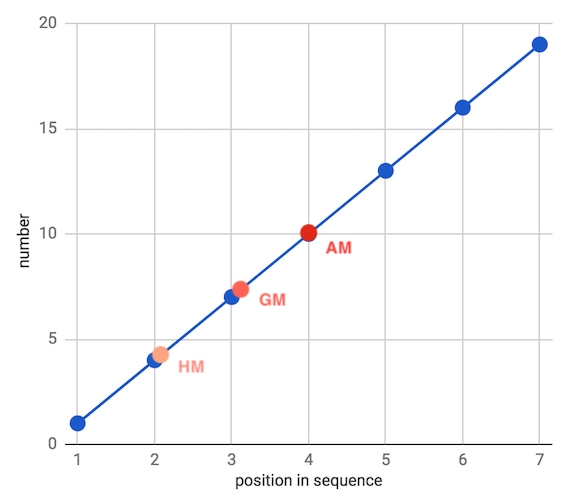
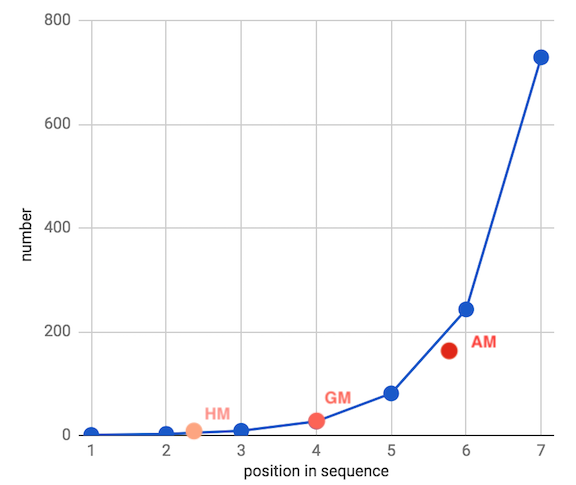
- 따라서 위 그래프와 같이 항상
조화 < 기하 < 산술평균 순서의 크기로 나타나며 이 성질에 따라서 조화 평균은 데이터셋에서 작은 값들에 좀 더 가깝게 평균이 나오고 기하 평균은 중앙값들에 산술 평균은 큰값들에 좀더 반영되어 평균값들이 도출됩니다.
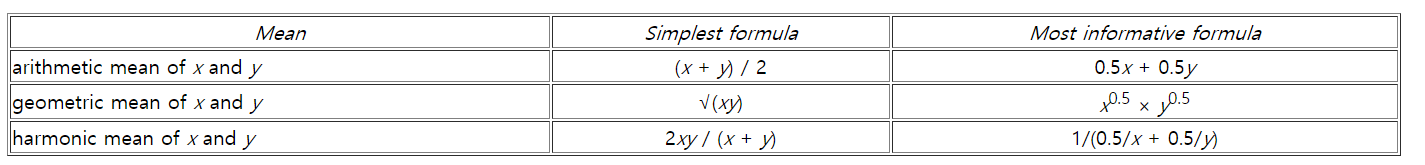
- 위 테이블에 따라서 아래 예제를 구해보겠습니다.

- 위 테이블을 보면 산술 평균의 경우 모든 평균이 50인 반면 기하 평균과 조화 평균은 불균형한 데이터 셋의 경우 좀 더 낮은 평균을 가집니다. 특히
조화 평균의 경우 불균형한 데이터 셋에 큰 페널티가 가해집니다. - 예를 들어 X 과목과 Y 과목의 평균을 계산할 때, 두 과목의 점수 차가 큰 경우 페널티를 주고 싶다면 조화 평균을 사용하여 페널티를 줄 수 있습니다. 이 경우 불균형한 데이터 일수록 평균이 낮아집니다.
피타고라스 평균
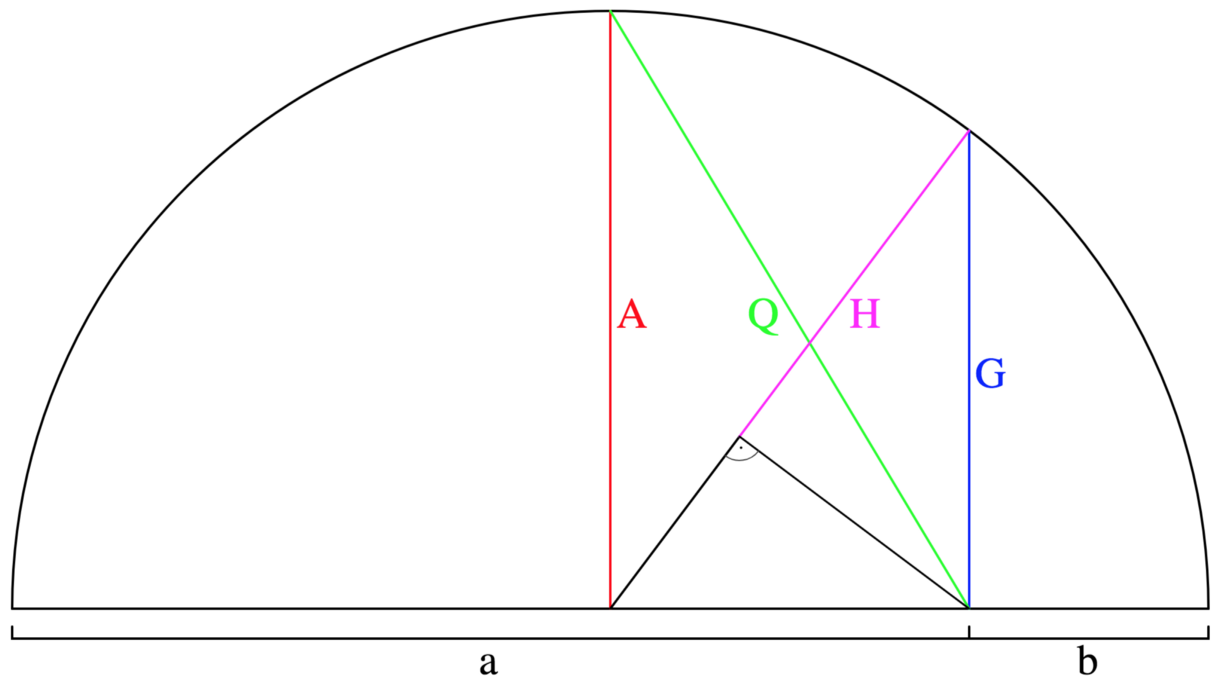
- 피타고라스 평균은 앞에서 배웠던 산술, 기하, 조화 평균을 나타냅니다. 특히, 피타고라스 평균은 위 그림을 통하여 한번에 나타낼 수 있습니다. 산술 평균 (A), 기하 평균 (G), RMS(Root Mean Square) (Q) 그리고 조화 평균 (H)를 유도해 보겠습니다.
- \[A = \frac{a + b}{2}\]
- 원의 반지름이 산술 평균과 같으므로 기하 평균은 피타고라스 정리를 통해 다음과 같이 구할 수 있습니다.
- \[(A - b)^{2} + G^{2} = A^{2}\]
- \[A^{2} -2Ab + b^{2} + G^{2} = A^{2}\]
- \[G^{2} = 2Ab - b^{2} = (a + b)b - b^{2} = ab\]
- \[G = \sqrt{ab}\]
- Q는 RMS로 식으로 표현하면 \(\sqrt{(a^{2} + b^{2})/2}\) 입니다. 이 또한 피타고라스 정리를 통해 구할 수 있습니다.
- \[Q^{2} = A^{2} + (A-b)^{2} = A^{2} + A^{2} -2Ab + b^{2} = 2A^{2} -2Ab + b^{2} = \frac{(a + b)^{2}}{2} - (a+b)b + b^{2} = \frac{a^{2} + b^{2}}{2}\]
- \[Q = \sqrt{\frac{1}{2}(a^{2} + b^{2})}\]
- 마지막으로 위 그림을 보면 조화 평균 H의 길이는 정확하게 나타낼 수 없지만 대소 관계를 나타낼 수 있습니다. H를 높이 G를 빗변으로 하는 직각삼각형을 보면 H는 G보다 항상 작거나 같아야 합니다.
- \[H = \frac{1}{\frac{1}{2}(\frac{1}{a} + \frac{1}{b})} = \frac{2ab}{a + b} = G \cdot \frac{G}{A}\]
- 위 관계에서 항상 \(A \ge G\)이기 때문에 \(0 \lt \frac{G}{A} \le 1\)의 관계를 가지므로 \(H \le G\) 관계를 가지게 됩니다.
- 이상으로 도형에서의 산술, 기하, 조화 평균을 알아보았습니다.