(베이즈 통계학 기초) 1. 정보를 얻으면 확률이 바뀐다.

2019, Mar 03    

통계학 관련 글 목록

• 출처 : 세상에서 가장 쉬운 베이즈 통계학 입문
• 베이즈 이론에 대하여 간략하게 알아보기 위하여 손님이 쇼핑족인지 아이쇼핑족인지 분류하는 예제를 다루어 보도록 하겠습니다.

1. 경험에서 사전확률을 설정합니다.

• 추측을 위해 가장 먼저 해야 할 일은 손님의 두 가지 타입 - 쇼핑족과 아이쇼핑족에 대해 그 비율이 각각 몇인지 수치로 배정하는 것입니다.
  • 이러한 타입을 클래스 라고도 하며 이런 타입의 확률(비율)을 사전확률이라고 합니다.
  • 사전이란 어떤 정보가 들어오기 전을 뜻하는 말이고 이때 정보란 손님이 말을 거는 행동을 했다 와 같은 추가적인 상황을 뜻합니다.
• 추가적인 상황을 통하여 타입에 대한 추측을 업데이트 하게 되는데, 사전확률이라고 하면 추가정인 정보 즉, 관측이 이루어지기 전의 상태 입니다.

• 만약 경험에 의하여 쇼핑족의 비율이 20% 즉, 0.2임을 알고 있다고 가정해 보겠습니다. 그러면 아이쇼핑족은 0.8이 됩니다. 이 비율이 사전확률에 해당하고 타입에 대한 사전분포 라고 합니다.

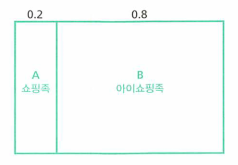
• 큰 직사각형을 2개의 직사각형으로 분할하는데, 면적의 비율이 각각 0.2와 0.8이 되도록 분할합니다. 면적은 베이즈 확률을 다루는 데 중요한 역할을 합니다.
• 여기서 면적을 0.1과 0.4 또는 1과 4등으로 쓰지 않고 0.2와 0.8로 사용한 이유는 확률은 전부 더해서 1이 되도록 설정한다는 성질 때문입니다. 이것을 정규화 조건이라고 합니다.

2. 타입별로 말을 거는 행동을 하는 조건부 확률을 설정합니다.

• 다음 단계로 쇼핑족에 속하는 손님과 아이쇼핑족에 속하는 손님이 각기 어느 정도의 확률로 점원에게 말거기 행동을 하는가를 설정해야 합니다.
  • 이 때 확률은 어떠한 경험, 실증, 실험에 기반한 수치가 필요합니다.

• 위 행동에 대한 조건부 확률은 계산이 간단해지도록 임의로 설정하였습니다.
• 여기서 주의할 점은 표를 가로 방향으로 보면 정규화 조건이 충족됩니다.
  • 가로 방향은 특정 타입 즉, 클래스에 따라서 분류한 것으로 각 클래스별 발생 확률의 총합은 1이 됩니다.
• 반면 세로 방향으로 보면 정규화 조건이 충족되지 않습니다.
  • 각기 다른 타입의 사람에 대한 행동을 나타내고 있는 것으로 행동 전체를 아우르는 확률적 사건이 아니므로 더해도 1이 안됩니다.
• 이 표는 조건부 확률을 나타냅니다. 즉, 타입을 한정한 경우 각 행동의 확률에 해당합니다.
• 만약 타입을 행동의 원인으로 본다면 원인을 알고 있을 때의 결과의 확률이라고 해석할 수 있습니다.

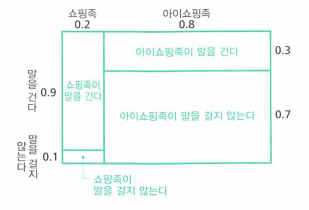
• 두가지 타입(쇼핑족과 아이쇼핑족)과 행동(말을 건다, 안건다)를 가지고 4가지 경우로 분리를 하면 위 표와 같습니다.
• 각 구역에 나타나는 사항의 확률이 각 직사각형의 면적과 같습니다.

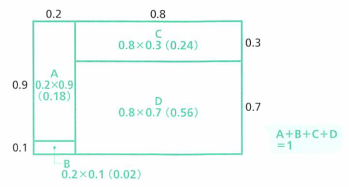
• 면적을 구하는 방법은 위와 같고 면적의 총합은 1이 됩니다.

3. 관측한 행동에서 가능성이 사라진 세계를 제거합니다.

• 만약 손님이 말을 걸었다고 하면 손님의 행동을 한 가지 관측한 것입니다. 즉, 추가적인 정보를 얻은 것입니다.
• 이 경우 말을 걸지 않는다 라는 관측은 사라지게 됩니다. 즉, 전체 공간이 한정되었음을 의미합니다. 이것을 도형에서 반영해 보겠습니다.

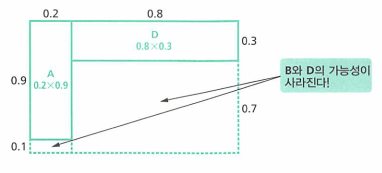
• 가능한 영역이 4개에서 2개로 줄어들었고 새로운 추측값을 얻을 수 있게 됩니다.
• 가능성의 일부가 사라지고 나머지 일부로 현실이 한정된다면 확률의 변화가 생깁니다.

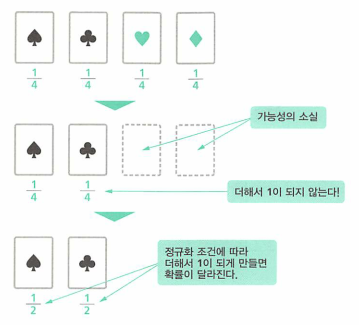
• 예를 들어 52장의 트럼프를 잘 섞어서 뒤집어 놓고 맨 위의 카드는 무슨 모양일까? 라고 물어보겠습니다.
• 스페이드 라고 답을 하면 확률은 1/4 입니다. 왜냐하면 네가지 모양이 모두 대등하게 나올 수 있기 때문입니다.
• 만약 상대가 맨 위의 카드는 검정색 무늬입니다. 라고 가르쳐준다면 빨간색의 가능성은 사라집니다. 따라서 추측도 달라지게 됩니다.
  • 이 때, 스페이드가 맞을 확률은 1/2가 됩니다.
• 맨 처음 네 가지 무늬의 확률을 더했을 때 1입니다. 그러나 빨간 무늬일 가능성이 사라짐으로써 스페이드일 확률과 클러보일 확률의 합은 1이 되지않습니다.
• 비례관계를 유지한 채 정규화 조건을 적용하여 스페이드일 확률은 1/2로 바뀌게 됩니다.

4. 쇼핑족의 베이즈 역확률을 구한다.

• 앞에서 말을 건다는 행동을 관측하였기에 가능 케이스는 두 개로 한정되었습니다.
  • 쇼핑족 & 말걸기
  • 아이쇼핑족 & 말걸기

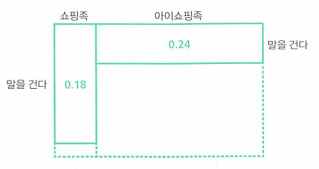
• 행동의 관측에 따라 가능성이 두 가지로 좁혀졌기 때문에 각각의 확률을 더해도 1이 되지 않습니다.
• 비례 관계를 유지한 채 정규화 조건을 적용시켜보겠습니다.
  • 왼쪽 직사각형의 면적 : 오른쪽 직사각형의 면적 = 0.18 : 0.24 = 3 : 4
  • 왼쪽 직사각형의 면적 : 오른쪽 직사각형의 면적 = 3 : 4 = \(\frac{3}{7} : \frac{4}{7}\)

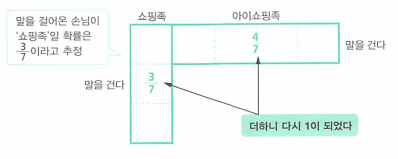
• 이 표에서 말을 걸어온 손님이 쇼핑족일 확률은 3/7 이라고 추정할 수 있습니다.
  • 이 확률을 베이즈 역확률 또는 사후확률 이라고 합니다.
• 앞에서는 손님의 타입이 두 종료이며 각기 타입이 1)말을 건다, 2)말을 걸지 않는다 였습니다.
  • 타입은 원인 그리고 행동은 결과로 바라보고
  • 타입이라는 원인으로 부터 행동이라는 결과가 일어난다고 파악하였습니다.
• 위 표에서는 말을 건 사람이 쇼핑족과 아이쇼핑족의 타입 중 하나의 타입을 확률적으로 선택하고 있습니다.
  • 말을 건다 라는 행동의 결과로부터 타입이라는 원인으로 거슬러 올라갑니다.
  • 결과 → 원인이 바로 역확률 입니다.

베이즈 추정의 프로세스 정리

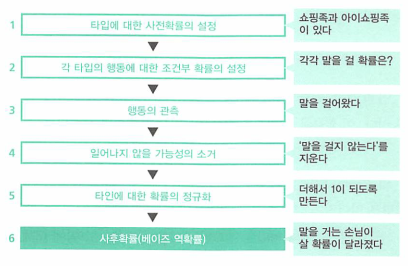
• 사후확률을 통해 과연 무엇을 알 수 있을까요?

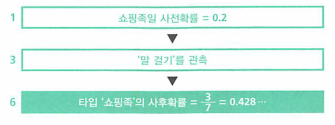
• 사전확률 관점에서 보면 쇼핑족일 확률은 0.2였지만 행동을 관측한 후(말 걸기) 확률이 변경되었습니다.(사후확률) 이것을 베이즈 업데이트 라고 합니다.
• 베이즈 추정의 정의는 사전확률을 행동의 관찰(정보)에 의거해 사후확률로 베이즈 업데이트 하는 것입니다.

통계학 관련 글 목록