(베이즈 통계학 기초) 베이지안 추정은 때로 직감에 크게 반한다.(1)

2019, Mar 03    

• 출처 : 세상에서 가장 쉬운 베이즈 통계학 입문

암에 걸려있을 확률을 계산

• 다루어 볼 문제는 검사에 따라 얻은 X가 병인지 아닌지 판단하는 내용입니다.
• 만약 특정 암에 걸려 있다면 95% 확률로 양성이 나오는 검사를 받은 결과 양성 판정이 나왔다고 가정해 봅시다.
  • 이 때 그 암에 걸려 있을 확률이 95% 일까요?
  • 정답은 아니오입니다.
• 양성이라는 결과로부터 당신이 암일 확률을 추정해 보면 수치가 높지 않습니다.
  • 베이즈 추정은 결과(관측) -> 원인(타입)으로 역추적 하는 과정입니다.

문제

• 어느 특정 암에 걸릴 확률을 0.1%(0.001)이라고 하자. 이 암에 걸렸는지를 진단하는 간이검사가 있는데, 이 암에 걸려 있는 사름은 95%(0.95)의 확률로 양성 진단을 받는다고 하겠습니다.
• 한편 건강한 사람이 양성으로 오진을 받을 확률은 2%(0.02)이니다.
• 그렇다면 이 검사에서 양성이라고 진단받았을 때, 당신이 암에 걸려있을 확률은 얼마나 될까요?
  • 즉, \(p(암 \vert 양성)\)일 확률은?

의료데이터를 근거로 사전확률을 설정합니다.

• 추정의 과정은 앞의 글의 방법과 같습니다.
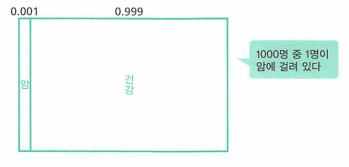
• 사전 확률 : 각 타입에 대한 정보를 얻기 전의 존재 확률
  • 위 문제에서 타입은 2가지 입니다.
    • 암에 걸려있는 사람
      • 0.001
    • 건강한 사람
      • 0.999

• 암이 걸릴 확률에 따른 사전분포는 위와 같습니다.
• 이 확률은 사전 확률로 간이 검사를 받기 전에 암인가 아닌가의 가능성입니다.
• 나의 몸상태를 잘 모른다면 두 가지 타입 중 한 타입을 선택 할 때 개인적인 정보가 없으므로 현재로서는 암일 확률이 0.001 건강할 확률이 0.999라고 추측할 수 있습니다.

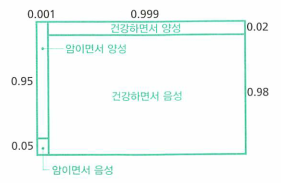
검사의 정밀도를 근거로 조건부 확률을 설정합니다.

• 타입별로 특정한 정보를 초래하는 조건부 확률을 설정해야 합니다.
• 검사 결과로서의 양성, 음성이 바로 정보에 해당됩니다.

• 이 표에서 확인할 수 있는 것은 검사가 완벽하지 않으며 오진의 위험이 있다는 것입니다.
  • 암에걸린환자를 음성으로 판단할 확률
  • 건강한 사람을 양성이라고 판단할 확률
• 위 확률은 타입을 한정한 경우에 각 검사 결과의 조건부 확률 입니다.
• 타입을 검사 결과의 원인으로 잡는다면, 원인(암 또는 건강)을 알고 있을 때의 결과(양성 또는 음성)의 확률 이라고 볼 수 있습니다.

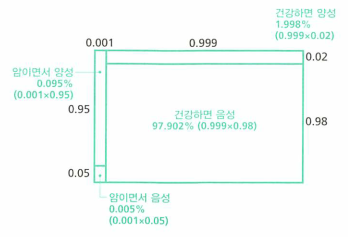
• 두개의 타입과 두개의 관측에서 나타날 수 있는 모든 경우의 수는 위와 같습니다.

• 각 영역의 면적은 확률의 곱으로 나타낼 수 있습니다.

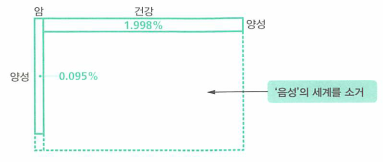
검사 결과가 양성이므로 일어날 가능성이 없는 영역을 소거 합니다.

• 만약 양성 판정을 받았다고 가정합시다.
  • 즉, 추가적인 정보를 얻게 된 것입니다.

• 양성 이라는 진단을 관측했기 때문에 음성이라는 관측은 배제됩니다.

암일 것이라는 베이즈 역확률을 구합니다.

• 앞에서 양성이라는 진단을 관측했기 때문에 가능한 케이스가 두개로 한정됩니다.
  • 암 & 양성
  • 건강 & 양성
• 검사 결과가 관측됨에 따라 가능성이 네 개에서 두 개로 좁혀졌기 때문에 확률인 직사각형의 면적을 더해도 1이 안됩니다.
• 따라서 정규화 조건을 복구 하기 위하여 더해서 1이 되도록 만듭니다.

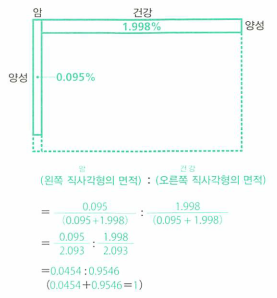
• 왼쪽 직사각형의 면적 : 오른쪽 직사각형의 면적 = 0.095 : 1.998
  • 0.095 + 1.998 = 2.093이 정규화를 위한 상수가 됩니다.
• 계산을 하면 \(P(암 \vert 양성) = 0.0454\) 임을 알 수 있습니다.
  • 이 값이 사후확률이 됩니다.

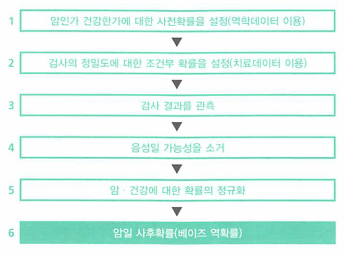
베이즈 추정의 프로세스 정리

• 암에 걸려 있을 사후 확률을 구하는 것은 어떤 의미가 있을까요?
• 처음에 한 질문이 95% 정확도인 암 검사에서 양성이 나온다면 95% 확률로 암인가? 에 대한 질문은 아니오가 답이었습니다.
  • 앞에서 보았듯이 불과 4.5% 입니다.
• 즉, 원래 암에 걸린 사람 자체가 매우 드뭅니다. 건강한 사람이 압도적으로 많을 뿐더러 건강한 사람을 양성으로 진단하는 사례 또한 무시할 수 없을 만큼 많기 때문입니다.
• 하지만 중요한 의의는 다음과 같습니다.

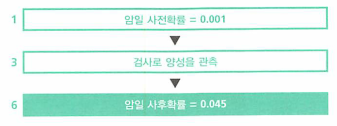
• 이 도식을 보면 사전확률로 암일 확률은 0.001 이었지만 관측 후 양성일 때 암일 확률은 0.045로 45배가 증가하였습니다.
• 사전 확률로 봤을 때에는 1000명당 1명이 암이라고 생각했지만, 관측 후 양성이면 20명당 1명의 꼴로 암이라고 판단되는 상태가 됩니다.