(베이즈 통계학 기초) 주관적인 숫자여도 추정이 가능하다.

• 출처 : 세상에서 가장 쉬운 베이즈 통계학 입문

베이즈 추정은 이유가 불충분한 상황에서도 사용할 수 있습니다.

앞에 글에서 살펴본 바로는 베이즈 추정은 다음과 같은 절차를 통해 추정을 하게 됩니다.

• 사전 확률 -> 조건부 확률 -> 관측에 의한 정보의 입수 -> 사후 확률

1. 주관적인 데이터 사용

• 앞의 글에서 다루었던 예제1과 예제2에서는 객관적인 데이터를 사용하였었습니다.
• 반면 이번 글에서 다루어 볼 내용은 객관적인 사전 데이터가 없어도 추정이 가능하다는 것을 베이즈 추정을 통해 알아보려고 합니다.
  • 사전확률을 주관적으로 설정하여 추정을 실시할 수 있습니다.

당신이 남자라고 가정하자. 특정 여성 동료가 자신에게 호감을 가지고 있는지 알고 싶은 상황입니다. 그런 와중에 당신은 발렌타인데이에 그녀로부터 초콜릿을 받았습니다. 이 때 그녀가 당신을 진지하게 생각하고 있을 확률이 얼마라고 추정해야 할까요?

이 문제에서는 두가지 큰 어려움이 있습니다.

• 첫째, 사람의 속마음을 수치화 해야한다는 것입니다.
• 둘째, 이 문제에서 말하는 확률을 정확하게 정의하기 어렵습니다.
  • 주사위 처럼 시행을 해서 횟수를 셀 수도 없습니다.
• 하지만, 베이즈 추정은 이러한 문제에서도 적용할 수 있습니다.

2. 주관적으로 당신을 마음에 두고 있는가에 대한 사전확률을 설정합니다.

• 위에서 정의한 문제의 특수성은 사전확률을 객관적인 통계 데이터를 이용할 수 없다는 점입니다.
  • 사전확률 이란 어떤 정보가 들어오기 전 각 타입에 대한 비율을 뜻합니다.
• 위 문제에서 사전 확률을 정의한다면 진심(당신을 마음에 두고 있다)과 논외(당신을 논외로 생각중)로 타입을 나눌 수 있습니다.
  • 앞에서 언급한 바와 같이 이러한 문제는 통계적 데이터가 없으므로 사전확률을 구하기 위해 활용 가능한 데이터가 없습니다.
• 이와 같은 경우는 이유 불충분의 원리라는 방법을 이용하는 것이 좋습니다.
  • 일단 두 타입이 대등하다고 판단하는 원리입니다.
    • 여자 동료가 나를 진심으로 대하는 것도, 논외로 생각하는 것도 어떤 근거가 없습니다.
    • 따라서 진심 : 논외 = 0.5 : 0.5로 생각할 수 있습니다.

• 위 그림은 이유 불충분의 원리에 따른 사전 분포에 해당합니다.
  • 즉 타입에 대한 사전 분포가 없는 상태에서는 1/n 으로 확률을 만들 수 있습니다.
  • 전혀 사전 정보가 없으므로 대등하기 할당하는 방법입니다. 물론 다르게 수치를 할당할 수도 있습니다.

3. 어떻게든 데이터를 입수하여 조건부 확률을 설정합니다.

• 다음 단계에서는 관측할 수 있는 행동에 대해서 타입별로 조건부 확률을 설정해야 합니다.
• 이 조건부 확률에 대해서는 어느 정도의 객관적인 확률을 설정할 필요가 있습니다.
  • 즉, 어딘가에서 통계적인 데이터를 꼭 끌고와야 합니다.
• 이런 경우에 설문 조사 같은 것이 좋은 방법이 될 수 있습니다.
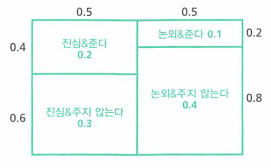
• 예를들어 진심과 논외 타입에 대하여 초콜릿을 주는가를 조사를 하였을 때,
  • 진심으로 좋아하는 사람에게는 42.5% 확률로 초콜릿을 줍니다.
  • 논외인 사람에게는 22% 확률로 초콜릿을 줍니다.
  • (필자가 직접 조사해본 데이터 라고 합니다.)
• 통계적인 데이터(설문조사)한 내용을 정리해보면 다음과 같습니다.

• 원인(진심 및 논외)을 알고 있을 때의 결과(준다/주지 않는다.)의 확률 입니다.
  • 즉, likelihood가 됩니다.

• 타입(진심/논외) 관측(준다/주지 않는다)를 이용하여 4개의 영역으로 분할하면 위와 같습니다.

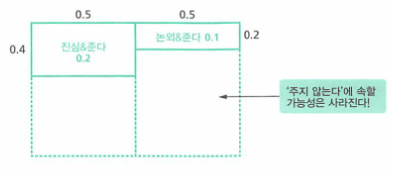
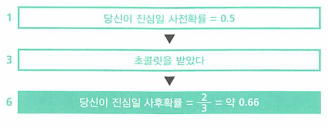
4. 초콜릿을 받았으므로 일어날 가능성이 없는 영역을 제거합니다.

• 초콜릿을 받았다고 관측되었다면 주지 않는다는 영역은 제거합니다.

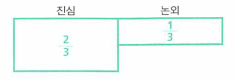
• 전체 확률을 1로 만들기 위하여 정규화 조건을 적용시켜 줍니다.
• 따라서 어떤 여자로부터 초콜릿을 받았다면 진심일 확률은 2/3가 된다고 추정할 수 있습니다.

• 사전 확률에 대한 정보가 전혀 없다면 이유 불충분 원리를 이용하여 uniform 하게 확률을 나눌 수 있습니다.
• 하지만 likelihood에 관한 조건부 확률은 반드시 통계적으로 데이터를 이용한 접근이 필요합니다.

• 초콜릿을 받기 전에는 5:5 라고 생각했던 상대방의 마음을 사전 조사를 이용하여 접근한 결과 50% -> 66% 까지 상승하였습니다.
• 이 때, 5:5가 아니라 4:6, 3:7 등으로 사전 확률을 설정할 수도 있습니다.

사전확률이 없으면 이유불충분 원리로 분포를 임의적으로 정할 수 있으나, 가능도 함수는 통계적 접근이 필요합니다.