(베이즈 통계학 기초) 베이즈 추정은 "최우 원리"에 근거해 있다

2019, Mar 03    

• 출처 : 세상에서 가장 쉬운 베이즈 통계학 입문

베이즈통계학과 네이만-피어슨 통계학의 공통점

• 베이즈 통계학에서는 네이만-피어슨 통계학에서 설정하지 않는 사전확률이라는 것을 도입하였습니다.
• 사전확률은 \(P(X \vert c)\) 에서 c에 해당하며 추정하려는 것의 원인으로 여겨지는 대상을 복수로 상정하여 그것이 일어날 가능성정도로 사전확률을 설정하는 것입니다.
• 네이만-피어슨 통계학에서도 이와 같은 개념을 도입하고 있습니다.
  • 최우원리(maximum likelihood)에 대하여 알아보도록 하겠습니다.

여러 학문에서 두루 쓰이는 최우원리

• 표준 통계학과 베이즈 통계학에 공통된 발상으로 최우원리라고 불리는 사고방법이 있습니다.
• 최우원리 : 세상에 일어나는 일은 일어날 확률이 큰 사건이다.
• 현상 X와 현상 Y 중에 어느 하나를 일으키는 원인으로 A와 B의 두 가지 원인을 지목했다고 하겠습니다.
  • 원인 A : 현상 X가 현상 Y보다 압도적으로 큰 확률로 발생
  • 원인 B : 현상 Y가 현상 X보다 압도적으로 큰 확률로 발생
  • 이 때, 현상 X가 관측되었다면 원인 A와 B중 어느 쪽일까요?
• 많은 사람들이 A쪽이 원인이라고 대답할 것입니다.
• 이 논리가 최우원리입니다.

• 예를들어 다음과 같은 예제가 있을 수 있습니다.
• 누군가 물건을 잃어버렸는데, A와 B중 어느 한 사람이라고 합니다.
• A는 평소에 물건을 자주 잃어버리는 사람이고 B는 항상 잘챙기는 사람입니다.
• 누가 물건을 잃어버렸다고 생각하나요?
• A라고 대답하였다면 최우 원리는 사용한 것입니다.

베이즈 추정은 최우원리에 근거하고 있습니다.

• 앞의 글의 예제를 참조해 보겠습니다.

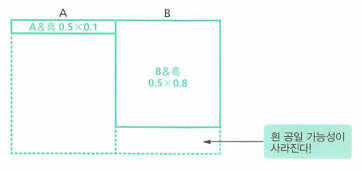
• 예제를 보면 A상자는 흰공9개, 검은공1개 / B상자는 흰공2개, 검은공8개 인 상황에서 검은공이 뽑혔다면 어떤 상자에서 뽑혔는지 예측하는 문제였습니다.
• 위 도표와 같이 검은공이 관측되었을 때, B 상자 일것이라고 판정을 내리게 되는데
  • 이 방법은 결과의 확률을 가장 높이는 원인을 선택한 결과입니다. 이것을 최우원리라고 합니다.
• 사후확률은 (사전확률) x (조건부 확률)에 비례하므로 사전확률이 크거나 조건부 확률이 큰 원인으로 선택되기가 쉽습니다.

네이만-피어슨 통계학도 최우원리에 근거하고 있습니다.

• 네이만-피어슨 통계학 또한 최우원리를 사용하고 있습니다.
  • 실제로 추정 그 자체가 아니라 통계적 추정을 입증하는 데 도입하고 있습니다.
• 통계적 추정의 입증이란 왜 그렇게 생각하는지, 그렇게 생각하는 것이 어떤 이점을 가져다 주는지 설명하는 것입니다.
• 예를 들어 하루에 한 번 일어나거나 혹은 일어나지 않는 어떤 현상이 있다고 가정해보겠습니다.
  • 손님의 총인원이 100명을 넘는 현상을 생각해 보겠습니다. 이 때 현상이 일어날 확률을 p라고 하겠습니다.
  • 이 때 일어나지 않을 확률은 1-p가 됩니다.
  • 10일을 관측한 결과 4일간 발생하였고 6일은 발생하지 않았습니다.
  • 이 때 p는 몇이라고 추정할 수 있을까요?

• 대부분이 4/10로 p를 추정하였을 것입니다. 그러면 왜 일어난 횟수의 평균치를 현상이 일어난 확률 p의 추정치로 잡는지 의심스럽지 않으신가요?
  • 몇 번 중에 몇 번 발생한 것과 발생할 확률은 직접적으로 연결이 되어 있지는 않습니다.
  • 하지만 최우원리로 인하여 이것을 입증할 수 있습니다.
• 확률 p를 이 현상이 10회중 딱 4회 일어날 확률을 L 이라고 정의해 보겠습니다.
• ·\(L = \begin{pmatrix} 10 \\ 4 \\ \end{pmatrix} p^{4}(1-p)^{6}\) 이 됩니다.
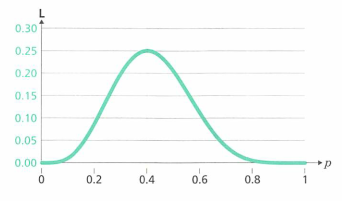
• 확률 p값을 변화시켜가면서 p와 L간의 그래프를 그려보면 다음과 같습니다.

• 그래프를 보면 p = 0.2 일때의 L값보다 p=0.4일 때의 L 값이 더 크고 이 때의 값이 가장 큰 것을 알 수 있습니다.
  • 이 때 p=0.4를 최우추정량이라고 합니다.
  • 따라서 최우추정량이 평균치가 됩니다.

• N회 관측하여 x회 일어난 경우 최우추정량이 x/N이 된다는 사실을 \(L = \begin{pmatrix} 10 \\ 4 \\ \end{pmatrix} p^{4}(1-p)^{6}\)에 미분을 사용하면 간단하게 증명할 수 있습니다.
  • 즉, 최우원리는 평균치라는 통계량과 연결되어 있다는 뜻입니다.
• 확률 p를 움직인다는 것은 현상이 일어나는 원인(타입)에 사전분포를 설정하고 그것을 변화시키는 것과 매우 흡사합니다.
• 따라서 이 최우추정량이라는 사고법은 베이즈 추정의 발상과 공통되는 것이라고 이해할 수 있습니다.

• 위의 예제는 표준통계학에서의 최우원리를 사용한 예제이고 이 원리를 이용하면 베이즈 통계학과 공통된 사상이 있음을 알 수 있습니다.

정리

• 최우원리란 관측된 현상이 이러날 확률이 가장 커지는 원인을 선택하는 원리 입니다.
• 베이즈통계학의 사전확률은 최우원리를 응용한 한 가지 형태라고 볼 수 있습니다.
• 표준 통계학의 점추정에서는 관측된 현상의 확률을 최대한으로 하는 함수를 추정치로 사용합니다. 이것도 최우원리를 응용한 것입니다.
• 따라서 표준 통계학과 베이즈 통계학은 최우 원리라는 공통된 사상이 있습니다.