(베이즈 통계학 기초) 복수의 정보를 얻었을 때의 추정(1)

직면한 현상의 귀결에 복수의 가능성이 있어서 각각의 가능성에 확률을 할당할 수 있는 경우 그 현상을 시행 이라고 합니다.
- 예를 들어 주사위를 던져서 나올 수 있는 눈의 가능성은 복수개 이기 때문이 시행이라고 합니다.
만약 두 종류의 시행이 있을 때, 그 두 가지를 묶어 그것을 또 다른 시행으로 본다면 그 귀결에 대한 각각의 확률은 어떻게 되는지 알아보겠습니다.
예를 들어 제 1시행은 동전 던지기이고 제 2시행은 주사위 던지기라면 제 1시행과 제 2시행을 결합하여 제 3 시행을 만들 수 있습니다.
이와 같은 시행을 직적시행이라고 하는데, 이 용어는 격자 모양에 시행을 늘어 놓았다는 의미입니다.

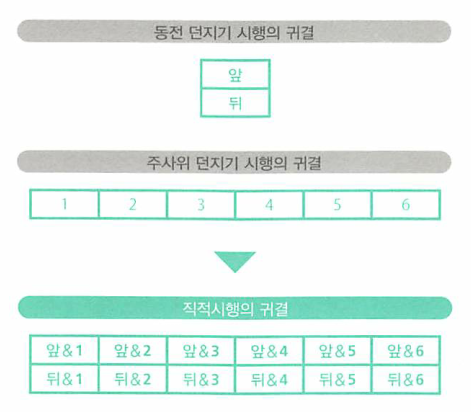
$Drawing$

두 개의 시행이 독립되어 있다는 것은 한쪽 시행의 귀결이 다른 쪽 시행의 귀결에 영향을 주지 않는 다는 것을 뜻합니다.
예를 들어 동전 던지기는 일반적으로 독립이라고 볼 수 있습니다. 왜냐하면 앞의 시행이 현재 시행에 영향을 주지 않기 때문입니다.
반면 서울의 비올 확률과 수원의 비올 확률은 완전히 독립이라고 할 수 없습니다. 왜냐하면 지리적으로 인접해 있기 때문에 한쪽이 비 올 확률이 높으면 다른쪽도 높을 수 있기 때문입니다.
- 이런 상태를 독립 시행과 반대로 종속 시행이라고 합니다.

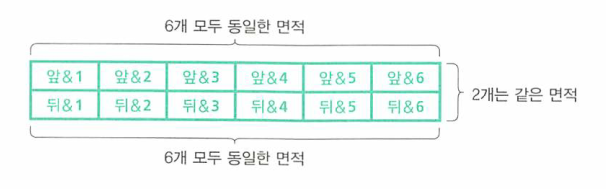
$Drawing$

위 그림을 보면 동전의 앞면이 나왔을 때의 주사위의 눈이 나올 확률과 동전의 뒷면이 나왔을 때의 주사위의 눈이 나올 확률이 정확히 일치 합니다.
즉, 동전 던지기의 시행 결과가 주사위의 눈이 나올 확률에 영향을 끼치지 않는다는 뜻이 됩니다.
확률을 나타내는 직사각형 전체 면적을 1이라고 한다면 정규화 조건에 따라 각 격자는 1/12의 확률을 가집니다.
직사각형이 12개의 격자로 나뉘게 된 이유는 동전의 2가지 경우의 수와 주사위의 6가지 경우의 수를 곱한 것이기 때문입니다.

위의 동전 던지기와 주사위 던지기의 사례는 사실 굉장히 극단적인 사례입니다.
왜냐하면 동전 던지기도 시행의 확률이 모두 같고 주사위 던지기 또한 각 시행의 확률이 모두 같기 때문에 전체 직사각형 격자들의 넓이가 모두 1/12로 같았습니다.
이번에는 격자의 넓이가 다른 일반적인 케이스에 대하여 다루어보겠습니다.

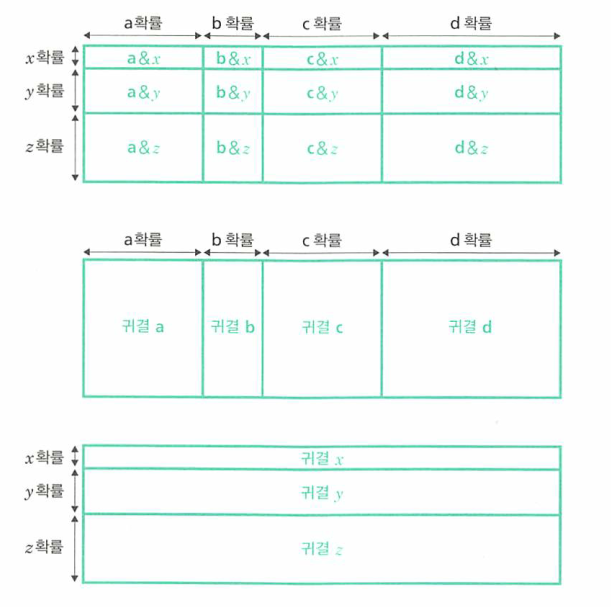
$Drawing$

위 예와 같이 제 1시행의 귀결은 a,b,c,d이고 제 2시행의 귀결은 x, y, z 라고 하겠습니다.
이 중 행 또는 열을 보면 격자의 넓이가 각각 다른 것을 볼 수 있습니다.
그러나 각 행 또는 열 내부에서의 시행 별 격자의 넓이(확률)는 동일한 것을 알 수 있습니다.
- 예를 들어 첫 번째 행과 두 번쨰 행 내부 격자의 대응되는 값들은 서로 똑같습니다. ($a$ : $b$ : $c$ : $d$)
즉, 제 1시행과 제 2시행은 서로 독립이란 것을 시각적으로 확인할 수 있습니다.
여기서 중요한 것은 독립 시행의 확률의 경우에는 위 처럼 직사각형 형태로 나타낼 수 있고, 각 시행의 확률이 격자의 가로 또는 세로의 길이가 되므로 격자의 넓이 = 가로 x 세로가 된다는 것입니다.
즉, 독립 시행에서의 복수의 시행 확률은 격자의 넓이를 구하듯이 각 시행의 확률을 서로 곱해주면 된다는 것입니다.
- 이 방식을 독립 시행 확률의 승법 공식 이라고 합니다.
- ex) (a & x 확률) = (a & x직사각형 면적) = (a확률) x (x확률)

정리하면 두 가지 시행을 묶은 직적시행은 직사각형을 격자 모양에 분할하여 그림으로 표시합니다.
두 가지 시행이 독립되어 있다는 것은 직관적으로 생각할 때, 한쪽의 귀결이 다른 쪽 귀결이 일어나는 데 영향을 주지 않는다는 것입니다.
두 가지 시행이 독립되어 있을 때, 다음과 같은 확률의 승법 공식이 성립합니다.
- 제 1시행의 귀결이 $a$ 이고 제 2시행의 귀결이 $b$이 x일 확률 = ($a$확률) * ($b$확률)