(베이즈 통계학 기초) 복수의 정보를 얻었을 때의 추정(2)

2019, Mar 03    

• 출처 : 세상에서 가장 쉬운 베이즈 통계학 입문

스팸메일 필터는 베이즈 추정에 기원한다.

• 이번 글부터 세 개의 글에서는 복수의 정보를 사용해서 베이즈 추정을 하는 벙법에 대하여 알아보려고 합니다.
• 먼저 이번 글에서는 두 개의 정보로 부터 사후 확률을 계산하는 방법에 대하여 알아보도록 하겠습니다.

• 이번 글에서 다루어 볼 예제는 스팸 메일 필터입니다.
• 일반적인 메일 서비스에 기본적으로 탑재되어 있는 기능이 스팸 메일 필터 기능입니다.
• 이 기능을 뒷받침해주는 이론적 배경이 바로 베이즈 추정입니다.

필터에 사전 확률을 설정합니다.

• 앞의 글에서 다룬 것 처럼, 사전 타입을 설정하고 하나의 정보를 얻은 뒤 사후 확률을 구해보겠습니다.
• 먼저 컴퓨터는 도착한 메일을 스캔하기 전에 그 메일이 스팸 메일인가 일반 메일인가하는 각 타입에 대한 사전 확률을 할당합니다.
• 여기에서는 이유 불충분의 원리를 적용하여 쌍방에 0.5씩 할당합니다.
• 만약 이 때, 이보다 신빙성 있는 데이터 및 확률이 있다면 그것을 사전확률(prior)로 사용하는 것이 좋습니다.
• 일단 사전 확률은 P(스팸메일) = 0.5, P(일반메일) = 0.5 입니다.

스캔할 글자나 문구와 그 조건부 확률을 설정합니다.

• 스팸메일에 자주 나오는 글자나 문구 혹은 특징들을 설정해 두어야 합니다.
• 예를 들어 다른 홈페이지의 URL 링크가 삽입되어 있다. 라는 특징이 있다고 생각해 보겠습니다.
• 그러면 URL 링크가 있다 → 대체로 스펨메일, URL 링크가 없다 → 대체로 일반 메일이라고 생각할 수 있습니다.
• 다시 한번 정리하면 사전확률은 스팸메일/일반메일에 대한 이미 알고있는 비율을 뜻합니다.
• 그리고 관측값(결과)는 관측 결과 스팸메일/일반메일인지를 뜻하고 조건(원인)은 URL이 있다/없다에 해당합니다.
  • 즉, 우리가 최종적으로 알고 싶은 것은 \(P(스팸메일 \vert URL 있음)\) 으로 URL이 있다 라는 원인이 있을 때, 스팸메일이란 결과의 확률 입니다.
  • 현재 우리가 관측한 것으로 알 수 있는 것은 반대로 \(P(URL 있음 \vert 스팸메일)\) 으로 스팸메일이다 라는 결과가 있을 때, 거기서 원인인 URL이 있을 확률 입니다.
• 만약 관측 가능한 메일들을 가져와서 스팸 메일과 일반 메일로 분류하고 스팸 메일 중에 URL이 있는 것과 없는것, 일반 메일 중에 URL이 있는 것과 없는 것으로 분류하여 비율을 구했을 때 다음과 같다고 가정해 보겠습니다.

• 위 확률 분포는 URL이 있을 확률입니다.

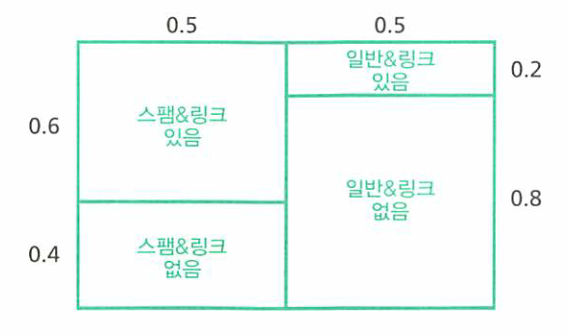
• 세로축의 0.5 / 0.5는 스팸 메일과 일반 메일의 사전 확률입니다. 사전 데이터가 없으므로 이유 불충분 원리로 인하여 0.5씩 할당하였습니다.

스캔 결과 스펨메일의 베이즈 역확률이 구해진다.

• 만약 새로운 메일이 들어 왔고 메일의 문장을 스캔한 결과 URL이 있다라고 관측하였다고 하겠습니다.
• 그러면 가능한 케이스가 아래와 같이 압축 됩니다.

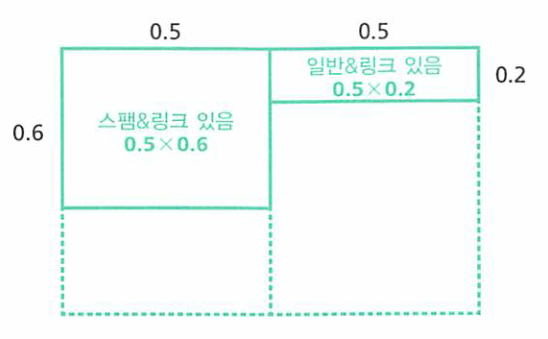
• 여기서 정규화 조건을 해주고 사후확률을 구하면 다음과 같습니다.
• (스팸메일일 사후확률) : (일반메일일 사후확률) = 0.5 x 0.6 : 0.5 x 0.2 = 3 : 1 = 3/4 : 1/4
• 따라서 링크가 있을 때, 스팸메일을 확률은 3/4가 됩니다.
• 스캔하기 전에는 이유 불충분 원리에 따라서 스팸메일일 확률이 0.5였는데 스캔 후에는 URL이 있다는 정보만으로 스팸메일일 확률이 0.75로 상승하였습니다.
• 물론 아직 이 경우에도 일반메일일 확률은 0.25가 남아있어서 완전히 스팸메일이라고 확정할 수는 없습니다.
• 만약 사후확률 0.95 이상으로 스팸메일이라고 예측되면 스팸메일로 넣어도 될거라고 추정할 수는 있습니다.

• 지금까지는 스팸메일인지 아닌지에 대한 조건으로 URL만 관여를 하였는데, 만약 만남이라는 단어를 같이 스캔한다면 어떻게 적용할 수 있을지 살펴보겠습니다.

• 만남이라는 단어가 있을 확률과 없을 확률이 위 표와 같다고 가정해 보겠습니다.
• 그러면 변수가 2개가 있는데요, URL이 있을/없을 확률 그리고 만남이 있을/없을 확률 입니다.
• 그러면 총 3개의 분기점인 스팸/URL/만남 으로 인하여 8가지의 경우의 수가 발생합니다.

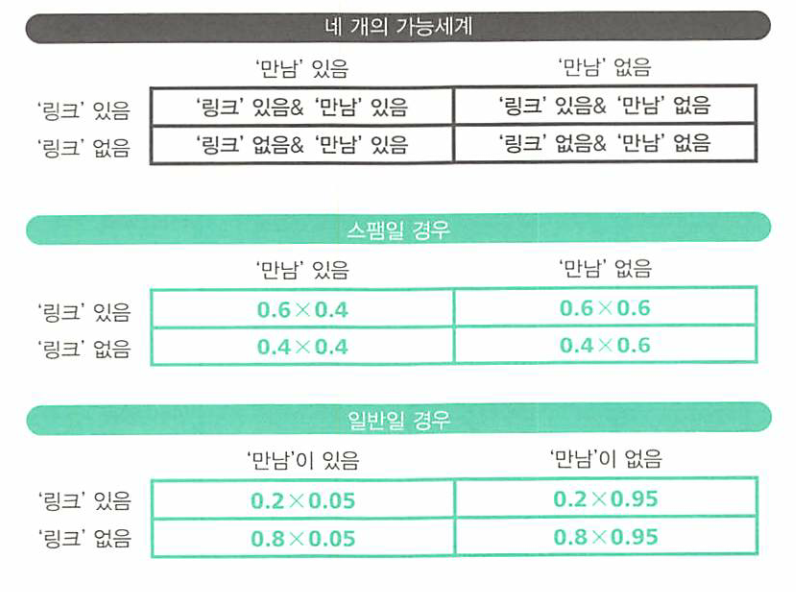
• 위 표에서 추가적으로 스팸/일반메일의 확률인 0.5도 곱해주어야 합니다.

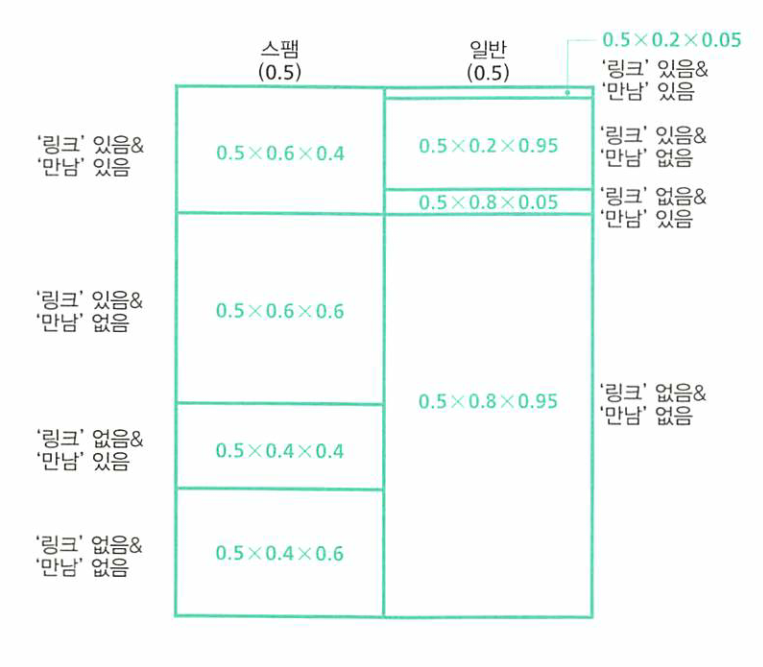
• 그러면 위와 같이 8개로 분기된 영역을 볼 수 있습니디.

두 가지 정보로부터 일어날 가능성이 없는 영역을 소거합니다.

• 만약 어떤 메일을 스캔하였을 때, URL이 있고 만남이라는 단어도 있으면 확률이 어떻게 되는지 보겠습니다.

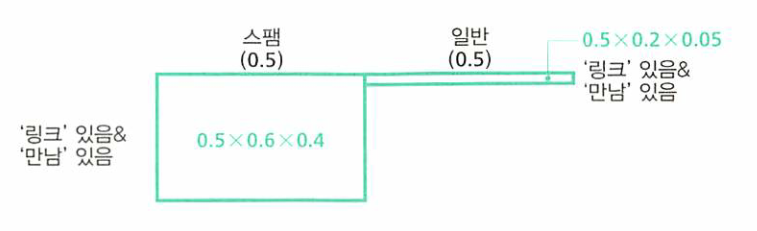
• 위 표에 정규화 조건을 적용하여 정리를 하면 스팸메일과 일반메일에 대한 확률은 다음과 같습니다.
• (스펨메일일 사후확률) : (일반메일일 사후확률) = 24/25 : 1/25
• 따라서 스펨메일일 사후확률은 0.96입니다.
• 만약 스팸메일 필터 설계를 스팸메일일 확률이 0.95이면 스팸메일함으로 이동시키도록 하였다면 이 사후확률의 결과 스팸메일 함으로 이동되게 됩니다.

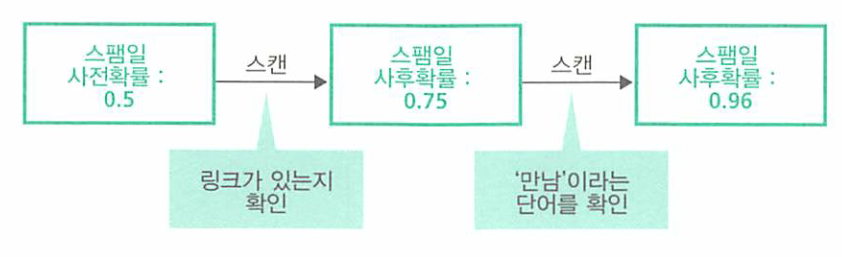
• 따라서 하나의 정보를 사용하여 판정할 때 보다, 두 개의 정보를 사용하여 판정할 때가 스팸메일의 가능성을 훨씬 높은 수치로 검출 할 수 있음을 알 수 있습니다.