(베이즈 통계학 기초) 베이즈 추정은 정보를 얻을수록 더 정확해집니다.

• 출처 : 세상에서 가장 쉬운 베이즈 통계학 입문

적당적당한 추측에서 더 정확한 추정으로 만들려면

• 앞에서 배운 베이즈 추정들을 통해 보면 대략적이라는 측면은 있지만 없는 것보다 훨씬 나은 추정 방법임을 계속 확인하였습니다.
• 그 대략이란 것은 사전확률에 기인합니다. 사전 확률은 아무런 정보가 없기 때문에 일단 대등한 것으로 설정합니다. (이유 불충분의 원리)
• 사전확률을 이런 방식으로 설정한 덕분에 데이터가 적어도 추정이 가능한 이점이 생겼습니다.
  • 베이즈 추정이 네이만-피어슨 식 추정보다 편리한 이유가 이 점이기도 합니다.
• 뿐만 아니라 베이즈 추정에서는 추정에 사용한 정보를 일단 사후확률에 반영시킨 뒤에는 버려도 관계없다는 성질이 있습니다.
  • 이것은 베이즈 추정의 학습 기능이라고 이전 글에서 다루었습니다.

• 이번 글에서 다룰 베이즈 추정의 한가지 특징 중 하나는 정보가 많아질수록 더 정확한 추정을 한다는 성질입니다.

• 이전 글에서 다루었던 단지에서 흰색/검은색 공을 꺼내는 문제를 다시 다루어 보겠습니다.
• 다루었던 문제는 다음과 같습니다.

눈앞에 상자가 하나 있는데, 상자 A나 B중 하나임을 알고 있지만 겉으로 봐서는 어느 쪽인지 알 수가 없습니다.
상자 A에는 흰 공 9개와 검은 공 1개가 있고 상자 B에는 흰공 2개와 검은공 8개가 있습니다.
이 때 상자에서 공을 한 개 꺼냈더니 검은공이었습니다. 어떤 상자에서 고른 것 일까요?

• 이전 글의 사후확률을 계산하는 과정을 참조하면 꺼낸 공이 검은 공이었을 때, A상자에서 꺼냈을 사후확률은 약 1/9, B상자에서 꺼냈을 사후확률은 약 8/9 였습니다.
• 여기서 추가 정보를 적용해 보겠습니다. 맨 처음 꺼낸 공을 다시 상자에 넣고 새로이 공을 한 개 뽑은 경우를 추정해 보겠습니다.
  • 첫번째 공의 색깔과 두번째 공의 색깔이라는 정보를 사용한 추정입니다.
• 먼저 상자가 A인지, B인지에 대한 정보가 전혀 없으므로 이유 불충분의 원리를 이용하여 0.5씩 사전 확률을 설정해 놓겠습니다.
• 예를 들어 다음과 같은 케이스를 생각해 보겠습니다. 첫 번째가 검은 공이고 두 번째가 흰공일 경우입니다.
• 흑&백일 확률 = (흑일 확률) x (백일 확률)
  • 만약 A 상자라면, 흑&백일 확률 = (흑일 확률) x (백일 확률) = 0.1 x 0.9 = 0.09
  • 만약 B 상자라면, 흑&백일 확률 = (흑일 확률) x (백일 확률) = 0.8 x 0.2 = 0.16
• 이러한 경우들을 직사각형 형태로 나타내면 다음과 같습니다.

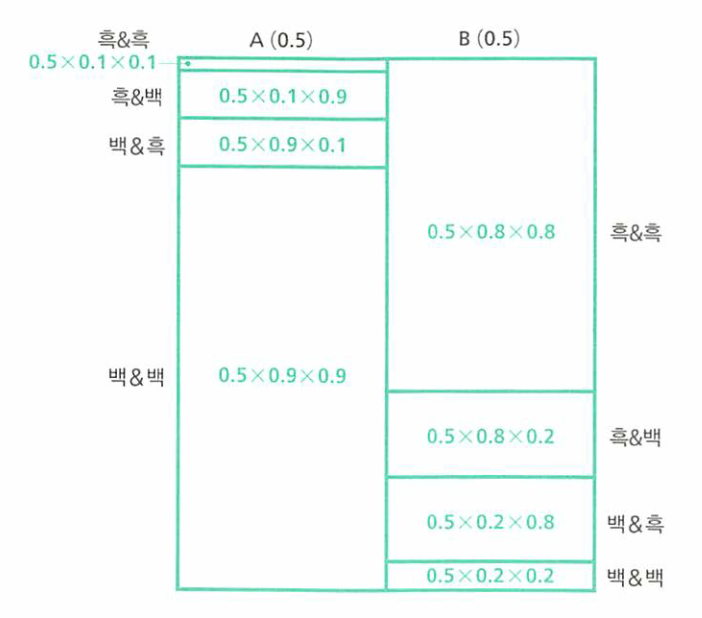
• A,B 상자라는 경우와 2가지 복원 추출의 경우로 8가지의 영역으로 구분되어집니다.

두번 째도 검은 공이었을 경우

• 만약 두 번째 공도 검은 색이라면 어떻게 될까요? 즉, 흑&흑의 경우의 수를 살펴보겠습니다. 이 경우에는 흑&흑 이외의 모든 조건은 소멸됩니다.

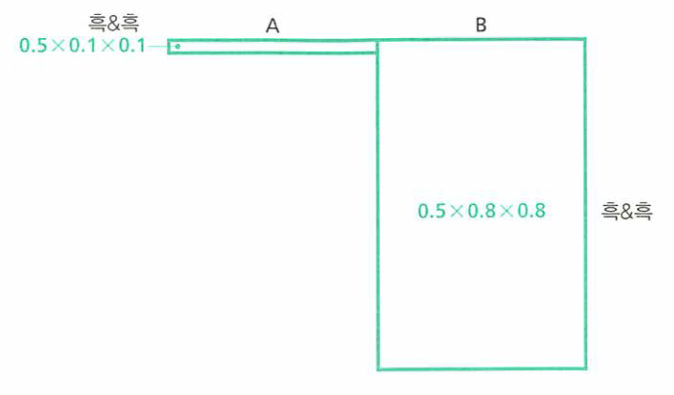
• 그림에서 정규화 조건을 충족하게 하면 사후 확률은 (흑&흑일 때 상자 A일 확률) : (흑&흑일 때 상자 B일 확률) = 1/65 : 64/65가 됩니다.
• 이와 같은 사후확률을 알고 있다면 상자가 B상자일 것이라고 추정할 수 있습니다.

• 여기서 중요한 것은 공을 꺼내는 시행을 할 수록 사후확률이 증가했다는 것입니다.
• 처음에는 정보가 전혀 없어서 0.5였던 확률이 한번 추출의 시행으로 0.89까지 올랐다가 추출을 한번 더 하니 0.98까지 상승하였습니다.
  • 즉, 여기서는 두번째도 같은 색깔의 공이었다는 사실이 맨 처음 추정 결과를 강화시켜준 것입니다.

두번 째는 흰 공이었을 경우

• 두 번째는 흰공이었을 경우를 확인하기 위해 흑&백 조합을 빼고는 모두 지워보겠습니다.

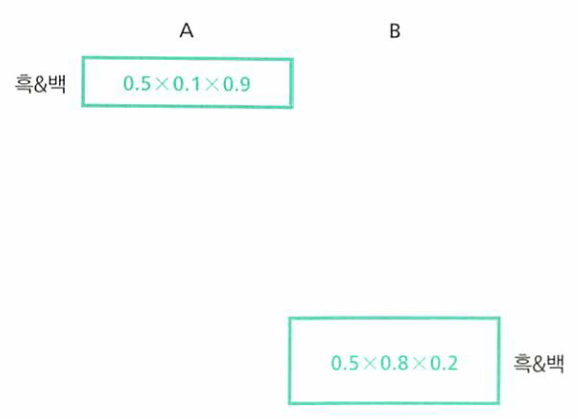
• 위 조건을 정리하여 정규화 조건을 적용시켜 보면 (흑&백일 때 상자A일 사후확률) : (흑&백일 때 상자B일 사후확률) = 0.36 : 0.64가 됩니다.

• 이 결과를 해석하면 첫 번째 추출에서는 검은 공이 나왔기 때문에 B 상자일 것이라는 추측이 컷지만(0.89), 두 번째에는 흰 공이 나와서 그 추측이 다소 떨어졌다고(0.64) 볼 수 있습니다.

최신 관측 결과에 따라 결론이 달라집니다.

• 앞에서 설명한 바와 같이 검은 공이 관측되면 상자 B일 사후확률이 커지며 흰공이 관측되면 상자 A일 확률이 커집니다.
  • 상자 A는 압도적으로 흰 공이 많고 상자 B는 압도적으로 검은 공이 많으므로 자연스러운 일입니다.

• 위 그림은 정보로부터 추정 결과가 어느 쪽으로 기우는지 나타냅니다.
• 구체적으로 어떤 계산으로 a와 b가 바뀌어 가는지 살펴보도록 하겠습니다.
• 현재 n번까지의 추정 결과 상자 A일 사후확률을 a라고 하고 상자 B일 사후확률을 b라고 하겠습니다. 이 때, (n+1)번째 검은 공인 경우 추정은 어떻게 이루어 질 지 알아보겠습니다.
• 베이즈 추정의 축차합리성에 따르면 (n+1)번째 사후확률을 계산하기 위하여 그때까지 나온 n번의 공을 열거할 필요는 전혀 없습니다.
  • 이미 n번째 사후확률에 전부 반영되어 있으므로 n번째의 사후확률(단지 A → a, 단지 B → b)을 사전확률로 설정하면 됩니다.
• 만약 (n+1)번째 공을 관측하였을 때 검은공이라면 이 때 뽑은 상자가 A일 확률을 a’, 상자 B일 확률을 b’ 라고 하고 n번째인 경우의 케이스를 각각 a, b 라고 한다면
  • (n+1번째가 검은 공일 때의 상자 A일 확률) : (n+1번째가 검은 공일 때의 상자 B일 확률)
  • = a’ : b’ = a x 0.1 : b x 0.8 = a : 8b
  • = a / (a+8b) : 8b / (a+8b)
• 관계를 보면 a’:b’ = a : 8b 인 것 처럼 b쪽만 8배의 비례관계가 되었습니다.
• 추이를 이해해 보면 a’는 a보다 작아지고 b’는 b보다 커지게 된 것이지요.

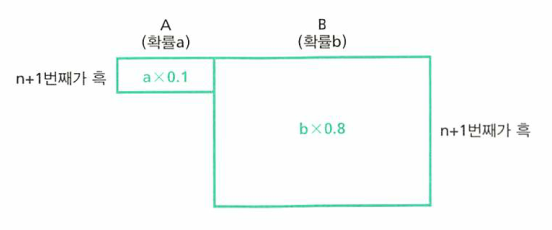
• 즉 위와 같이, (n+1)번째가 검은 공이었을 때, 확률 변화를 가지게 됩니다.
• 이와 유사하게 (n+1)번째가 흰공이었으면 a’는 a보다 커지게 되고 b’는 b보다 작아지게 됩니다.

여러번 관측할수록 추측은 진실에 가까워집니다.

• 앞의 해석에 따르면 n번째 공의 관측으로 상자 A일 사후확률이 a, B일 사후확률이 b라고 한 경우, n+1번째에서 검은 공이 관측되었다면 사후 확률의 비례관계 a:b → a:8b가 되었음을 확인하였습니다.
• 이것은 상자 B일 것이라는 의심이 더 강해진 것이지요.
• 이것은 상자 A에서 검은 공이 관측될 확률이 0.1임에 비해 B에서 관측될 확률이 0.8로 여덟배가 크다는 점이 반영되었기 때문입니다.
• 만약 관측된 공이 흰공이고 눈앞에 관측된 상자가 B였으면, 비록 낮은 확률로 흰공을 관측하였지만 관측을 계속할수록 검은공을 관측할 확률이 많이 높아질 것입니다.
• 관측을 계속할수록 b는 1에 계속 가까워질 것이고 a는 0에 계속 가까워져서 상자 B라고 추측하게 될 것입니다.

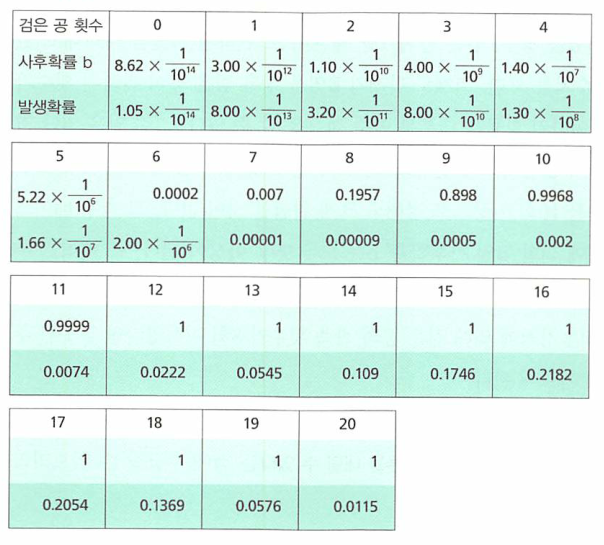
• 위 도표는 공을 20회 관측하였을 때, 검은 공이 나온 횟수에 대응하여 상자가 B일 확률이 몇이 되는가를 도표로 나타낸 것입니다.
  • 예를 들어 검은 공이 6번 나온 경우에 상자가 B일 사후확률은 0.0002입니다. 즉 검은공이 20회 중에 6번 나오며 상자 B일 확률은 엄청나게 낮은 확률입니다.
  • 반면 검은공이 9회 나온 경우에 상자B일 사후확률은 0.898입니다. 꽤 높은 확률입니다.

• 여기서 우리가 알고 싶은 것, 사후확률은 상자 B라면 검은 공이 나오는 횟수가 어느 정도 일까? 라는 것입니다.
• 발생확률 수치를 보면 9회 이하는 확률이 아주 아주 낮습니다. 따라서 검은 공이 관측될 확률은 10회이상이라고 해도 괜찮을 것 같습니다.
  • 물론 아주 낮은 확률로 검은 공의 관측 횟수가 8회 이하 정도라면 잘못된 추정이 된다는 리스크는 가지고 있지요.
• 여기서 얻을 수 있는 교훈은 베이즈 추정은 관측을 많이 하면 할수록 정확한 결론을 내릴 수 있다입니다.

• 정리해 보겠습니다.
• 베이즈 추정은 관측된 정보에 따라 판단이 흔들리는 상태를 나타냅니다.
• 즉, 검은 공이 관측되면 검은 공이 많은 상자 쪽으로 판단이 기울고 흰 공이 관측되면 흰 공이 많은 상자쪽으로 판단이 기웁니다.
• 이런 추정을 정확하게 만들려면 정보가 대량으로 있어야 하고 대량의 정보가 있으면 올바른 결정으로 이끌 수 있습니다.