(베이즈 통계학 기초) '확률'은 '면적'과 동일한 성질을 지닌다.

2019, Mar 03    

• 출처 : 세상에서 가장 쉬운 베이즈 통계학 입문

목차

• 확률은 함수의 형태로 기술한다.

• 확률은 면적과 동일한 성질을 지닌다.

• 베이즈 추정의 사전확률을 확률기호로 타나내면

• &로 연결된 사상을 확률기호로 나타내면

확률은 함수의 형태로 기술한다.

• 앞의 글들에서 베이즈 이론을 설명할 때, 수식이 아닌 면적도를 이용하여 설명하였습니다. 처음 배울때에는 그림으로 배우는 게 더 낫습니다.
• 하지만 일단 개념을 이해하면 기호로 설명하는 것이 덜 복잡합니다. 확률에 관한 간단한 기호를 살펴보겠습니다.
• 예를 들어 내일 날씨라는 것을 확률 모델로 나타내면 (맑음, 흐림, 눈, 비)로 나타낼 수 있습니다.
• 네 가지 사건에 각각 0 이상 1이하의 확률 값을 할당하고 네 가지 확률값을 모두 더했을 때 1이 되도록 만들면 정규화 조건을 만족하는 확률 모델이 됩니다.
  • 예를 들어 맑음: 0.3, 흐림: 0.4, 비: 0.2, 눈: 0.1
• 여기서 맑음, 흐림, 비, 눈을 근원사상이라고 합니다. 이 이상은 분해할 수 없는 가장 근본이 되는 사건이기 때문입니다.
• 근원사상을 몇가지 조합하면 사상을 만들 수 있습니다.
  • 예를 들어 (비, 눈)의 조합같은 집합이 될 수 있습니다.
• 이 사상을 확률로 표현하는 대표적인 방법은 p({맑음}) = 0.3 과 같은 방법입니다.
• 여기서 근원사상이 아닌 사상에 대한 확률은 그 사상을 구성하는 근원사상의 확률의 합으로 계산됩니다.
  • 예를 들어 p({비, 눈}) = p({비}) + p({눈}) = 0.3이 됩니다.
• 또한 사건이라는 개념이 나오는데, 이것은 근원사상을 몇가지 조합한 사상이 발생하는 상황입니다.
  • 예를 들면 우산을 사용한다라는 사건은 {눈, 비}라는 사상에 대응됩니다.
• 또 다른 예로 주사위의 예에서 근원사상은 {1}, {2}, {3}, {4}, {5}, {6}이고 짝수라는 사건의 `사상은 {2, 4, 6}이 됩니다.
  • 식으로 표현하면 \(p(짝수) = p(\{2, 4, 6\}) = 1/6 + 1/6 + 1/6 = 1/2\)가 됩니다.

확률은 면적과 동일한 성질을 지닌다.

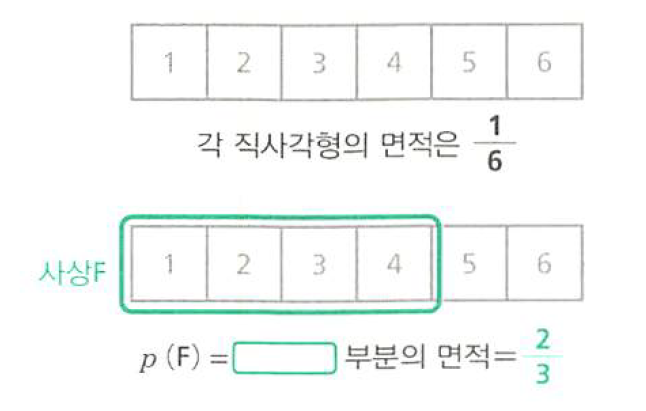
• 위에서 다룬 근원사상, 사상을 보면 확률은 면적과 같은 성질을 가지고 있음을 알 수 있습니다.
• 위의 그림을 보면 확률과 면적의 관계를 알 수 있습니다.
• 확률이 면적임을 이해하였다면 다음 성질들을 쉽게 이해하실 수 있을 것입니다.
• 확률의 덧셈법칙: 사상 A와 사상 B의 중첩되는 부분이 없다면, 즉 공통의 근원사상이 없다면 A 또는 B는 A의 확률과 B의 확률의 합과 같습니다.
  • 즉, \(p(A \ or \ B) = p(A) + p(B)\)

베이즈 추정의 사전확률을 확률기호로 타나내면

• 이전 글에서 다룬 예제인데 다시 한번 다루어 보겠습니다. 어느 부부로부터 태어날 아이가 딸일 확률을 다루어 보곘습니다.

• 만약 부부가 3가지 타입이 있고 각 타입에 따라 딸을 낳을 확률이 조사되었다고 가정해 보겠습니다.
• 그러면 위와 같이 prior를 세 영역으로 나눌 수 있습니다. 이 때, 3가지 타입이 있다는 것만 알고 그 비율을 모른다고 하면 이유불충분 원리를 통하여 균등하게 prior를 배분할 수 있습니다.
• 여기서 첫번째 타입은 딸을 낳을 확률이 0.4, 두번째 타입은 0.5, 세번째 타입은 0.6이라고 하겠습니다.
• 여기서 재밌는 점은 \(p(\{0.4\}) = 1/3\)으로 표현할 수 있다는 것입니다. 앞에서 보면 { } 사이에 들어갈 수 있는 것은 근원사상이었습니다.
• 그러면 여기서 {0.4} 라는것은 0.4라는 확률치가 근원사상이라는 것을 뜻합니다.
• 첫번째 타입 이라는 사건과 딸을 낳을 확률 0.4라는 사상을 이해하시면 됩니다. 그러면 \(p({0.4}) = 1/3\) 즉, 딸을 낳을 확률이 0.4일 확률은 1/3임을 이해하실 수 있습니다.

&로 연결된 사상을 확률기호로 나타내면

• &로 연결된 사상의 확률을 앞에서 직적시행 또는 확률의 곱으로 다루었었습니다.

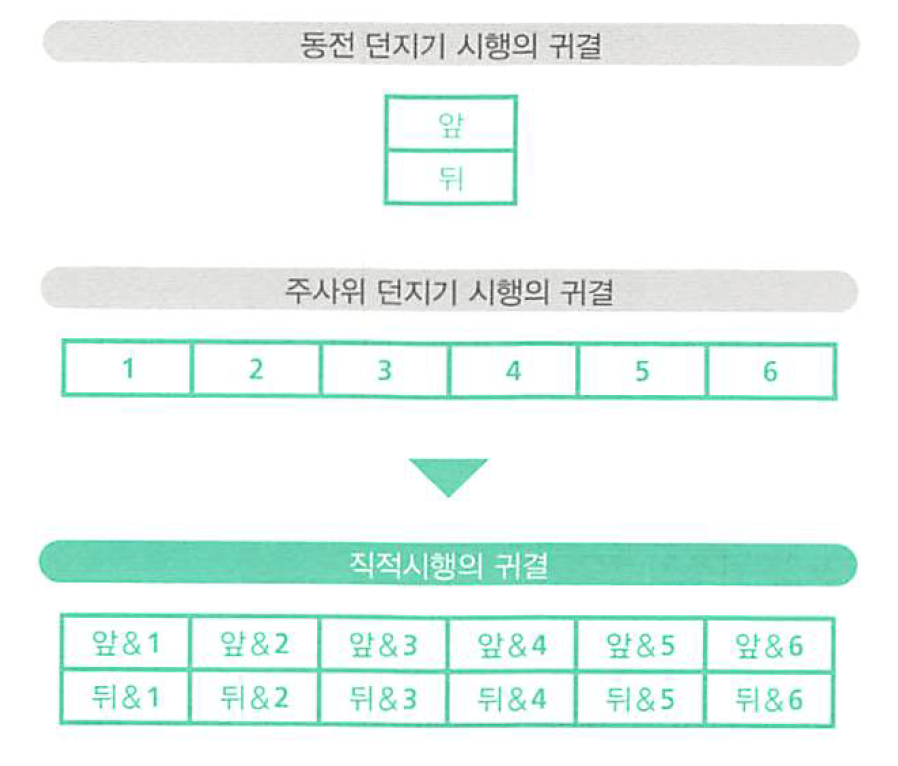
• 여러 시행의 결과를 & 조건으로 결합하여 새로운 시행을 만들 수 있는데 예를 들어 위와 같이 동전과 주사위를 던져서 생긴 두 시행의 결합 12개를 만들 수 있습니다.
• 이렇게 발생한 새로운 시행이 새로운 근원사상이 됩니다. 즉, 두 시행의 & 결과로 새로운 근원사상이 만들어졌습니다.
  • 예를 들면 {앞 & 2} 가 근원사상 중 하나가 될 수 있습니다.
• 그러면 여기서 {2} = {2 & 앞, 2 & 뒤} 이므로 {2} 는 사상이 됩니다.

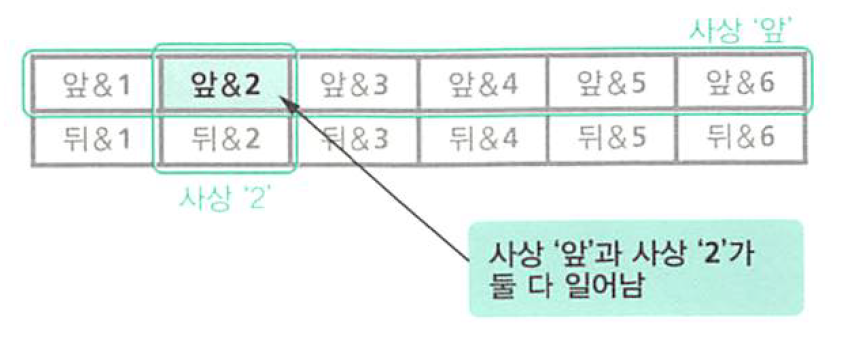
• 이렇게 결합되 사상 확률을 칸의 면적에 대응시켜서 볼 수 있습니다.
• & 조건으로 결합된 확률의 사상은 확률의 곱의 분포를 따르기 때문에 다음과 같이 표현될 수 있습니다.
  • p(동전 던지기의 결과 & 주사위 던지기의 결과) = p(동전 던지기의 결과)p(주사위 던지기의 결과)

정리

• 앞에서 배운 내용을 최종 정리해 보겠습니다.
• 확률 모델은 근원사상, 사상, 확률에 의하여 구성됩니다.
• 근원사상이란 이 이상 분해할 수 없는 근본적인 사건을 말합니다.
• 사상은 근원사상을 몇 가지 모아놓은 집합을 말합니다.
• 근원사상에 대해서 그 확률은 \(p({e})\)로 나타냅니다.
• 예를 들어 근원사상 \(e, g, f\)로 구성된 사상 \(e, g, f\)의 확률은 \(p(\{e, g, f\}) = p(\{e\}) + p(\{g\}) + p(\{f\})\)가 됩니다.
• 확률의 가법법칙이란 A와 B가 중첩되지 않을 사상일 때, \(p(A \ or \ B) = p(A) + p(B)\)가 성립하는 것입니다.
• 두 가지 확률현상을 결합하여 만드는 직적시행은 a & b와 같은 근원 사상으로 이루어져 있으며, 이 확률은 통상 독립시행으로 가정되어 곱 연산이 됩니다.
  • 즉, \(p(\{ a \& b \}) = p(\{ a \}) \times p(\{ b \})\) 입니다.