
(베이즈 통계학 기초) 정보를 얻은 후 확률의 표시법
2019, Mar 03
목차
-
조건부 확률이란 부분을 전체로 간주하여 수치를 수정하는것
-
타입이 부여된 확률 = 조건부 확률
-
조건부 확률의 공식을 통해 사후확률 이해
조건부 확률이란 부분을 전체로 간주하여 수치를 수정하는것
- 베이즈 추정에서 가장 중요한 사고법은 정보를 얻었을 때 확률이 변화한다는 것입니다.
- 정보의 유무와 종류에 따라 확률이 달라지는데, 그것을 기술하는 것이 바로
조건부 확률입니다. - 이번 글에서는
조건부 확률을 이용하여 베이즈 확률을 표현해 보도록 하곘습니다.
- 주사위 던지기 예를 들어 한번 설명해 보겠습니다. 먼저 주사위 눈이 짝수라는 사상은 \(E = \{2, 4, 6 \}\)으로 표현할 수 있습니다.
- 사상 \(E\)의 확률은 \(p(E) = \frac{3}{6} = \frac{1}{2}\)가 됩니다.
- 이 때, 6은 안나온다라는 정보를 얻게 되었다면 이 조건을 반영한 확률이
조건부 확률이 됩니다. - 먼저 6이 아니다 라는 사상을 \(F = \{1, 2, 3, 4, 5 \}\) 라고 하면 사상 F가 일어났다는 정보하에 사상 E의 확률을 구해야 합니다.
[p(E \vert F)]
- 여기 수식에서 \(\vert\) 기호의 오른쪽이 얻은 정보를 나타냅니다.
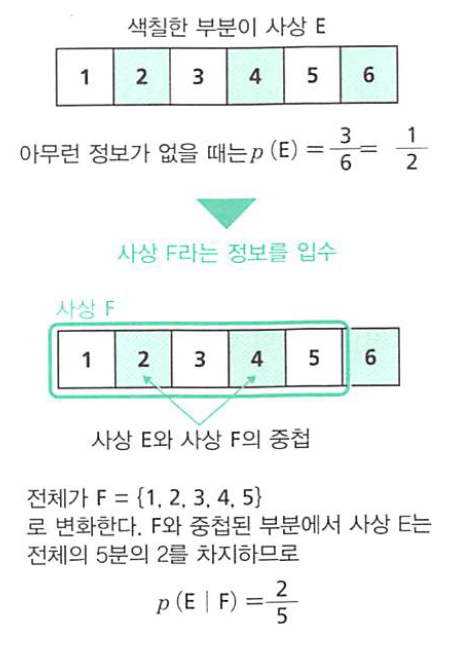
- 아무런 정보가 없었을 때에는 사상 \(E\)가 전체 면적의 절반을 차지하고 있었으므로 그 확률 \(p(E)\)는 1/2가 됩니다.
- 여기서 6이 아니다 라는 사상 \(F\)를 얻음으로써 전체 사상이 \(F\)로 변경된 점이 중요합니다.
- 변경점은 확률의 분자와 분모 각각에 발생합니다.
- 변경점1: 사상 \(F\)가 전체가 되었으므로 사상 \(F\)의 확률이 1로 설정되어야 합니다. 즉 \(F\)의 면적을 1로 간주합니다.
- 변경점2: 사상 \(F\)로 한정되었기 때문에 사상 \(E\)와 \(F\)의 공통부분에 한정하여 확률을 생각해야 합니다. 즉, 주목해야할 사상은 \(E\)와 \(F\)의 중첩인 \(\{2, 4 \}\)가 됩니다.
- 정리하면 \(p(E \vert F)\)는 사상 \(F\)가 일어났다는 정보하에서 \(E\)의 조건부 확률은, \(F\)를 전체로 생각하여 \(E\)와 \(F\)의 중첩이 \(F\)안에서 차지하는 비율이 됩니다.
- (E와 F가 중첩된 면적) / (F의 면적)
- 따라서 \(p(E \vert F) = p(\{2, 4\}) / p(\{1, 2, 3, 4, 5\}) = (2/6) / (5/6) = 2/5\)가 됩니다.
- 다시 한번 강조하면 조건부 확률이란 얻은 정보인 사상을 전체로 재설정하고, 가능성이 사라진 근원사상을 없애서 비율을 새로 정하는 것입니다.