What is a probability distribution

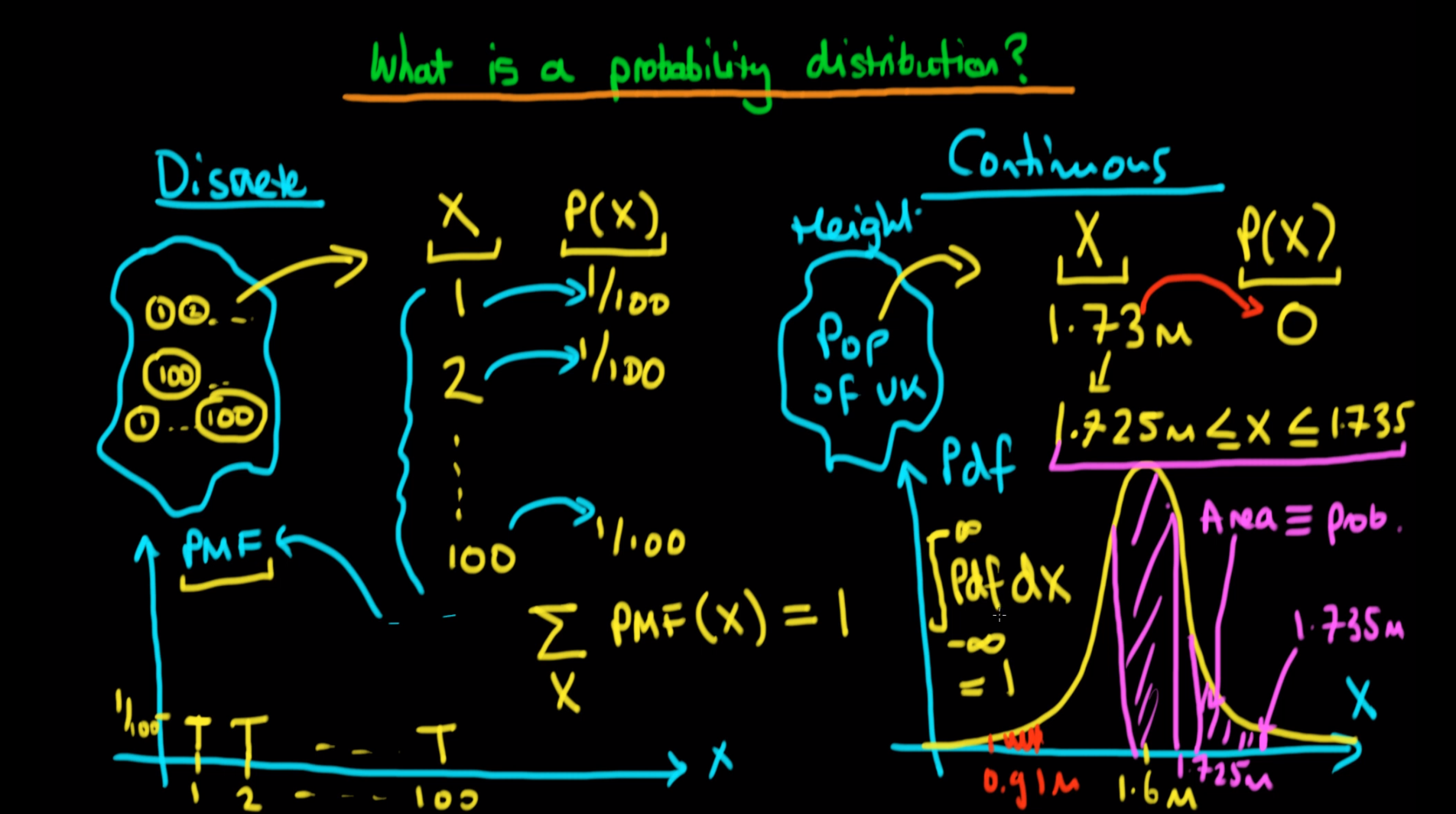
$Drawing$

이번 강의는 간단하게 확률 분포가 무엇인지 알아보는 내용이었습니다.
특히 이번 강의의 키워드인 discrete한 변수에서는 PMF(Probability Mass Function)이라는 용어가 나왔고 continuous한 변수에서는 PDF(Probability Density Function)라는 용어가 나왔습니다.
위 슬라이드에서 볼 수 있듯이 discrete한 변수에는 각 변수 당 발생할 확률이 정해져 있고 모든 변수가 나올 확률을 다 더했을 때 1이 되어야 합니다.
- 즉, $\sum_{x} pmf(x) = 1$ 이 됩니다.
위 예제에서는 모든 변수가 발생할 확률이 동등하고 이런 경우 uniform하다고 합니다.

반면, continuous한 변수에서는 각 변수 당 발생할 확률은 0에 수렴합니다. 위 슬라이드의 예 처럼 키가 정확히 1.73m 인 사람을 뽑을 확률은 거의 0에 가깝습니다. 1.731m, 1.732m인 사람은 해당되지 않으니까요.
이렇게 continuous한 변수를 가지는 분포에서는 정확히 어떤 변수에 대하여 확률이 대응되기 보다는 구간을 이용하여 확률을 구합니다.
따라서 PDF의 D가 뜻하는 Density처럼 얼마나 빽빽하게 분포되어 있는 지에 해당하는 밀도가 바로 확률에 해당합니다.
물론 PDF에서도 전체 Density를 합하면 1이 되어야 합니다.
- 즉, $\int_{-\infty}^{\infty} PDF(x) dx = 1$이 되어야 합니다.