베타 분포

• 출처 :
  • Probability & Statistics for Engineers & Scientists. 9th Edition.(Walpole 저. PEARSON)
  • 수리통계학 (김수택 저. 자유 아카데미)
• 통계학 관련 글 목록

베타 함수의 정의

• 베타 함수는 $\alpha, \beta > 0$ 일 때, $B(\alpha, \beta) = \int_{0}^{1} x^{\alpha-1}(1-x)^{\beta-1} dx$ 로 정의 됩니다.

베타 함수의 성질

• ·$\alpha, \beta > 0$ 범위에서
• ·$B(\alpha, \beta) = B(\beta, \alpha)$
  • 베타 함수에서 $\alpha, \beta$는 서로 자리를 바꾸어도 치환을 하여 적분식을 풀면 결과는 같습니다.
• ·$B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}$
  • ·$\Gamma(\alpha) = \int_{0}^{\infty}e^{-s}s^{\alpha-1}ds$ 정의를 따르면,
  • ·$\Gamma(\alpha)\Gamma(\beta) = \int_{0}^{\infty}e^{-s}s^{\alpha-1}ds \int_{0}^{\infty}e^{-t}t^{\beta-1}dt$
  • ·$= \int_{0}^{\infty}\int_{0}^{\infty} e^{-(s+t)}s^{\alpha-1}t^{\beta-1} dsdt$
  • 변수변환으로 $s = xy, t = x(1-y)$ 라고 하면 치환 적분처럼 생각할 수 있습니다.
    • 치환 적분을 하면 변수의 영역이 $s, t$ 에서 $x, y$ 로 변환됩니다.
      • 이 때, 자코비안의 절대값을 곱해주어야 합니다. (다중적분의 변수변환 참조)
    • s, t에 대한 x, y의 자코비안을 구해보겠습니다.
    • ·$J = \frac{\partial(s,t)}{\partial(x,y)} = \begin{vmatrix} \frac{\partial s}{\partial x} & \frac{\partial s}{\partial y} \\ \frac{\partial t}{\partial x} & \frac{\partial t}{\partial y} \\ \end{vmatrix} = \begin{vmatrix} y & x \\ 1-y & x \end{vmatrix} = -xy -x + xy = -x$
      • 마지막으로 절대값을 취해주면 $\vert -x \vert = x$입니다.
  • ·$s = xy, t = x(1-y)$ 에서 적분의 범위를 살펴보면 s와 t의 범위가 0 ~ 무한대이므로
    • x의 범위는 0 ~ 무한대 입니다.
    • y = 1인 경우 t = 0, s는 무한대의 범위를 가질 수 있습니다.
    • y = 0인 경우 s = 0, t는 무한대의 범위를 가질 수 있습니다.
    • 즉, y = 0 과 1의 값을 경계로 s와 t가 0 ~ 무한대 범위를 가집니다.
    • 따라서, y의 범위는 0 ~ 1, x의 범위는 0 ~ 무한대 입니다.
  • ·$\Gamma(\alpha)\Gamma(\beta) = \int_{0}^{\infty}\int_{0}^{1} e^{-x} (xy)^{\alpha-1}(x(1-y))^{\beta-1} x \ dydx$
  • ·$= \int_{0}^{\infty}e^{-x}x^{\alpha + \beta - 1} dx \int_{0}^{1}y^{\alpha-1}(1-y)^{\beta-1}$
  • ·$= \Gamma(\alpha + \beta)B(\alpha, \beta)$

베타 분포

• 확률밀도함수가 $f(x; \alpha, \beta) = \frac{1}{B(\alpha, \beta)}x^{\alpha - 1}(1-x)^{\beta-1}$
  • 이 때, $0 < x < 1$ 이고 $\alpha, \beta > 0$ 일 때,
  • 모수가 $\alpha, \beta$ 인 베타분포라고 합니다.
  • 이 때, $\frac{1}{B(\alpha, \beta)}$는 면적을 1로 만들기 위한 정규화 입니다.
  • 형태가 이항 분포와 비슷합니다. 이항 분포는 이산 확률 변수에 관한 확률이고 이항 분포에 대응하는 연속 확률 변수의 확률이 베타 분포입니다.
    • 예를 들어, 전체 시간 중에 x를 하는 시간 또는 전체 물질의 양 중에 x의 비율 등이 있습니다.
• 
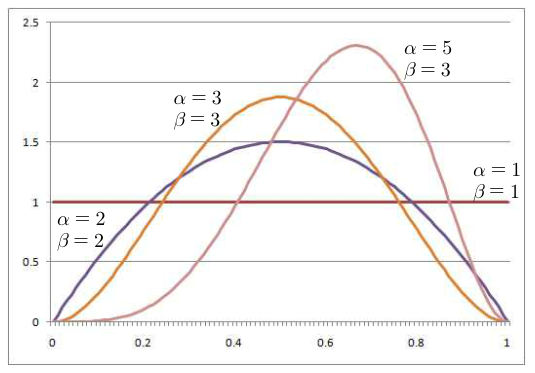
  • 그래프의 x축을 보면 $0 < x < 1$ 구간에서의 분포입니다.
  • ·$\alpha = \beta = 1$ 이면, $f(x; \alpha, \beta) =$
    • $0 < x < 1$ : 1
    • 그 이외의 $x$ : 0
    • 균일 분포(uniform distribution)을 가집니다.
  • ·$\alpha = \beta$인 경우 $x = \frac{1}{2}$ 중심으로 좌우대칭 입니다.
  • ·$\alpha < \beta$ 이면 왼쪽으로, $\alpha > \beta$ 이면 오른쪽으로 치우칩니다.
  • ·$c < X < d$인 구간에서의 베타분포 : $x^{*} = \frac{x - c}{d - c}$로 변환하면 $0 < x^{*} < 1$ 입니다.
    • 범위를 0 ~ 1까지 맞춰주기 위해서 변환해 줍니다.

베타 분포의 예제

• 석유 도매상에서 매주 석유를 공급 받는데, 일주일 동안 공급량에 대한 판매량의 비율을 관찰한 결과 근사적으로 $\alpha = 2, \beta = 2$인 베타분포를 따르고 있었다.
• 도매상에서 어느 한주일 동안 공급량의 90% 이상을 판매하게 될 확률을 구하여라.
  • 한주일 동안 판매량 비율을 X라고 하면, 확률밀도함수는
  • ·$f(x) = \frac{1}{B(4,2)}x^{3}(1-x)^{1} = \frac{\Gamma(6)}{\Gamma(4)\Gamma(2)}(x^{3} - x^{4}) = \frac{5!}{3!1!}(x^{3} - x^{4}) = 20(x^{3} - x^{4}) (0 < x < 1)$
  • ·$P(X > 0.9) = \int_{0.9}^{1}f(x) dx = \int_{0.9}^{1} 20(x^{3} - x^{4}) dx = [5x^{4} - 4x^{5}]_{0.9}^{1} \approx 0.08$

베타분포와 이항분포의 관계

• ·$\alpha, \beta$가 양의 정수이고 $n = \alpha + \beta -1$ 일 때, 확률 변수 X는 모수 $\alpha, \beta$인 베타분포를 따르고
• 확률 변수 Y는 성공률 p의 n회 시행인 이항분포를 따르면 다음이 성립 합니다.

[P(X \le p) = P(Y \ge \alpha)]

• 증명은 다소 복잡하여 생략하겠으나 중요한 점은 이산형 베타분포는 이항분포와 연관이 있음을 기억해야 합니다.