
중심 극한 이론
2020, Jan 02
- 출처 : https://youtu.be/JNm3M9cqWyc
- 이번 글에서는
중심 극한 이론(Central Limit Theorem)에 대하여 알아보도록 하겠습니다.
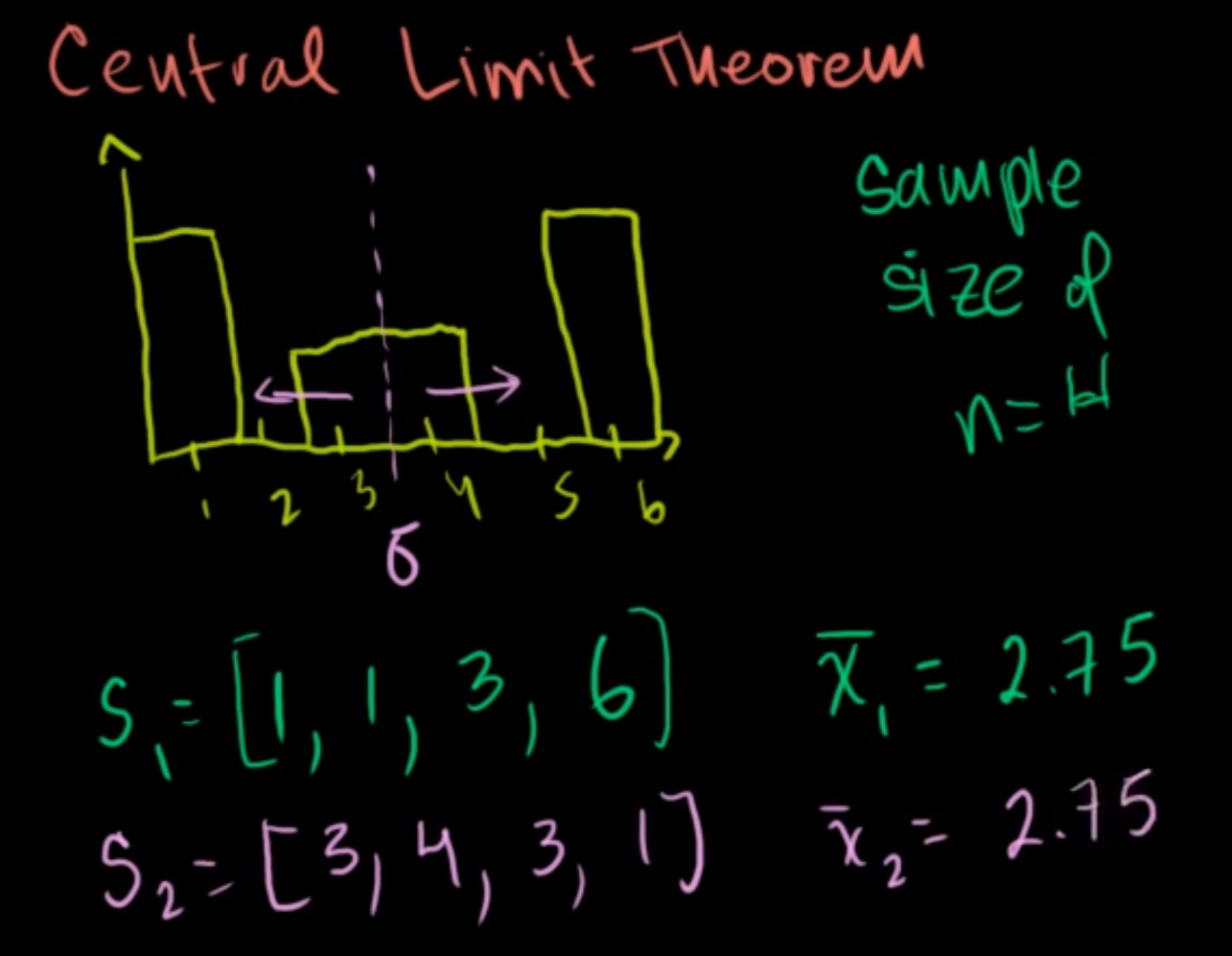
- 만약 위 노란색 그래프 처럼 확률 값을 가지는 확률 분포가 있다고 가정하겠습니다.
- 전체 발생 가능한 사상은 1, 3, 4, 6이고 1과 6의 발생 확률이 높고 3과 4의 발생 확률이 조금 낮습니다.
- 이 확률 분포에서 4번 샘플링 한다고 가정하겠습니다.
- 예를 들어 첫번째 샘플은 위 그림처럼 1, 1, 3, 6일 수 있습니다. 이 때, 샘플링된 표본의 평균은 2.75입니다.
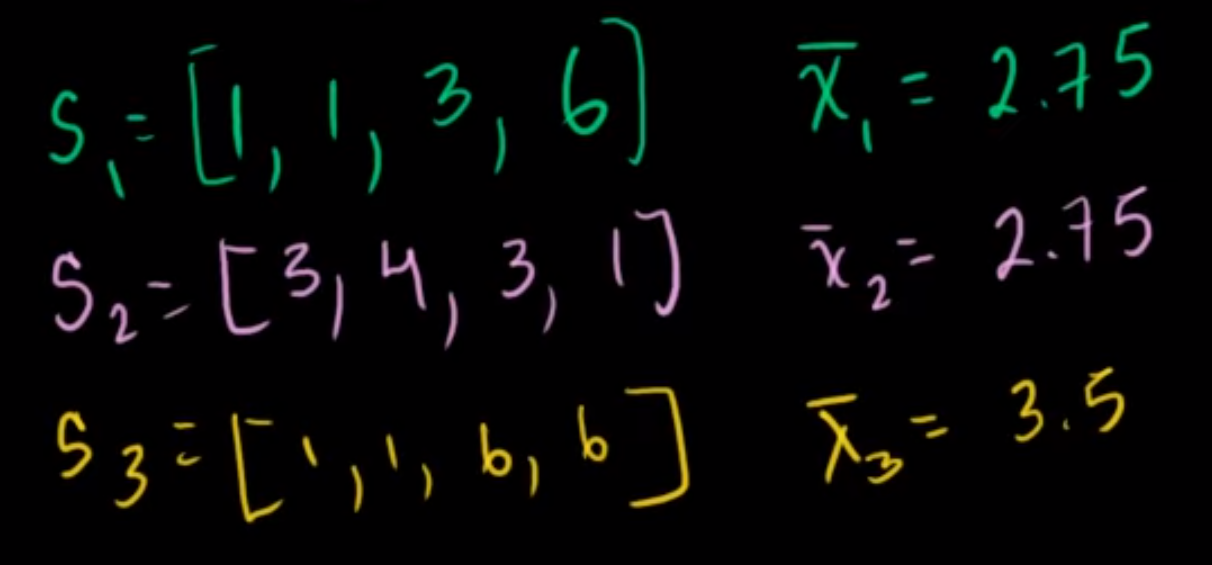
- 추가적으로 샘플링을 더 하여 두번째 샘플들, 세번째 샘플들 등을 뽑을 수 있습니다.
- 그러면 1이 4번 뽑히는 경우 표본 평균은 1, 6이 4번 뽑히는 경우 표본 평균은 6이고 이 사이의 표본 평균들이 샘플을 할 때 마다 발생하게 됩니다.
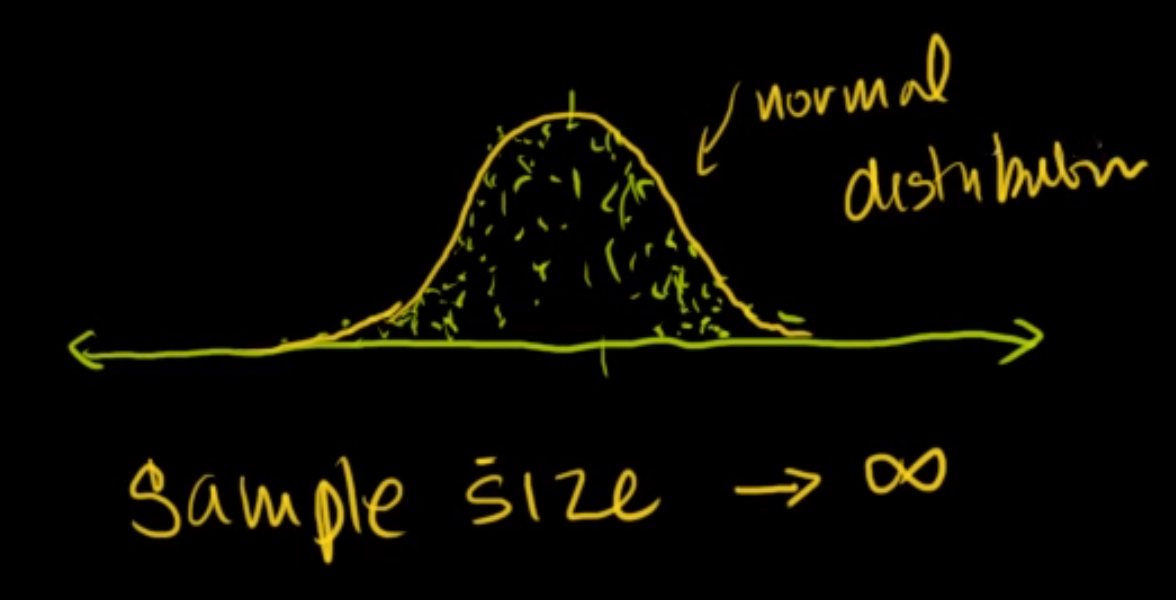
- 이 샘플링을 계속하면 위와 같은 분포를 띄게 되는데 정규 분포의 형태를 따르게 됩니다.
- 샘플의 사이즈를 더 크게 가질수록 점점 더 정규 분포의 형태를 따라가게 됩니다.
중심 극한 이론은 이와 같이 어떤 확률 분포를 가지더라도 샘플링을 계속하였을 때, 그 샘플링한 표본들의 평균은 정규 분포의 형태를 따른다.는 성질입니다.- 이러한 성질을 이용하면 분포를 모르거나 또는 계산하기 어려운 분포의 경우 중심 극한 이론의 원리에 따라 정규 분포로 근사 시켜서 사용할 수 있습니다.
- 정규 분포는 그 특성상 다양한 성질 및 편의성이 있기에 근사해서 사용할 경우 상당한 장점이 많습니다.
- 제 블로그에서 가우시안 분포 관련 글들을 참조해서 그 장점들을 한번 찾아보시길 바랍니다.