Statistical modeling, Bayesian modeling, Monte carlo estimation, Markov chain.

2020, Mar 15    

• 통계학 관련 글 목록

• 이번 글에서는 Statistical modeling, Bayesian modeling, Monte carlo estimation 그리고 Markov chain 까지 연계해서 다루어보도록 하겠습니다.

목차

• Statistical model이란?

• Modeling process

• Components of Bayesian models

• Model specification

• Posterior derivation

• Non-conjugate models

• Monte Carlo integration

• Monte Carlo error and marginalization

• Computing examples (with Python)

Statistical model이란?

• statistical model이 무엇일까요? statistical model은 데이터 생성 과정을 모델링 한 것입니다. statistical model은 다양한 변수들의 관계에 대하여 설명하는데 이 변수들은 데이터 속에서 매우 다양하게 나타나고 불확실하게 나타나는 특성을 가집니다.
• 예를 들어 변수들이 너무 다양하거나 변수들의 관계가 너무 복잡하면 변수들 간의 관계를 알아차리기가 어려워 random behavior 형태로 데이터가 나타날 수 있습니다.
• 이러한 random behavior들의 불확실성과 다양성을 나타내기 위해서는 확률 이론을 도입해서 나타낼 수 있습니다. 이 때 사용하는 것이 바로 statistical model이 됩니다.
• statistical model의 첫번째 목적은 불확실성의 정량화(quantify uncerntainty)입니다.
  • 예를 들어 투표를 하였을 때, 투표율이 57% 라고 한다면 이 데이터를 정확히 믿을 수 있을까요? 어떤 집단에서 어떻게 뽑았느냐에 따라서 데이터의 정합성이 달라질 수 있습니다. 만약 99%의 신뢰도로 (51%, 63%) 범위의 투표율을 가진다고 표현한다면 좀 더 적합해 보입니다. 즉, 불확실성에 대한 수치를 정량화 함으로써 막연한 데이터를 좀 더 수치적으로 표현할 수 있고 좀 더 많은 정보를 얻을 수 있습니다.
• statistical model의 두번째 목적은 어떤 가정에 대한 근거를 마련하기 위함입니다.
  • 예를 들어 어떤 후보에 대한 지지율이 여성들은 55%, 남성들은 59%이므로 남성들이 더 선호한다 와 같이 근거를 마련하는 데 사용됩니다.
• statistical model의 세번째 목적은 예측(prediction)입니다. 사실 이 목적으로 저희는 statistical model을 많이 사용합니다.
  • 다양한 변수들을 조합하였을 때, 어떤 후보의 지지율이 가장 높을 지 예측 하거나 어떤 변수들을 조합하였을 때, 이런 패턴의 투표자들은 어떤 후보를 뽑을 지 등등 다양한 예측을 하는데 statistical model이 사용됩니다. 특히 이러한 방법들을 machine learning 으로 사용되는데 machine learning의 주 목적인 prediction을 하는데 model이 사용됩니다.

Modeling process

• 그러면 statistical model을 어떻게 모델링 하는 지 스텝 별로 차례대로 알아보도록 하겠습니다.
• ① Understand the problem
  • 모델을 정의하기 전에 분석해야 할 문제를 정확히 이해해야 합니다. 예를 들어 여러 데이터를 모았는데 단위가 다르다면 모델링이 시작부터 잘못될 수도 있습니다.
• ② Plan & Collect data
  • 어떻게 데이터를 모으고 얼마나 많이 모을 지 계획해야 합니다. 어떤 계획을 세워서 데이터를 모으느냐에 따라서 데이터의 질이 달라집니다. 특히 데이터가 다양한 케이스를 모두 포함시킬 수 있도록 하려면 계획을 잘 세우지 않으면 특정 케이스만 모이게 될 가능성이 높습니다.
• ③ Explore your data
  • 수집한 데이터를 시각화하여 데이터를 이해하는 단계입니다. 이 단계에서는 데이터에서 나타나는 변수들 간의 관계에 대하여 살펴보고 어떤 statistical model을 사용할 지 결정하기 위한 정확한 데이터 이해를 해야합니다.
• ④ Postulate model
  • 앞에서 데이터가 어떤 지 이해하였다면, 데이터를 잘 표현할 수 있는 모델을 선정해야합니다. 모델을 선정할 때에는 model complexity와 model generalizability의 tradeoff(bias - variance tradeoff)를 고려하여 선정해야 하는데 정확한 데이터에 대한 이해가 있으면 선정하는 데 도움이 됩니다. 즉, 복잡한 모델은 overfitting 문제를 만들 수 있는데 어느 정도 복잡한 모델을 사용할 지에 대한 기준은 데이터를 통해 정해야 합니다.
• ⑤ Fit model
  • 이 단계에서는 모델에서 사용되는 파라미터들을 추정해야 합니다. 이 글에서는 bayesian 방법으로 파라미터 추정을 할 예정입니다.
  • 정확히 이 단계에서 Bayesian과 Frequentist의 패러다임이 나뉘게 됩니다.
• ⑥ Check model
  • 선정한 모델과 파라미터 추정이 잘 되었는 지 확인하는 단계입니다. 적절한 metric을 이용하여 얼마나 데이터에 대한 일반화 성능이 좋은지 확인합니다.
• ⑦ Iterate ④, ⑤, ⑥
  • 더 좋은 성능을 내기 위하여 모델을 다시 선택하거나 (④) 파라미터 추정(⑤)을 다시해본 뒤 성능 측정(⑥)을 하는 과정을 반복합니다.
• ⑧ Use model
  • 수집한 데이터에 가장 적합한 모델과 파라미터를 찾았다면 이 모델을 사용합니다.

• 지금까지 statistical modeling이 무엇이고 어떤 과정을 거치는 것인 지 알아보았습니다.
• 앞에서 설명하던 중 Fit model을 할 때에 Bayesian 패러다임을 사용할 것이라고 말하였는데 지금부터 Bayesian modeling에 대하여 간략히 알아보도록 하겠습니다.

Components of Bayesian models

• 이번에는 주제를 바꿔서 bayesian modeling에 대하여 다루어 보도록 하겠습니다. 쉽게 예를 들어서 설명해 보겠습니다.
• 15명의 사람이 있고 이 사람들의 키가 정규 분포를 따른다고 가정해 보겠습니다. 그러면 다음 식처럼 분포를 정의할 수 있습니다.

• $$n = 15, \ \ \ \ y_{i} = \mu + \epsilon_{i}, \ \ \ \ \epsilon_{i} \sim N(0, \sigma^{2}) \dots ( ext{i.i.d})$$
• • $$y_{i} \sim N(\mu, \sigma^{2}) \dots ( ext{i.i.d})$$

• 위 식을 이용할 때, 여기 까지는 frequentist와 bayesian의 접근 방법이 같습니다.
• 여기 까지 frequentist의 접근 방법은 $\mu$와 $\sigma$를 알기 위해서 가지고 있는 표본을 이용하여 이 값들을 구하고 만약 샘플링을 다시 한다면 다시 계산하여 이 값을 구하는 방식을 이용합니다. 일반적인 사람들이 많이 사용하는 방법입니다.
• 반면 bayesian의 접근 방법은 $\mu$와 $\sigma$를 각각 고유한 확률 분포를 가지는 random variable로 다루는 방식입니다. 이 변수들을 각각 다룰 때, 이것을 prior 라고 합니다.
• 다시 정리하면 frequentist와 bayesian의 가장 큰 차이점은 다음과 같습니다.
  • frequentist : unknown paramter를 constant로 둔다.
  • bayesian : unkown paramter를 random variable로 둔다.
• 베이지안에는 크게 3가지 요소인 likelihood, prior, posterior가 있습니다.
• likelihood는 데이터에 대한 확률적 모델의 값입니다. 데이터에 대한 이란 의미에서는 데이터를 나타내는 파라미터 $\theta$로 표현할 수 있고 확률적 모델에서 확률 모델을 $y$ 라고 한다면 (확률 모델은 정규분포가 될 수도 있고 이항 분포가 될수도 있고 아니면 다양한 다른 다양한 분포가 될 수 있습니다.) likelihood는 다음과 같습니다.

• $$\text{likelihood} = p(y \vert \theta)$$

• prior는 데이터의 확률입니다. 앞에서 frequentist의 접근 방법에서 $\mu$와 $\sigma$ 값을 얻을 때, 단순히 주어진 데이터를 통해서 구한 것과 의미가 같습니다. frequentist의 방법에서는 $\mu$와 $\sigma$의 값이 목적이지만 prior는 그런 데이터가 나올 확률이 목적입니다.

• $$\text{prior} = p(\theta)$$

• 데이터가 나올 확률과 그 데이터에 대한 확률적 모델을 연관시켜서 보면 joint distribution 형태로 나타낼 수 있습니다.

• $$p(y, \theta) = p(\theta)p(y \vert \theta)$$

• posterior는 likelihood와 반대로 확률적 모델의 값에 대한 데이터의 확률입니다. 이 값은 앞에서 정의한 joint distribution을 이용하여 다음과 같이 표현할 수 있습니다.

• $$p(\theta \vert y) = \frac{p(\theta, y)}{p(y)} = \frac{p(\theta, y)}{\int p(\theta, y)d\theta} = \frac{p(y \vert \theta)p(\theta)}{\int p(y \vert \theta)p(\theta)d\theta}$$

• 위 식을 보면 조건부 확률로 분모가 $p(y)$가 되어 즉, 확률적 모델의 값이 $p(y)$가 되었을 때의 경우로 한정이 되고 그 때, 데이터 $\theta$가 나올 확률을 나타냅니다.
• 또한 위 식의 $\int$는 일반화 시키기 위해 사용한 식의 기호이며 이산 확률 변수의 경우 $\sum$으로 대체해도 됩니다.

Model specification

• 모델을 fitting 하기 전에 먼저 모든 구성 요소를 지정해야 합니다. 이를 위한 한 가지 편리한 방법은 모델을 계층적 형식(hierarchical form)으로 표현해 보는 것입니다. 즉, 계층별로 모델이 레이어(단계)에 지정되어 있음을 의미합니다.
• 앞에서 다룬 키에 관한 예제를 이용해서 다시 살펴보도록 하겠습니다.
• 먼저 random variable인 $y_{i} \vert \mu, \sigma^{2}$에 대하여 알아보겠습니다.

• $$y_{i} \vert \mu, \sigma^{2} \ \sim \ N(\mu, \sigma^{2}) \dots (\text{i.i.d}), \ \ \ i = 1, 2, ..., n$$

• 그 다음 prior에 대하여 알아보겠습니다. 이 때, $\mu$와 $\sigma$는 독립이라고 가정하겠습니다. 평균과 분산을 독립이라고 가정하였기 때문에 분리해서 표현할 수 있습니다.

• $$p(\mu, \sigma^{2}) = p(\mu)p(\sigma^{2})$$

• 그리고 $\sigma^{2}$의 값을 알면 $\mu$ 의 conjugate가 정규 분포이고, $\mu$가 알려져있을 때 $\sigma^{2}$ 의 conjugate가 inverse gamma distribution이라는 것이 알려져 있습니다. 따라서 다음과 같이 적어보겠습니다. 아래 파라미터의 인덱스 0은 단순히 숫자를 표시하기 위해 적었습니다.

• $$\mu \ \sim \ N(\mu_{0}, \sigma_{0}^{2})$$
• $$\sigma^{2} \ \sim \ \text{Inverse Gamma}(\nu_{0}, \beta_{0})$$

• 이제 위 식을 이용하여 prior 에서 likelihood 까지 어떻게 graphic 하게 표현해보겠습니다.

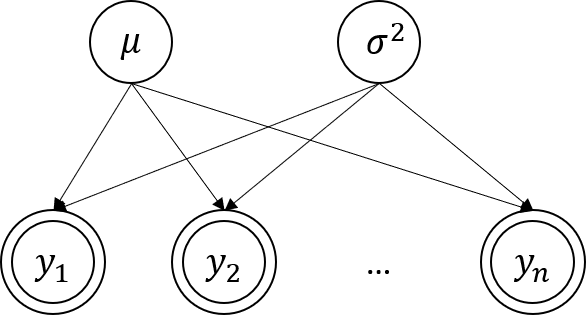
• 위 그림에서 한 개의 동그라미는 자체적으로 분포를 가지는 random variable 임을 뜻합니다.
• 두 개의 동그라미는 데이터에서 관측이 가능한 random variable임을 뜻합니다.
• 화살표의 뜻은 도착점의 random variable이 시작점의 random variable에 종속적이라는 뜻입니다. 즉, $y_{i}$는 -

• $\mu$와 $\sigma^{2}$에 종속적입니다.

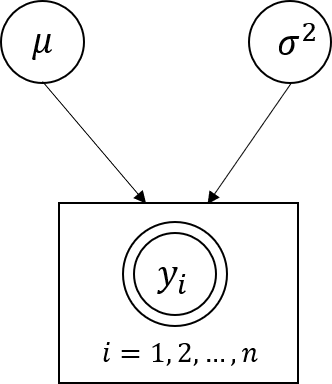
• 위 그림과 같이 정리해서 표현할 수도 있습니다.
• 위와 같이 graphic 하게 표현할 때, 시작점은 dependency가 없는 random variable에서 부터 시작하면 됩니다.
• 예제에서는 $\mu$와 $\sigma$가 그 시작점이 될 수 있고 이 시작점이 바로 prior가 됩니다.

• Posterior derivation

• Posterior에 대하여 알아보기 위해 다음과 같은 hierarchical model 예제를 정의해 보겠습니다.

• $$y_{i} \vert \mu, \sigma^{2} \sim N(\mu, \sigma^{2})$$
• $$\mu \vert \sigma^{2} \sim N(\mu_{0}, \sigma^{2})$$
• $$\sigma^{2} \sim \text{inverse gamma}(\nu_{0}, \beta_{0})$$

• 위 식을 그래프로 나타내면 다음과 같습니다.

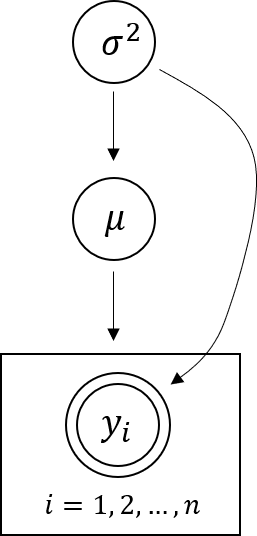
• 이 식을 joint distribution 형태로 나타내 보겠습니다.

• $$p(y_{1}, \cdots, y_{n}, \mu, \sigma^{2}) = p(y_{1}, \cdots, y_{n} \vert \mu, \sigma^{2})p(\mu \vert \sigma^{2})p(\sigma^{2}) = \prod_{i=1}^{n} = \Biggl( N(y_{i} \vert \mu, \sigma^{2}) \Biggr) \times N(\mu \vert \mu_{0}, \sigma^{2}) \times \text{inverse gamma}(\sigma^{2} \vert \nu_{0}, \beta_{0})$$

• 그리고 앞에서 다룬 베이즈 이론을 이용해 보겠습니다.

• $$p(\theta \vert y) = \frac{ p(y \vert \theta)p(\theta) }{ \int p(y \vert \theta)p(\theta) d\theta} \propto p(y \vert \theta)p(\theta)$$

• 베이즈 이론을 이용하면 prior와 likelihood의 곱은 posterior에 비례합니다. (분모는 확률의 값을 0과 1사이로 노말라이즈 해주는 역할 일 뿐입니다.)
• 그러면 앞에서 다룬 joint distribution인 $p(y_{1}, \cdots, y_{n}, \mu, \sigma^{2})$ 또한 다음과 같이 prior와 likelihood의 나타나지게 됩니다. $p(y_{1}, \cdots, y_{n} \vert \mu, \sigma^{2})p(\mu \vert \sigma^{2})p(\sigma^{2})$
• 따라서 joint probability, prior와 likelihood의 곱을 posterior와의 비례식으로 표현하면 다음과 같이 정리할 수 있습니다.

• $$p(y_{1}, \cdots, y_{n}, \mu, \sigma^{2}) = p(y_{1}, \cdots, y_{n} \vert \mu, \sigma^{2})p(\mu \vert \sigma^{2})p(\sigma^{2}) \propto p(\mu, \sigma^{2} \vert y_{1}, \cdots y_{n})$$

• 지금까지 살펴본 식들을 보면 prior는 $p(\theta )$가 되고 posterior는 $p(\theta \vert y)$가 됩니다.
• 즉, 기존에 가지고 있는 데이터에 대한 확률을 확률적 모델을 이용하여 업데이트 한 것이 됩니다.
• 이 때, prior와 posterior의 확률 분포는 동일한 확률분포를 뛸까요? 그런 경우도 있고 그렇지 않은 경우도 있습니다.
• 만약 prior와 posterior의 확률 분포가 같은 확률 분포족에 속한다면conjugate distribution 이라 하고 이 때의 prior를 conjugate prior 라고 합니다.
• 특히 몇몇 분포들은 closed form 형태로 conjugate distribution을 띄기 때문에 마치 점화식 형태로 표현 가능합니다.
• 하지만 많은 분포들은 Non-conjugate 관계를 가집니다. None-conjugate 관계를 가지면 어떻게 표현되는 지 알아보겠습니다.

Non-conjugate models

• 그러면 깔끔하게 conjugate distribution 형태를 가지지 않는 non-conjugate model을 살펴보겠습니다.
• 예를 들어 다음과 같습니다.

• $$y_{i} \vert \mu \ \sim \ N(\mu, 1)$$
• $$\mu \ ~ \ \frac{1}{\pi(1 + \mu^{2})}$$

• 위 식과 같은 계층 형식이 있다고 하면 posterior를 다음과 같이 적을 수 있습니다.
• 첫번째 식에서 $y_{i} \vert \mu$는 표준 정규 분포를 따른다고 하고 $\mu$는 두번째 식의 분포에 의해 샘플링 된다고 가정하겠습니다.

• $$p(\mu \vert y_{1}, \cdots , y_{n}) \ \propto \ \prod_{i=1}^{n} \Biggl( \frac{1}{\sqrt{2\pi}}\text{exp}(-\frac{1}{2}(y_{i} - \mu)^{2}) \Biggr)\frac{1}{\pi(1 + \mu^{2})} \\ \propto \text{exp}\Biggl( -\frac{1}{2} \sum_{i=1}^{n} (y_{i} - \mu)^{2} \Biggr) \frac{1}{\pi(1 + \mu^{2})} \\ \propto \text{exp} \Biggl( -\frac{1}{2}\Biggl( \sum_{i=1}^{n}y_{i}^{2} - 2\mu\sum_{i=1}^{n}y_{i} + n\mu^{2} \Biggr)\Biggr)\frac{1}{\pi(1 + \mu^{2})} \\ \propto \frac{\text{exp}\Biggl(n(\bar{y}\mu - \frac{\mu^{2}}{2}) \Biggr)}{1 + \mu^{2}}$$

• posterior는 위 식처럼 전개할 수 있습니다. 위 식의 결과는 prior와 상당히 다른 형태입니다. 즉, non-conjugate model의 예시가 됩니다.

• 심지어 파라미터의 갯수가 많아지고 prior와 likelihood의 식이 복잡해질수록 posterior는 non-conjugate가 되는 경향이 커지고 심지어 계산하기 어려울 정도로 식이 복잡해 지기도 합니다.
• 경우에 따라서는 식으로 나타나 지기도 어려운 경우가 생기기도 합니다.
• 이런 문제를 계산 하는 방법에 대하여 앞으로 다루어 보도록 하겠습니다.

• 여기 까지 개념을 정리하기 위해 다음 문제들을 한번 풀어보시길 권장합니다.

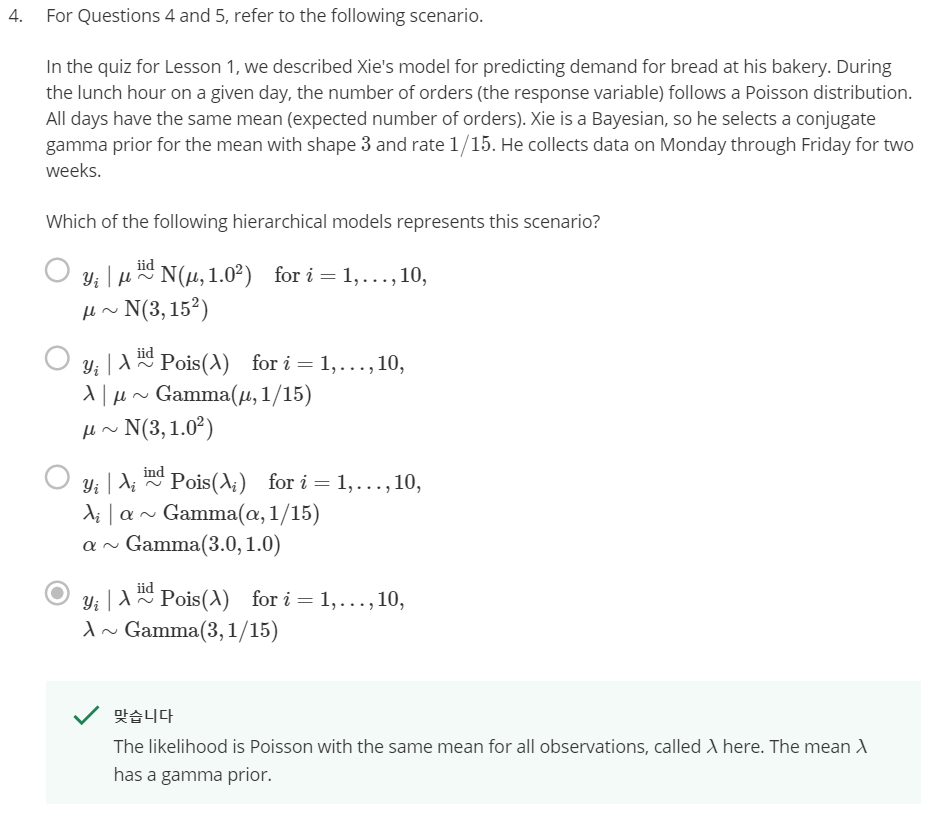
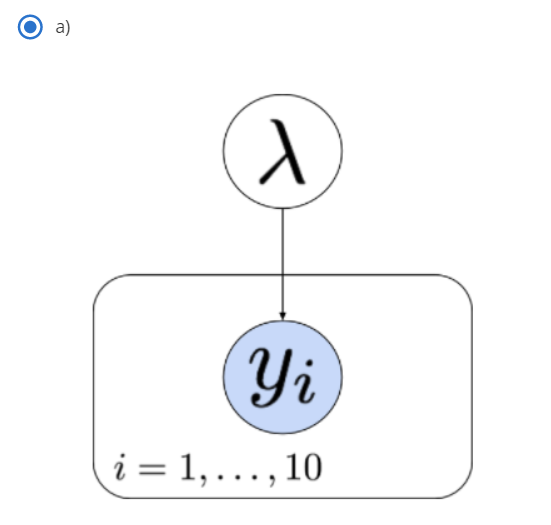
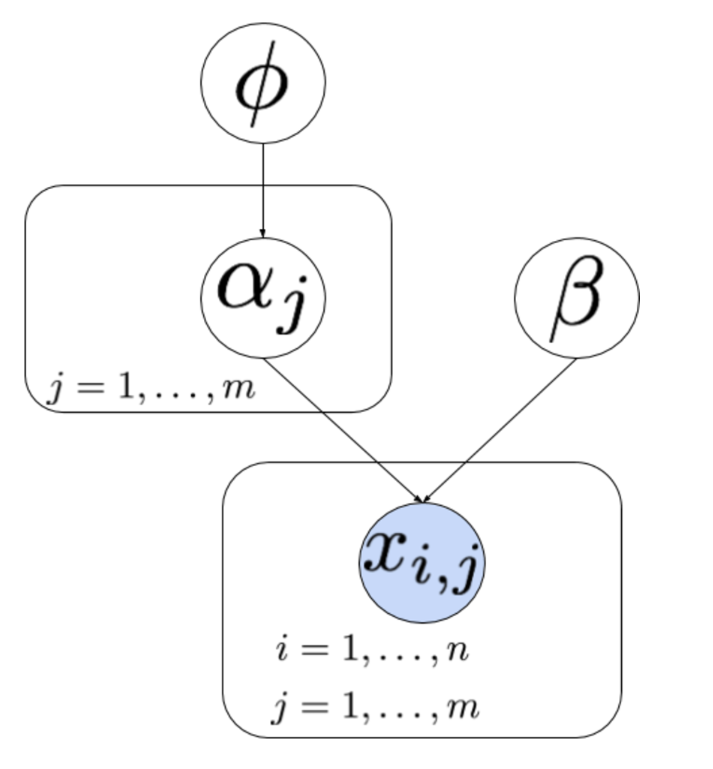
Monte Carlo integration

• 복잡한 posterior distribution을 시뮬레이션 하기 위해서 Monte Carlo estimation에 대하여 배워보도록 하겠습니다.
• Monte Carlo estimation은 확률 분포로 부터 도출한 시뮬레이션 방법입니다. 이 방법을 통하여 어떤 분포의 의미있는 값들을 (평균, 분산, 어떤 사건의 확률값등) 계산할 수 있습니다.
• 확률 값들을 계산하기 위해서 대부분 적분의 과정이 필요한 데, 쉬운 적분 방법이 있는 경우가 아니라면 계산이 매우 어렵거나 직접 계산하는 것이 불가능한 경우들이 있습니다.
• 예를 들어 다음과 같은 확률 변수 $theta$가 있다고 가정해 보겠습니다.

• $$\theta \ \sim \ \text{Gamma}(a, b)$$
• $$E(\theta) = \int_{0}^{\infty} \theta p(\theta) d\theta = \int_{0}^{\infty} \frac{b^{a}}{\Gamma(a)}\theta^{a-1}e^{-b\theta}d\theta = \frac{a}{b}$$

• 확률 변수 $\theta$는 감마 분포를 따른다고 하면 평균 값은 위 식과 같이 적분의 형태를 통한 기대값으로 나타낼 수 있고 알려진 대로 a/b로 정리할 수 있습니다.
• 사실 위 식을 직접 계산하려면 상당히 어려운데 어떻게 간단하게 a/b로 정리할 수 있을까요?

• $$\theta^{*}_{i} \ \ i = 1, \cdots m$$

• 여기서 $\theta^{*}_{i}$를 샘플링한 특정 확률 변수라고 두고 아주 큰 수 $m$ 까지 샘플링 한다고 해보겠습니다.

• $$\bar{\theta}^{*} = \frac{1}{m} \sum_{i = 1}^{m} \theta_{i}^{*}$$

• 아주 많은 갯수의 샘플링된 확률 변수를 사용하였기 때문에 큰 수의 법칙에 따라 $\bar{\theta}^{*}$는 정규분포를 따르고 이 표본 정규분포의 평균은 실제 평균 값 을 가집니다.
• 또한 샘플링된 확률 변수를 사용하여 구한 분산은 실제 분산을 $m$으로 나눈 값이 됩니다.

• $$\text{var}(\theta) = \int_{0}^{\infty}(\theta - E(\theta))^{2} p(\theta) d\theta$$

• 이론적으로 구한 분산이 위와 같으니 표본의 확률 변수에 대한 분산은 $\text{var}(\theta) / m$이 됩니다.
• Monte Carlo estimation을 통한 평균 계산을 정리하면 다음과 같습니다.

• $$\int h(\theta)p(\theta)d\theta = E[h(\theta)] \approx \frac{1}{m}\sum_{i=1}^{m}h(\theta_{i}^{*})$$

• 그러면 위 정의를 이용하여 다음 예제를 풀어보겠습니다. $I_{A}(\theta)$ 함수는 확률 변수 $\theta$가 조건 $A$를 만족하면 1을 반환하는 함수입니다.

• $$h(\theta) = I_{\theta < 5}(\theta)$$
• $$E(h(\theta)) = \int_{0}^{\infty} I_{\theta < 5}(\theta) p(\theta) d\theta = \int_{0}^{5} 1 \cdot p(\theta) d\theta + \int_{5}^{\infty} 0 \cdot p(\theta) d\theta = \text{Pr}[0 \gt \theta \gt 5] \approx \frac{1}{m} \sum_{i=1}^{m} I_{\theta^{*} < 5}(\theta_{i}^{*})$$

• 위 식의 마지막 항을 보면 얼마나 많은 $\theta^{*}$가 조건을 충족하는 지에 대한 평균을 내는 것이고 샘플링 횟수가 많아질수록 적분 형태의 이론적인 평균과 유사해짐을 나타냅니다.

Monte Carlo error and marginalization

• Monte Carlo 샘플링은 얼마나 좋은 방법일까요? 중심 극한 이론에 따르면 variance는 결국 샘플링한 사이즈 m에 영향을 받게 됩니다. 따라서 더 나은 예측을 하기 위해서는 m의 크기를 더 크게 잡는 것이 중요합니다.
• 예를 들어 $\theta$가 확률 변수이고 확률 변수의 표본을 $\theta^{*}$ 라고 한다면 표본 평균을 $\bar{\theta^{*}}$ 라 하고 표본 평균은 아래 식과 같은 분포를 따릅니다.

• $$\bar{\theta^{*}} \ \sim \ N(E(\theta) , \frac{var(\theta)}{m}$$

• 이 때, 표본 분산은 다음 식을 따릅니다.

• $$\bar{var(\theta)} = \frac{1}{m} \sum_{i=1}^{m} (\theta_{i}^{*} - \bar{\theta}^{*})^{2}$$

• 위 식에서 원래 m-1로 나누어야 합니다. (표본분산의 평균이 모분산과 같아지게 하기 위해서입니다.)
• 지금 다루는 m은 굉장히 큰 수라고 가정하기 때문에 m-1과 m으로 나눌 때의 큰 차이가 없으므로 편의상 m 이라고 사용하겠습니다.
• 이 때, Monte Carlo에서 다루는 standard error는 다음과 같습니다.

• $$\sqrt{\frac{\bar{var(\theta)}}{m} }$$

• 표본 분산을 표본의 크기로 나눈 다음에 다시 루트를 취해주는 형태입니다. 간단히 말해서 분산이란 얼마나 평균에서 떨어져 있는 지를 나타내므로 불확실성에 영향을 주는데 위 식에서 표본의 크기로 나누기 때문에 표본의 크기가 무한히 커진다면 standard error는 0에 수렴하게 됩니다.

• 이번에는 marginalization에 대하여 살펴보기 위해 다음 식을 예제로 살펴보겠습니다.

• $$y \vert \phi \ \sim \ \text{Bin}(10, \phi)$$
• $$\phi \ \sim \ \text{Beta}(2, 2)$$
• 위 분포를 이용하여 joint distribution을 만들면 다음과 같습니다.

• $$p(y, \phi) = p(\phi)p(\y \vert \phi)$$

• 그러면 Monte Carlo를 Simulation 하기 위한 절차는 다음과 같습니다.
• ① : Beta 분포로 부터 $\theta_{i}^{*}$를 샘플링 합니다.
• ② : 샘플링 한 $\theta_{i}^{*}$가 주어졌을 때, $y_{i}^{*}$를 $y_{i}^{*} \ \sim \ \text{Bin}(10, \phi_{i}^{*})$에서 도출합니다.
• ③ : ①, ② 과정을 통하여 $(y_{i}^{*}, \phi_{i}^{*})$의 쌍을 만들 수 있습니다.
• Monte Carlo Simulation의 가장 큰 장점 중 하나는 malginalization이 상당히 쉽다는 것입니다.
• 만약 $y$에 대한 malginal distribution을 직접 구한다면 계산이 상당히 복잡해 질 수 있습니다. 즉, $phi$에 대하여 적분이 필요한데 적분 계산 자체가 어렵기 때문입니다.
• 만약 joint distribution을 통하여 바로 샘플을 도출할 수 있다면 $\phi_{i}^{*}$를 이용한 계산을 하지 않아도 되고 \(y_{i]^{*}\)를 marginal distribution을 통하여 얻은 샘플로 바로 사용할 수 있습니다. (앞에서 다룬 prior predictive distribution 내용 입니다.)
• 그러면 이 성질을 이용해서 posterior distribution에 대한 근사 추정을 해보도록 하겠습니다.

Computing examples

• 앞에서 배운 내용에 대해 정리하면서 Python을 이용하여 예제들을 한번 풀어보도록 하겠습니다.

• 통계학 관련 글 목록