감마분포와 지수분포 (Gamma distribution and Exponential distribution)

2020, Apr 06    

• 통계학 관련 글 목록

목차

• 감마 함수

• 감마 분포와 지수 분포

• 감마 분포의 평균과 분산

• 지수 분포의 평균과 분산

• 포아송 과정과의 관계

• 확률 분포 정리

• 이번 글에서는 감마 분포와 지수 분포에 대하여 다루어 보려고 합니다.
• 감마 분포는 감마 함수와 연관되어 있어 이름이 감마 분포이고 지수 분포는 물론 지수 함수와 연관되어 있어 지수 분포 이름을 가지게 됩니다. 특히 지수 분포는 감마 분포의 특수한 경우에 해당됩니다.
• 감마 분포는 대표적으로 대기 시간이 얼마나 되는지, 어떤 사건이 발생할 때 까지 얼마나 많은 시간이 필요한 지 등에 사용되어 신뢰도에도 적용할 수 있습니다.

감마 함수

• 감마 함수는 $\alpha > 0$ 인 $\alpha$에 대하여 다음과 같이 정의 됩니다.

• $$\Gamma(\alpha) = \int_{0}^{\infty}x^{\alpha - 1}e^{-x} dx$$

• 위 감마 함수는 대표적으로 다음 성질이 성립합니다.
• ① $\alpha > 1$일 때, $\Gamma(\alpha) = (\alpha -1)\Gamma(\alpha - 1)$
• ② $\Gamma(1) = 1$이고 양의 정수 n에 대하여 $\Gamma(n) = (n - 1)!$
• ③ $\Gamma(\frac{1}{2}) = \sqrt{\pi}$

• 두 성질을 보면 감마 함수는 팩토리얼을 실수 범위로 확장한 것으로 해석할 수 있습니다.
• 그러면 위 2가지 성질에 대하여 증명을 해보도록 하겠습니다.

• 먼저 ① 식을 증명하기 위하여 부분 적분의 성질을 이용해 보도록 하겠습니다. 다음과 같습니다.

• $$\int f'(x)g(x) = f(x)g(x) - \int f(x)g'(x)$$

• 여기서 적분 하기 쉬운 것을 $f(x)$로 두겠습니다. $f(x) = e^{-x}$, $g(x) = x^{\alpha -1}$

• $$\Gamma(\alpha) = -x^{\alpha - 1}e^{-x}\vert^{\infty}_{0} + \int^{\infty}_{0} (\alpha - 1)x^{\alpha - 2}e^{-x} dx$$
• $$= (\alpha - 1)\Gamma(\alpha -1)$$

• 다음으로 ② 식을 증명해 보도록 하겠습니다.

• $$\Gamma(1) = \int_{0}^{\infty}e^{-x} dx = -e^{-x} \vert_{0}^{\infty} = 1$$

• $$\Gamma(n) = (n - 1)\Gamma(n-1) = (n - 1)(n - 2)\Gamma(n-3) = (n - 1)(n - 2) ... (1)\Gamma(1) = (n - 1)!$$

• 마지막으로 ③ 식에 대하여 다루어 보겠습니다. 실제로 감마 함수를 사용할 때, $\Gamma(\frac{1}{2}) = \sqrt{\pi}$를 많이 이용하는데 이 값이 어떻게 도출되는 지 다루어 보겠습니다. 이 값은 치환 적분과 극좌표를 이용하여 구할 수 있습니다.

• $$\Gamma(\alpha) = \int_{0}^{\infty} t^{\alpha - 1} e^{-t} dt$$
• $$\Gamma(\frac{1}{2}) = \int_{0}^{\infty} t^{-\frac{1}{2}} e^{-t}dt$$

• 이 때, $x = \sqrt{t}$로 치환하면, $dx = \frac{1}{2}t^{-\frac{1}{2}} dt$가 됩니다.

• $$\Gamma(\frac{1}{2}) = 2 \int_{0}^{\infty} e^{-x^{2}} dx$$
• $$\Gamma(\frac{1}{2})^{2} = 4 \int_{0}^{\infty} e^{-x^{2}} dx \int_{0}^{\infty} e^{-y^{2}} dy$$
• $$= 4\int_{0}^{\infty} \Bigl(\int_{0}^{\infty} e^{-x^{2}} \Bigr)dx \ e^{-y^{2}} dy$$
• $$= 4\int_{0}^{\infty}\int_{0}^{\infty} e^{-x^{2}}e^{-y^{2}}dx \ dy$$
• $$= 4\int_{0}^{\infty}\int_{0}^{\infty} e^{-(x^{2} + y^{2})} dx \ dy$$

• 위 식에서 사용된 $x, y$를 극좌표가 사용되는 공간으로 가져와서 변환해 보도록 하겠습니다.

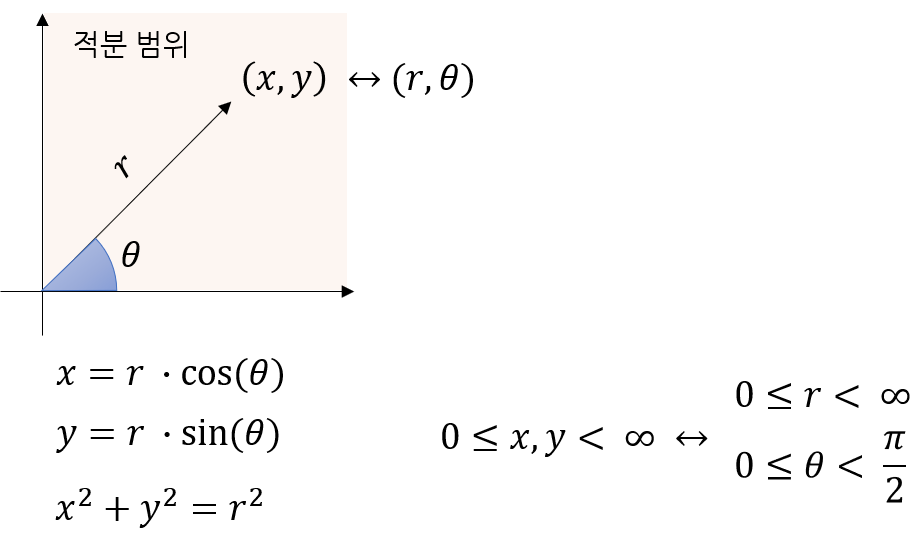
• 위 그림과 같이 $x, y$는 $r, \theta$ 로 변환될 수 있고 범위도 변하게 되어 다음 식과 같아 집니다.

• $$\int\int\ f(x, y)\ dx\ dy = \int\int\ f(r\cos(\theta), r\sin(\theta))\ r\ dr \ d\theta$$

• 위 식에서 $dx\ dy$ 가 $r\ dr \ d\theta$ 로 변환된 이유는 다음과 같습니다.

• $$x = r\cos\theta$$
• $$y = r\sin\theta$$

• 위 식에서 $r, \theta$를 이용하여 야코비안으로 변수 변환하면 다음과 같이 전개됩니다.

• $$\begin{vmatrix} \frac{\partial(x, y)}{\partial(r, \theta)} \end{vmatrix}$$
• $$= \begin{vmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \end{vmatrix}$$
• $$= r\cos^{2}\theta + r\sin^{2}\theta = r$$
• 따라서 나머지 식을 전개하면 다음과 같이 정리됩니다.

• $$\Gamma(\frac{1}{2})^{2} = 4 \int_{0}^{\frac{\pi}{2}} \int_{0}^{\infty} e^{-r^{2}}r \ dr \ d\theta$$

• 여기서 $\int_{0}^{\infty} e^{-r^{2}}r \ dr$ 부분과 $\theta$는 관련이 전혀 없으므로 $\theta$ 관련 적분 밖으로 나올 수 있습니다.

• $$= 4 \int_{0}^{\infty} \Biggl( \int_{0}^{\frac{\pi}{2}}1 \ d\theta \Biggr) e^{-r^{2}}r \ dr$$
• $$= 4 \cdot \frac{\pi}{2} \int_{0}^{\infty} re^{-r^{2}}\ dr\ d\theta$$

• 치환 적분을 통해 식을 전개 합니다. $u = -r^{2}, du = -2rdr$로 치환합니다. 그러면 다음 식과 같이 됩니다.

• $$= 4 \cdot \frac{\pi}{2} \int_{0}^{\infty} re^{-u}\ \frac{-1}{2r}du$$
• $$= 4 \cdot \frac{\pi}{2} \cdot (-\frac{1}{2}) \int_{0}^{\infty} e^{-u} du$$
• $$= 4 \cdot \frac{\pi}{2} \cdot (-\frac{1}{2}) [ e^{-u} ]_{0}^{\infty}$$
• $$= \pi$$

• 따라서 양변에 루트를 적용하면 최종적으로 다음과 같이 정리 됩니다.

• $$\Gamma(\frac{1}{2}) = \sqrt{\pi}$$

감마 분포와 지수 분포

• 앞에서 살펴본 감마 함수를 이용하여 감마 분포에 대하여 알아보도록 하겠습니다. 먼저 감마분포의 정의는 다음과 같습니다.
• 연속 확률 변수 $X$의 확률 밀도 함수가 아래와 같이 주어질 때, $X$는 모수 $\alpha, \beta$를 가지는 감마 분포를 따릅니다.

• $$f(x; \alpha, \beta) = \begin{cases} \frac{1}{\beta^{\alpha}\Gamma(\alpha)}x^{\alpha - 1}e^{-\frac{x}{\beta}}, & x > 0 \\ 0, & \text{else} \ x \end{cases}$$
• $$(\alpha > 0, \beta > 0)$$

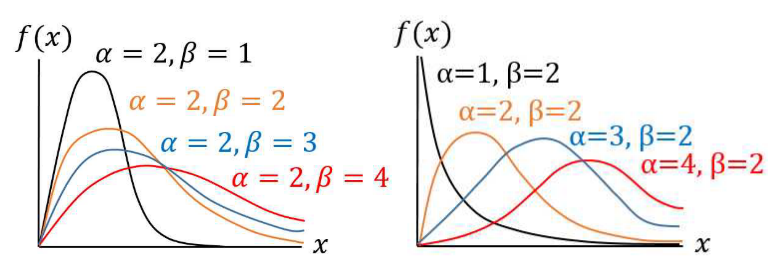
• 감마 분포의 분포 곡선은 위 그림과 같고 그 모양은 파라미터인 $\alpha, \beta$에 따라 달라지게 됩니다.
• 이 때, $\alpha$는 분포의 모양을 결정하므로 shape parameter 라고 하며 $\beta$는 크기를 결정하기 때문에 scale parameter 라고 합니다.
• 왼쪽 그림에서는 $\alpha$를 고정한 상태에서 $\beta$를 변경하여 가로 세로의 비율이 조정된 형태를 관찰할 수 있습니다.
• 오른쪽 그림에서는 $\beta$를 고정한 상태에서 $\alpha$를 변경하여 그래프의 모양이 변경되는 것을 관찰할 수 있습니다.

• 지수 분포는 감마 분포의 shape parameter $\alpha = 1$인 특수한 경우로 정의됩니다.
• 따라서 감마 분포로 부터 도출된 지수 분포의 정의는 다음과 같습니다.

• $$f(x; \beta) = \begin{cases} \frac{1}{\beta}e^{-\frac{x}{\beta}}, & x > 0 \\ 0 & \text{else} \ x \end{cases}$$
• $$(\beta > 0)$$

• 위 식에서 지수 분포는 모수 $\beta$에 따라 분포가 결정됩니다.

• 감마 분포에 대해서 간략하게 알아보았는데, 감마 함수에서 어떻게 감마 분포가 도출 되는 지 알아보겠습니다. 앞에서 소개한 것과 같이 감마 분포는 감마 함수 식에서 도출되었습니다.

• $$\Gamma(\alpha) = \int_{0}^{\infty} t^{\alpha -1}e^{-t} dt$$

• 감마 함수의 양변에 $\Gamma(\alpha)$로 나누겠습니다.

• $$1 = \int_{0}^{\infty} \frac{1}{\Gamma(\alpha)}t^{\alpha-1}e^{-t}dt$$

• 양수 $\beta$에 대하여 $t = \frac{x}{\beta}$ 라고 하면 $dt = \frac{1}{\beta}dx$ 가 됩니다.
• 앞에서 전개한 식에 $t = \frac{x}{\beta}$과 $dt = \frac{1}{\beta}dx$를 대입해 보겠습니다.

• $$1 = \int_{0}^{infty} \frac{1}{\Gamma(\alpha)}t^{\alpha-1}e^{-t}\ dt = \int_{0}^{\infty}\frac{1}{\Gamma(\alpha)} (\frac{x}{\beta})^{\alpha-1}e^{-\frac{x}{\beta}}\frac{1}{\beta} \ dx$$
• $$= \int_{0}^{\infty} \frac{1}{\beta^{\alpha}\Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}} \ dx = \int_{0}^{\infty} f(x; \alpha, \beta) \ dx$$

감마 분포의 평균과 분산

• 감마 분포의 평균과 분산은 다음과 같습니다.

• $$\mu = \alpha\beta$$
• $$\sigma^{2} = \alpha\beta^{2}$$

• 위 결과가 감마 분포와 감마 함수를 통해 어떻게 도출되는 지 알아보도록 하겠습니다.
• 먼저 평균 $\mu = E(X)$ 를 알아보도록 하겠습니다.

• $$\mu = E(X) = x\cdot f(x; \alpha, \beta) = \frac{1}{\beta^{\alpha}\Gamma(\alpha)} \int_{0}^{\infty} x^{\alpha}e^{-\frac{x}{\beta}} \ dx$$
• $$y = \frac{x}{\beta} \ \ \ \ \text{substitution : } \ \ x = \beta y, dx = \beta dy$$
• $$\mu = \frac{\beta}{\Gamma(\alpha)} \int_{0}^{\infty} e^{-y} \ dy = \frac{\beta}{\Gamma(\alpha)}\Gamma(\alpha + 1) = \alpha\beta$$
• $$\because \ \Gamma(\alpha) = \int_{0}^{\infty}t^{\alpha-1}e^{-t} \ dt, \Gamma(\alpha) = (\alpha-1)\Gamma(\alpha-1)$$

• 다음으로 분산 $\sigma^{2} = E(X^{2}) - E(X)^{2}$을 알아보도록 하겠습니다.

• $$E(X^{2}) = \frac{1}{\beta^{\alpha}\Gamma(\alpha)} \int_{0}^{\infty} x^{\alpha+1}e^{-\frac{x}{\beta}} \ dx = \frac{\beta^{2}}{\Gamma(\alpha)} \int_{0}^{\infty} y^{\alpha+1}e^{-y} \ dy$$
• $$\frac{\beta^{2}}{\Gamma(\alpha)}\Gamma(\alpha+2) = \frac{\beta^{2}}{\Gamma(\alpha)}\alpha(\alpha+1)\Gamma(\alpha) = \alpha(\alpha+1)\beta^{2}$$
• $$\sigma^{2} = E(X^{2}) - \mu^{2} = \alpha^{2}\beta^{2} + \alpha\beta^{2} - \alpha^{2}\beta^{2} = \alpha\beta^{2}$$

지수 분포의 평균과 분산

• 감마 분포의 평균과 분산을 통해 지수 분포의 평균과 분산을 구해보겠습니다. 지수 분포는 감마 분포에서 $\alpha = 1$인 케이스입니다.

• $$\mu = \beta$$
• $$\sigma^{2} = \beta^{2}$$

포아송 과정과의 관계

• 포아송 분포는 어떤 길이의 시간이나 공간에서 특정한 시간이 발생할 확률을 나타냅니다.
  • 주어진 시간간격/영역 동안 평균 $\mu = \lambda t$번 발생할 때, $x$번 발생할 확률

• $$p(x, \lambda t) = \frac{e^{\lambda t}(\lambda t)^{x}}{x!} \ \ \ \ (x = 0, 1, 2, ...)$$

• 포아송 분포를 응용하면 $t$ 시간 동안 하나의 사건도 발생하지 않을 확률을 구할 수 있습니다.

• $$p(0; \lambda t) = \frac{e^{\lambda t}(\lambda t)^{0}}{0!} = e^{-\lambda t}$$

• 이번에는 관점을 조금 바꾸어서 확률 변수 $x$를 첫번째 포아송 사건이 발생하기까지의 소요된 시간으로 보고 $f(x)$를 $x$의 확률밀도함수라고 생각하겠습니다.
• 그러면 첫번째 사건이 발생하기까지 걸린 시간이 $x$보다 클 확률 = $x$ 시간 내 포아송 사건이 1 건도 발생하지 않을 확률이 됩니다.

• $$P(X > x) = e^{\lambda x}$$

• 그러면 $X$의 누적 분포 함수에 대하여 알아보겠습니다.

• $$P(0 \le X \le x) = 1 - e^{\lambda x} = \int_{0}^{x} f(t) \ dt$$

• 위 식에서 $t$는 누적 분포 함수를 나타내기 위해 도입한 변수입니다. 여기서 $f(t)$를 구하기 위해서 $1 - e^{\lambda x}$를 미분하면 $f(x) = \lambda e^{\lambda x}$가 됩니다.

• 이 때, $\lambda = \frac{1}{\beta}$이면, $\frac{1}{\beta} e^{-\frac{x}{\beta}} = f(x;\beta)$로 지수 분포가 됩니다.
• 여기서 핵심은 포아송 분포에서 횟수를 생각하다가 관점을 바꾸어서 시간에 대하여 생각한 것이 지수 분포와 감마 분포가 되는 것입니다.

확률 분포 정리

• 포아송 분포와 지수 분포, 감마 분포의 관계는 이산형 확률 분포에서 이항 분포, 음이항 분포, 기하 분포 관계와 유사합니다.
• 베르누이 과정 : 1회 성공 확률이 $p$인 독립시행을 반복하여 시행
• 이항 분포 : n회 베르누이 시행 중 x번 성공할 확률
• 음이항 분포 : k번째 성공이 일어날 때 까지 x번 시행했을 확률
• 기하 분포 : 첫번째 성공이 일어날 때 까지 x번 시행했을 확률

• 포아송 과정 : 일정 시간 간격/영역에서 평균 $\mu$번 발생하는 사건의 발생 횟수의 확률은 시간 간격/영역의 크기에 비례
• 포아송 분포 : 어떤 사건이 일정 간격 동안 평균 $\mu = \lambda t$번 발생하였을 때, $x$번 발생할 확률
• 감마 분포 : 어떤 사건이 일정 간격 동안 발생 횟수의 평균이 $\frac{1}{\beta}$로 주어질 때, $\alpha$번 발생했을 시간(대기 시간)에 대한 확률 분포
• 지수 분포 : 어떤 사건이 첫번째 발생하기 까지 걸리는 시간에 대한 확률 분포

• 통계학 관련 글 목록