감마분포와 지수분포 (Gamma distribution and Exponential distribution) 의 적용
2020, Apr 15
- 먼저 이전 글들에서 배운 개념들인 포아송 분포와 지수 분포의 개념은 다음과 같습니다.
- 포아송 분포 : 어떤 사건이 주어진
시간 간격동안 평균 \(\lambda t\)번 발생할 때,발생 횟수에 대한 확률 분포를 뜻합니다. 여기서 \(\lambda\)는발생 횟수와 관련된 파라미터입니다. - 지수 분포 : 어떤 사건이
첫 번째 발생하기 까지시간에 대한 확률 분포를 뜻합니다. 이 때 확률 분포의 평균은 \(\beta = \frac{1}{\lambda}\)로 \(\lambda\)는시간과 관련된 파라미터 입니다. - 따라서
포아송 분포와지수 분포는 공통된 파라미터 \(\lambda\)로 연관되어 있습니다.
- 그리고 포아송 분포의 특징 중에는
포아송 분포의 건망성이라는 것이 있었습니다. 이것은 계속적으로 이어지는 시간 간격들에서 사건들은 서로독립적이라는 것입니다. - 포아송 분포에서는 시간 간격을 길게 가져가면 발생 횟수가 그에 비례해서 많아지고 반대로 시간 간격을 짧게 가져가면 발생 횟수가 그에 비례해서 작아져야 합니다. 이 조건을 만족하려면 각 발생 사건은 서로
독립적이어야 합니다. 즉, 조금 전에 어떤 사건이 발생했다고 하더라도 그것에 영향을 받으면 안되고 그 사건을 잊고 독립적으로 생각해야 하기 떄문에 포아송 분포의 건망성이라는 키워드로 특징을 정의합니다. - 앞의 사건과 앞으로 나올 사건이 독립적이라는 가정이 있기 때문에
지수 분포의 첫 번째 발생하기 까지 시간에 대한 확률을 같은 \(\lambda\) 파라미터를 이용하여 정의할 수 있습니다. 신뢰성 이론에서는 설비의 고장은포아송 과정을 따르게 되어 있으며 이러한 문제에지수 분포가 적용이 됩니다. 이 경우 \(\beta\)는 평균 고장 간격(mean time between failure)가 됩니다.
- 그러면
포아송 분포와지수 분포를 문제에 어떻게 적용할 수 있는지 살펴보겠습니다. 포아송 분포: 단위 당 평균 발생 사건건수가 알려져 있을 때, 단위 당 발생하는사건 수는 포아송 분포를 따릅니다.지수 분포: 어느 제품의 평균 수명이 \(\beta\)로 알려져 있을 때, 제품의 수명 \(X\)는 파라미터 \(\beta\)를 갖는 지수 분포를 따릅니다.
- 예1) 어느 가정에서 구입한 A 회사의 냉장고는 평균 10년 동안 고장이 없다고 합니다. 이 냉장고가 고장 날 때 까지의 시간이
지수 분포를 따를 때, 이 냉장고가 20년 이상 고장이 없을 확률과 5년 이내에 고장날 확률은 얼마인지 구해보겠습니다.
- 문제 조건에 따라 \(X\) 를 냉장고가 처음으로 고장 날 때 까지의 시간이라고 하면, \(X\)는 \(\mu = \beta = 10\)인 지수 분포를 가지게 됩니다.
- \[\text{Probability Density Function : } f(x; 10) = \frac{1}{10}e^{-\frac{1}{10}x} \ \ \ \ (x > 0)\]
- \[\text{No failure during 20 years : } P(X \ge 20) = \int_{20}^{\infty} f(x) dx = \int_{20}^{\infty} \frac{1}{10}e^{-\frac{1}{10}x} dx = [ -e^{-\frac{1}{10}x} ]_{20}^{\infty} = e^{-2} \approx 0.1353\]
- \[\text{failure under 5 years : } P(X \ge 5) = \int_{0}^{5} f(x) dx = \int_{0}^{5} \frac{1}{10}e^{-\frac{1}{10}x} dx = [ -e^{-\frac{1}{10}x}]_{0}^{5} = 1 - e^{-\frac{1}{2}} \approx 0.3935\]
- 예2) 어느 병원에서 환자가 도착하여 진료를 받기까지 기다리는 시간은 평균 30분이며 지수 분포를 따른다고 가정하겠습니다. 어떤 환자가 진료를 받기 까지 40분 이상 걸릴 확률과 이 환자가 기다릴 평균 시간과 분산을 구하보겠습니다.
- 환자가 기다리는 시간을 \(X\)라고 하면 \(X\)의 평균은 30이므로 \(X\)는 \(\mu = \beta = 30\)인 지수 분포를 갖습니다.
- \[\text{PDF : } f(x) = \frac{1}{30}e^{-\frac{1}{30}x}\]
- \[P(X > 40) = \int_{40}^{\infty} \frac{1}{30}e^{-\frac{1}{30}x} dx = e^{-\frac{4}{3}} = 0.2636\]
- \[\mu = E[X] = \beta = 30\]
- \[\sigma^{2} = \beta^{2} = 900\]
- 예3) 어떤 부품이 고장나기 까지 걸리는 시간을 나타내는 확률 변수를 \(T\)라고 할 때, \(T\)는 고장나기 까지 평균 시간이 \(\beta = 5\)인 지수 분포를 따른다고 가정하겠습니다. 이 부품 5개가 각각 다른 시스템에 설치되었다고 할 때, 8년이 지난 후 적어도 2개의 부품이 여전히 작동하고 있을 확률은 얼마일까요?
- 하나의 부품이 8년 이상 작동할 확률은 다음과 같습니다.
- \[P(T > 8) = \int_{8}^{\infty} \frac{1}{5}e^{-\frac{1}{5}t} dt = e^{-\frac{8}{5}} \approx 0.2\]
- 이 때, \(X\)가 8년이 지난 후 작동하고 있을 부품의 수를 나타내는 확률변수라고 하겠습니다. 그러면 이항분포를 이용하여 다음과 같이 구할 수 있습니다.
- \[P(X \ge 2) = \sum_{x = 2}^{5} b(x; 5, 0.2) = 1 - \sum_{0}^{1}b(x; 5, 0.2) \approx 1 - 0.7373 = 0.2627\]
지수 분포의 건망성(무기억성 : memoryless)
- 부품 수명이나 설비의 신뢰성 문제에 널리 사용되는 지수 분포는
건망성또는무기억성의 특징이 있습니다. - 어떤 부품의 수명이 지수 분포를 따른다고 할 때, 부품의 수명이 \(t\)시간 이상 될 확률 \(P(X \ge t)\)는 조건부 확률 \(P(X \ge t_{0} + t \vert X \ge t_{0})\)와 같습니다. 즉, 이 부품이 \(t_{0}\) 시간 동안 고장 없이 작동한 후 앞으로 \(t\) 시간 더 작동할 확률은 애초에 \(t\) 시간 이상 작동할 확률과 같습니다. 처음 \(t_{0}\) 시간 동안 작동에 따른 부품의 마모로 인한 영향은 발생하지 않는다는 조건입니다.
- 왜냐하면 앞에서 설명한 것과 같이
포아송 분포와지수 분포에 적용되는 사건의독립성때문입니다. - 일반적으로 기계부품 등 점진적으로 일어나는 마모로 인해 고장이 발생하는 경우 독립적이지 않을 수 있습니다. 따라서
감마 분포또는 이후 다른 글에서 다룰와이블 분포를 이용하여 신뢰성 문제를 접근하는 것이 타당하며 실제로와이블 분포를 많이 사용하고 있습니다. - 이 글에서는
감마 분포에 대하여 다루어 보겠습니다. 감마 분포는 어떤 사건이 \(\alpha\) 번 연속적으로 나왔을 때의 확률 분포를 나타내므로 지수 분포에 비해서는 상대적으로 신뢰성 문제를 다루기에 적합합니다.
- 예4) 전화 교환기에 전달되는 호출 신호는 분당 평균이 5회인 포아송 과정을 따른다고 가정하겠습니다. 1분 내에 2번의 호출 신호를 받을 확률을 구해보겠습니다.
- 2번의 호출 신호가 도착되기 까지의 소요된 시간을 \(X\) 라고 하면, 이는 2번의 포아송 사건이 발생되기 까지 소요된 시간으로 \(\alpha = 2, \beta = \frac{1}{5}\)인 감마 분포를 따르는 확률 변수이므로, 구하고자 하는 확률은 다음과 같습니다.
- \[P(X \le 1) = \int_{0}^{1} \frac{1}{\beta^{2}\Gamma(2)}x e^{-\frac{x}{\beta}} dx = 25 \int_{0}^{1}x e^{-5x} = 1 - e^{-5}(1 + 5) = 0.96\]
- 예5) 어떤 의학 실험에서는 독극물이 생존 시간에 미치는 영향을 살펴보기 위하여 쥐를 이용하여 용량 반응 검사를 수행한다고 가정하겠습니다. 연구에 의하면 일정량의 독극물에 대한 생존 시간은 \(\alpha = 5, \beta = 10\)인 감마 분포를 따른다고 할 때, 어떤 쥐에 독극물을 주입했을 때, 60주 이상 생존하지 못할 확률은 얼마인지 구해보겠습니다.
- 이 문제에서 \(X\)를 생존 시간이라고 하면 다음 식을 구하는 문제가 됩니다.
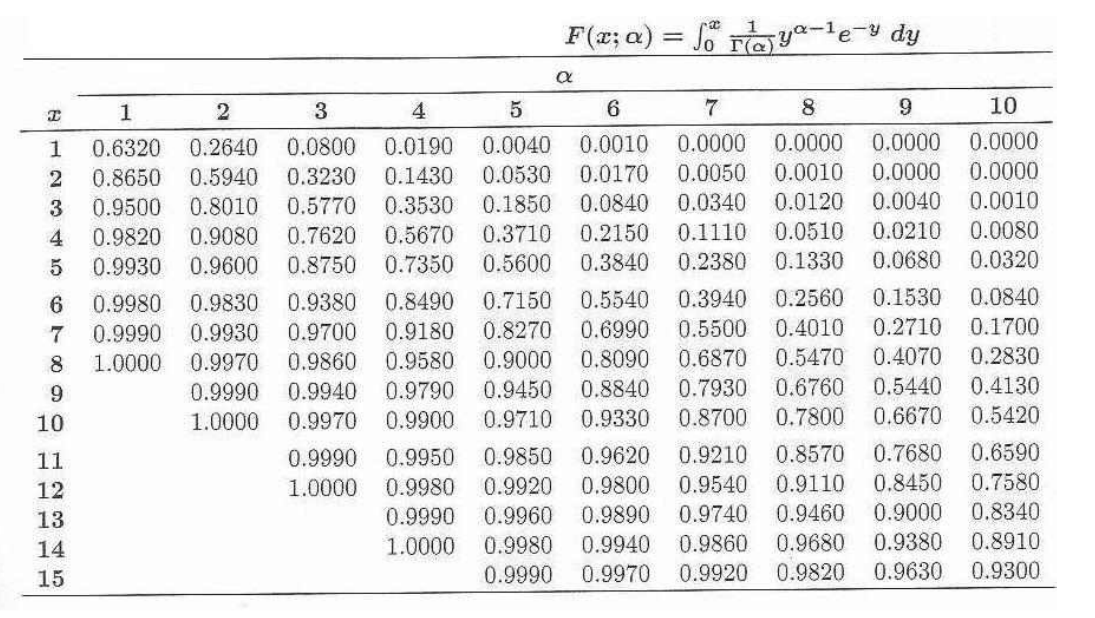
- \[P(X \le 60) = \frac{1}{\beta^{5}} \int_{0}^{60} \frac{x^{\alpha-1}e^{-\frac{x}{\beta}}}{\Gamma(\alpha)}\ dx\]
- 식의 계산이 복잡하므로 아래
불완전 감마함수 표를 이용하여 값을 구하겠습니다. 물론 컴퓨터를 이용하여 구하면 위 식을 그대로 이용하시면 됩니다.
- \[y = \frac{x}{\beta} \ \to \ x = \beta y \ \therefore \ dx = \beta dy\]