
분산과 공분산 (variance and covariance)
2019, Feb 07
- 참조 : Probability & Statistics for Engineers & Scientists. 9th Edition.(Walpole 저. PEARSON)
- 참조 : 수리통계학 (김수택 저. 자유 아카데미)
- 이번 글에서는
분산과공분산에 대하여 알아보도록 하겠습니다.
분산에 대하여
- 확률변수 \(X\)의 분산 (variance) 또는 \(X\)의 확률분포의 분산은 \(g(X) = (X - \mu)\)의 평균으로 나타내고 \(Var(X)\) 또는 \(\sigma^{2}_{X}\), \(\sigma^{2}\)으로 표시합니다.
- 이 때, \(X - \mu\)를 관측값의 평균으로부터의 편차(devication) 이라고 합니다.
- 이 내용을 정리하여 이산형 자료와 연속형 자료에서의 분산에 대한 정의는 다음과 같이 표현할 수 있습니다.

- 다음 예제를 통하여 분산의 정의를 살펴보겠습니다.
- A, B 두 회사에서 사용된 자동차의 수를 확률변수 \(X\)라고 하겠습니다. 이 때, 각 확률분포의 분산을 비교해 보겠습니다.

- ① A 회사의 경우
- \(\mu_{A} = E(X) = (1)(0.3) + (2)(0.4) + (3)(0.3) = 2\)
- \(\sigma^{2}_{A} = \sum_{x=1}^{3}(x-2)^{2}f(x) = (1-2)^{2}(0.3) + (2-2)^{2}(0.4) + (3-2)^{2}(0.3) = 0.5\)
- ② B 회사의 경우
- \(\mu_{B} = E(X) = (0)(0.2) + (1)(0.1) + (2)(0.3) + (3)(0.3) + (4)(0.2) = 2\)
- \(\sigma^{2}_{B} = \sum_{x=1}^{3}(x-2)^{2}f(x) = (0-2)^{2}(0.2) + (1-2)^{2}(0.1) + (2-2)^{2}(0.3) + (3-2)^{2}(0.3) + (4-2)^{2}(0.1)= 1.6\)
- 위 식과 같은 결과로 \(B\) 회사의 분산이 \(A\)회사의 분산보다 더 큰 것을 알 수 있습니다.
- 분산을 구할 때 다른 방법으로도 구할 수 있습니다.
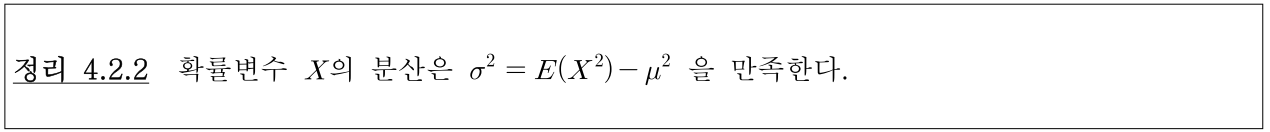
- 아래는 이산형 데이터에서의 분산을 구하는 방법입니다.
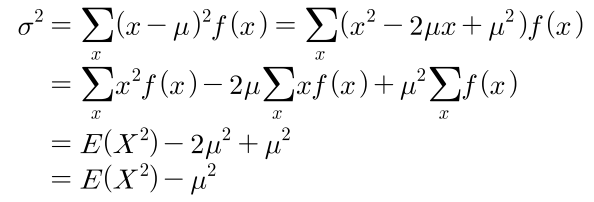
- 아래는 연속형 데이터에서의 분산을 구하는 방법입니다.
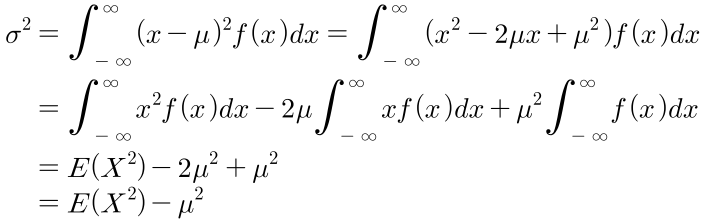
- 다음 예제를 살펴보겠습니다. 3개의 부품을 추출하여 검사하였을 때, 결함이 있는 부품의 수를 \(X\)라고 하고, 확률분포가 다음과 같을 때, 분산을 구해보겠습니다/

- \(\mu : (0)(0.51) + (1)(0.38) + (2)(0.1) + (3)(0.01) = 0.61\)
- \(E(X^{2}) = (0)(0.51) + (1)(0.38) + (4)(0.1) + (9)(0.01) = 0.87\)
- \(\sigma^{2} = E(X^{2}) - \mu^{2} = 0.87 - (0.61)^{2} = 0.4979\)
- 다음 예제도 살펴보겠습니다.
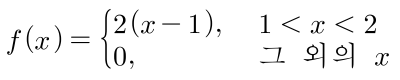
- \(\mu = E(X) = \int_{1}^{2} 2(x-1) \cdot x dx = 2\int_{1}^{2}x(x-1)dx = \frac{5}{3}\)
- \(E(X^{2}) = 2\int_{1}^{2}x^{2}(x-1) dx = \frac{17}{6}\)
- \(\sigma^{2} = \frac{17}{6} - (\frac{5}{3})^{2} = \frac{1}{18}\)

- 다음 예제를 살펴보겠습니다.


공분산에 대하여
- 공분산은 기존의 \(X\)의 분산 \(Var(X) = E((X-\mu)^{2})\)에서 확률 변수 \(X\)만을 사용하는 것이 아니라 서로 다른 확률 변수 \(X, Y\)를 사용하여 표현한다고 볼 수 있습니다.

- 이 때, \(X\)의 값이 클 때, \(Y\)의 값이 크고, \(X\)의 값이 작을 때, \(Y\)의 값이 작으면 \((X - \mu_{X})(Y - \mu_{Y})\)는 양의 값을 가집니다.
- 반면 \(X\)의 값이 클 때, \(Y\)의 값이 작거나, \(X\)의 값이 작을 때, \(Y\)의 값이 크면 \((X - \mu_{X})(Y - \mu_{Y})\)는 음의 값을 가집니다.
- 만약 \(X, Y\)가 통계적으로 독립이면 공분산 = 0이 됩니다. (다만, 역은 성립하지는 않습니다. 즉, 독립이 아닌 경우에도 공분산이 0일 수 있습니다.)

- 이산 확률 변수의 경우 아래와 같고 연속 확률 변수의 경우 \(\sum\)을 \(\int\)로 변경하면 됩니다.
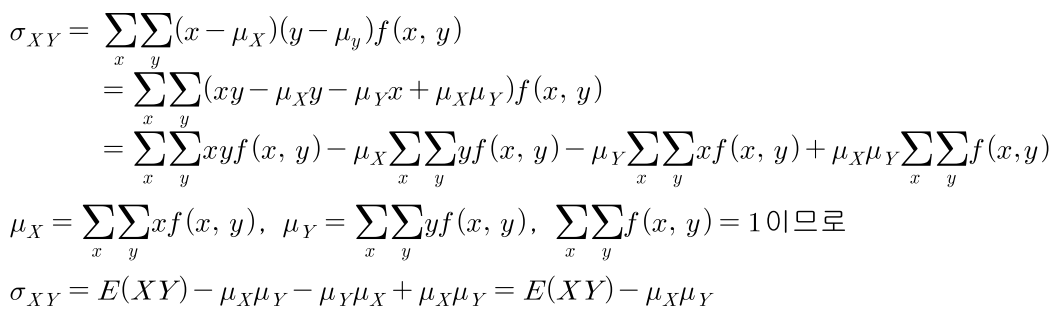
- 다음과 같이 이산확률분포의 예제를 살펴보겠습니다.

- 위 문제를 풀면 다음과 같습니다.

- 이번에는 연속확률분포의 예제를 살펴보겠습니다.


상관계수에 대하여
- 공분산 두 확률 변수 사이의 관련성을 나타내지만 \(\sigma_{XY}\)의 값은 \(X\)와 \(Y\)의 측정 단위에 따라 달라집니다. 상관계수 (correlation coefficient)는 측정 단위와 무관합니다. 즉
normalization하는 역할을 합니다..
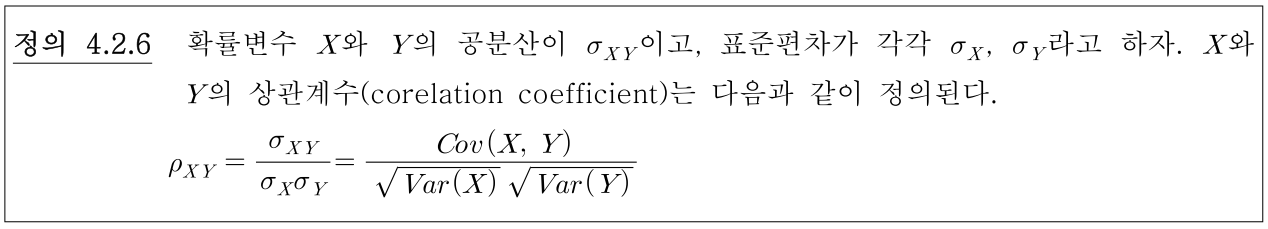
- 이 때, \(-1 \le \rho_{XY} \le 1\)을 만족하며 \(\rho_{XY}\)는 \(X, Y\)의 단위와 무관하게 -1 ~ 1의 범위를 가집니다.
- 만약 공분산 \(\sigma_{XY}\)가 0이면 상관계수값도 0을 가집니다.

- 위 문제를 풀면 다음과 같습니다.
