정상 회담 2

2019, Jun 04    

• https://www.acmicpc.net/problem/1670
• 이 문제 내용을 정리하면 원에 둘러 앉아있는 사람들을 짝을 짓고 짝을 지은 사람을 선으로 그었을 때, 그 선이 교차하지 않도록 하는 경우의 수의 총합입니다.
• 이 문제는 n명의 사람과 n+2 명의 사람이 있을 때 상태에 따라 점화식을 세울 수 있습니다. 따라서 dynamic programming 방법으로 문제를 해결할 수있습니다.

\(dp[i]\) : i 명의 사람이 원탁에 둘러 앉아 있을 때, 완벽하게 악수하는 경우의 수

[dp[i] = \sum_{j=0}^{i-2} \Biggl( dp[j] \times dp[i-(j+2)] \Biggr)]

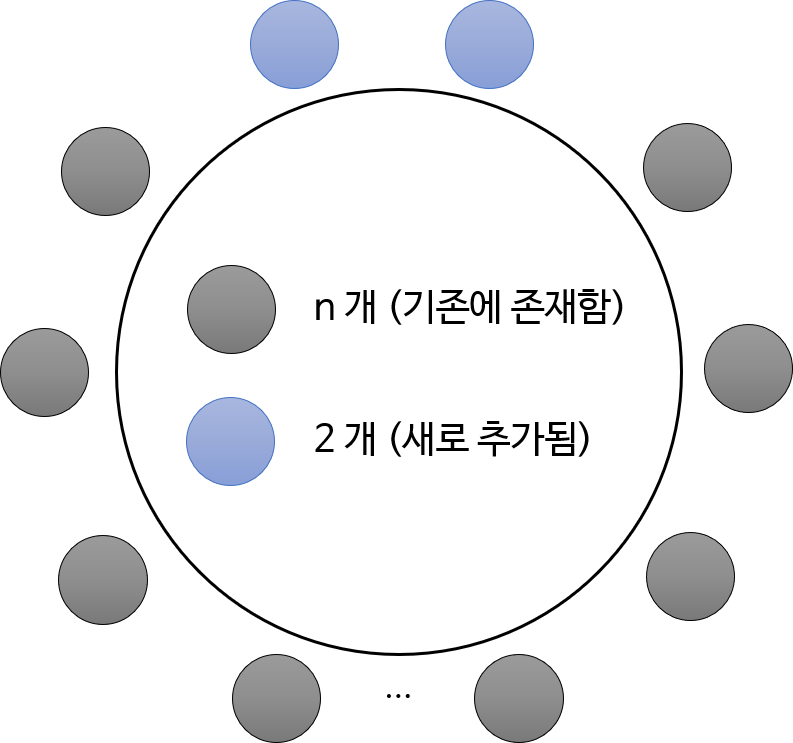
• 위 그림과 같이 기존에 n 명의 사람이 앉아 있었고 2명이 추가되었다고 생각해 보겠습니다.
• 그러면 기존의 n명의 사람이 완벽하게 악수하는 경우의 수는 \(dp[n]\)이 되고 위 그림 전체에서 완벽하게 악수하는 경우의 수는 \(dp[n+2]\)가 됩니다.

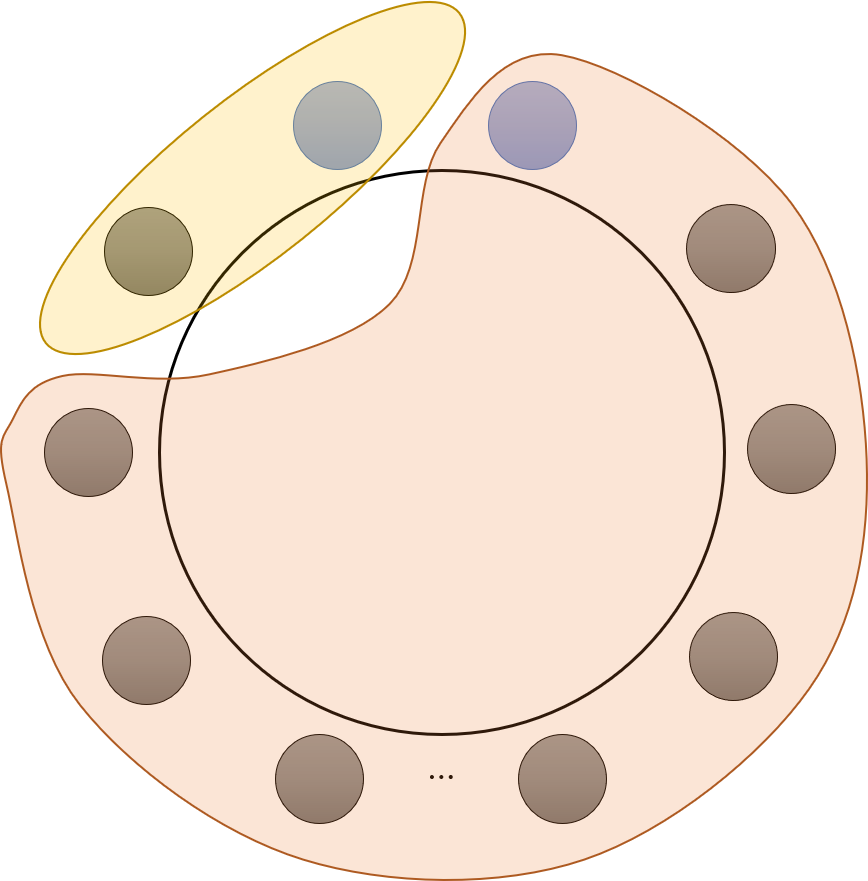
• 그러면 2명이 늘어남으로 인하여 새롭게 고려되어야 하는 점들을 생각해 보겠습니다.
• 새롭게 늘어난 점의 바로 옆의 점 2개의 집합과 나머지들 집합을 이용하여 경우의 수를 만들면 다음의 갯수 만큼 늘어납니다.

[dp[2] \times dp[n]]

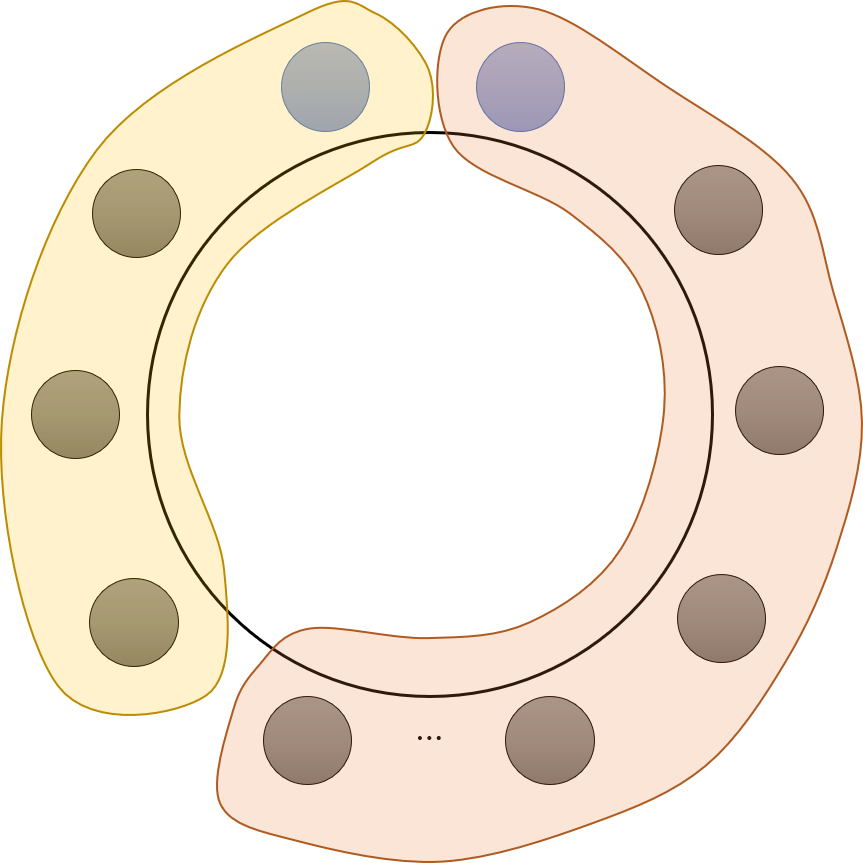
• 이번에는 2개의 집합에서 2명을 더 가져와서 4개의 집합을 만들어 보겠습니다. 항상 완벽하게 악수가 되는 경우만 고려하기 위하여 짝수의 갯수만큼 추가합니다. 이 경우 추가되는 경우의 수는 다음과 같습니다.

[dp[4] \times dp[n-2]]

• 이와 같은 방법으로 \(dp[n+2]\)는 다음 경우들이 모두 추가되어야 합니다.

[dp[2] \times dp[n]]

[dp[4] \times dp[n-2]]

[dp[6] \times dp[n-4]]

[\cdots]

[dp[n-4] \times dp[6]]

[dp[n-2] \times dp[4]]

[dp[n] \times dp[2]]

• 따라서 \(dp[n + 2]\)는 위 경우의 수를 모두 더한 것이므로 점화식을 다시 쓰면 아래와 같이 쓸 수 있습니다.

[dp[i] = \sum_{j=0}^{i-2} \Biggl( dp[j] \times dp[i-(j+2)] \Biggr)]

• 코드는 다음과 같습니다.