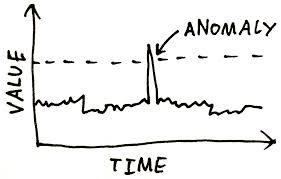
Anomaly Detection with Gaussian Distribution

이번 포스트에서는 이상 탐지 (Anomaly Detection)라는 문제에 대해 알려 드리고자합니다. 이 내용은 앤드류 응 교수님 강의 내용을 기반으로 만들어 졌습니다.

Anomaly Detection은 무엇일까?

Anomaly Detection은 Unsupervised Learning이지만 Supervised Learning의 성질을 가지고 있습니다.
- Anomaly Detection vs Supervised Learning 비교는 뒤에서 다루어 보겠습니다.
Anomaly Detection의 예
비행기 엔진 특성
- x1 = heat generated
- x2 = vibration intensity
- Dataset : ${x^{(1)}, x^{(2)}, ... , x^{(m)}}$
  - m 개의 생산된 비행기 엔지이 있다고 가정해 봅시다.
  - 아래 그림에서 파란색 점은 unlabeled로 학습된 데이터 입니다.
  - 빨간색 점은 테스트 데이터 입니다. 테스트 데이터는 새로 생산된 엔진으로 생각할 수 있습니다.
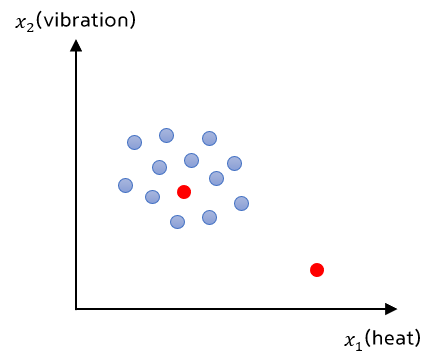
  - 위의 그림에서 직관적으로 이해해 보면 기존 데이터 무리에 있는 테스트 데이터는 normal 합니다.
  - 반면 기존 데이터 군집과 떨어져 있는 데이터의 경우 abnormal 하다고 생각해 볼 수 있습니다.
  - 확률적으로 나타내기 위해 학습한 모델을 P(x) 라고 가정해 보겠습니다.
    - 상수 $\epsilon$ 을 anomaly를 결정짓는 임계값이라고 하겠습니다.
    - 모델 $P(x_{test}) \lt \epsilon$ 이면 abnormal
    - 모델 $P(x_{test}) \ge \epsilon$ 이면 normal 이라고 할 수 있습니다.
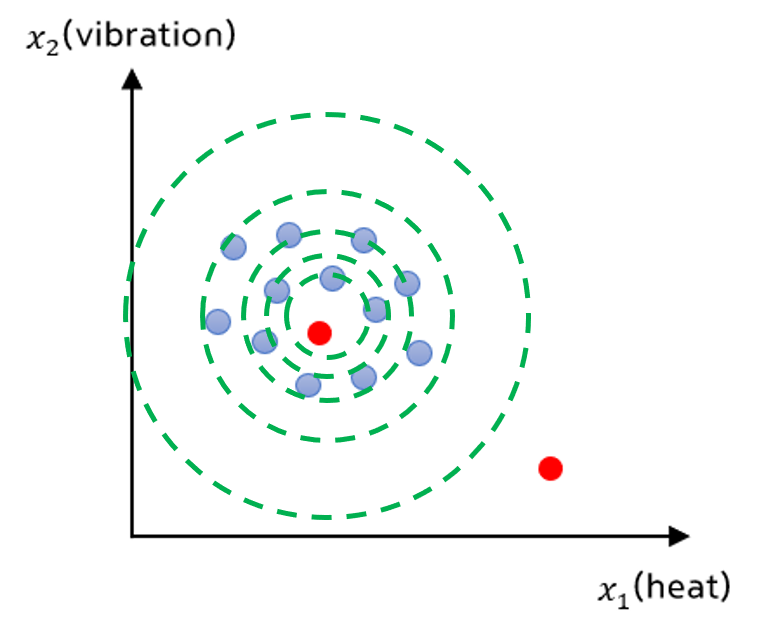
  - 데이터의 군집화 정도를 보았을 때, 중앙에 위치할 수록 normal일 확률은 높아지고 가장자리에 가까워질수록 abnormal에 가까워 집니다.
Fraud Detection (사기 감지)
- 데이터 $x^{(i)}$ = i 번째 사용자의 행동 특징 이라고 가정해 봅시다.
- 비행기 엔진 예제와 비슷하게 Model p(x)를 기존의 data를 통하여 구합니다.
- 새로운 사용자 즉, 새로운 데이터가 추가되었을 때, $p(x) \lt \epsilon$을 만족하는지 확인합니다.
Manufacturing (비행기 엔진과 유사)
데이터 센터에서의 컴퓨터 모니터링
- 데이터 $x^{(i)}$ = 컴퓨터 i의 특징이라고 하면
- x1 = 메모리 사용량, x2 = 디스크 접근수, x3 = CPU 부하, x4 = 네트워크 트래픽 등과같은 특성을 가질 수 있습니다.
만약 $\epsilon$이 너무 크다면 너무 많은 데이터가 $p(x) \lt \epsilon$을 만족해서 모델의 성능이 안좋아 질 수도 있습니다.
- 이럴 때에는, $\epsilon$의 크기를 줄여야 합니다.
Anomaly Detection 모델링을 할 때 주로 사용하는 것이 Gaussian Distribution 입니다. 그러면 Gaussian Distribution에 대하여 간략하게 알아보겠습니다.

Gaussian Distribution

Anomaly Detection 모델링을 하기 전에 근본이 되는 Gaussian Distribution에 대하여 알아보도록 하겠습니다.
데이터셋 x가 Gaussian Distribution을 따른다면 파라미터로 mean = $\mu$와 variance = $\sigma^{2}$을 가집니다.
- 기호로 표시하면 $x \sim N(\mu, \sigma^{2})$이 됩니다.
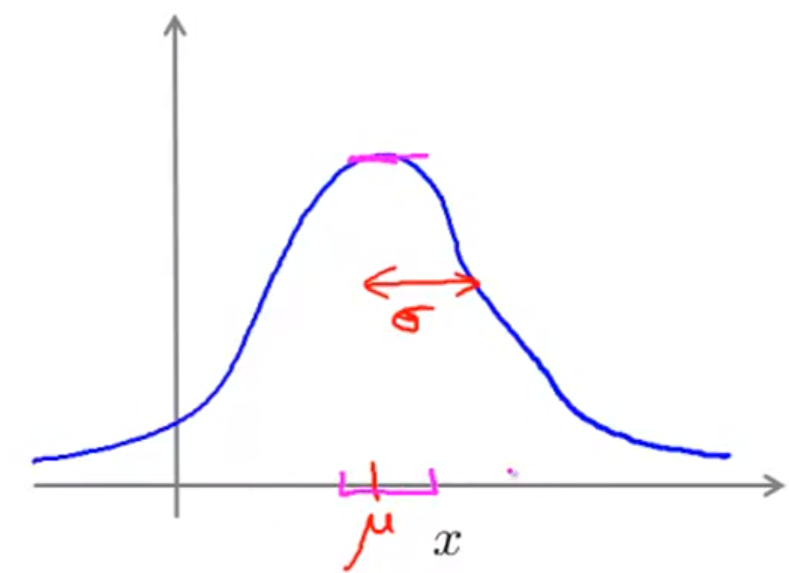
- Gaussian Curve는 기본적으로 종 모양의 곡선을 가집니다.
- 종 모양의 중간이 mean에 해당합니다.
- 곡선의 아랫 부분에 해당하는 면적이 확률이기 때문에 mean에서 멀어질수록 확률은 낮아지게 됩니다.
  - 아랫 부분의 면적은 확률이므로 면적의 넓이는 1이 됩니다.
- 일반적으로 $p(x; \mu, \sigma^{2})$로 표현합니다.
- 수식은 $p(x; \mu, \sigma^{2}) = \frac{1}{\sqrt{2\pi}\sigma} exp( -\frac{ (x-\mu)^{2} }{2\sigma^{2}} )$ 입니다.
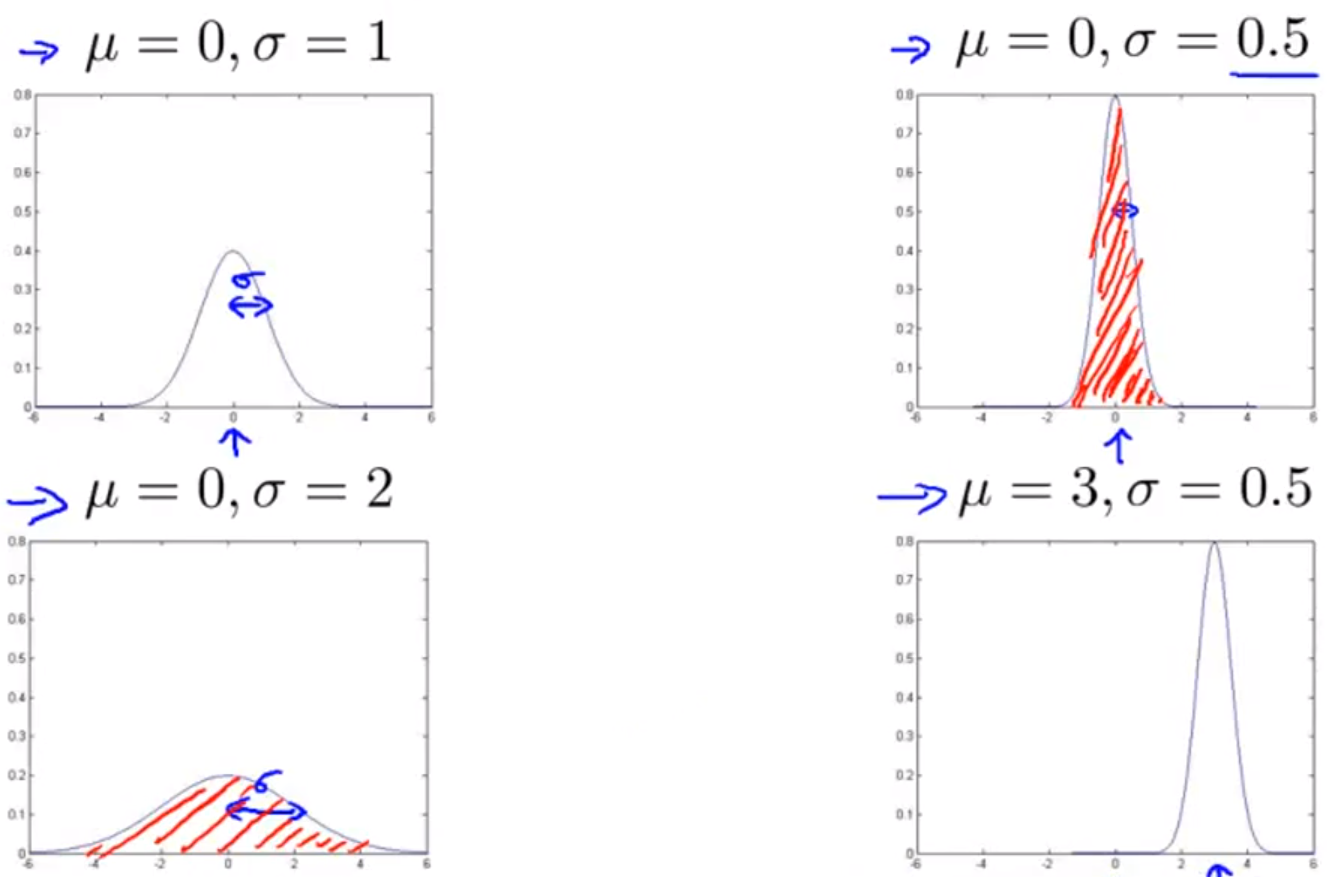
- 여기서 $\sigma$ 는 std(standard deviation)으로 종모양의 중심에서 얼마나 벌어져 있는지 너비에 대한 값입니다.
  - std가 클수록 너비가 커지므로 옆으로 퍼지게 되고 std가 작을수록 너비가 작아져 높이가 커지게 됩니다.
Gaussian Distribution 을 구할 때 기존의 데이터를 이용하여 Parameter extimation을 해야 합니다.
- 앞에서 설명한 바와 같이 $\mu, \sigma$ 두 개가 있습니다.
- DataSet = {x^{(1)}, x^{(2)}, … , x^{(m)} } 가 있을 때,
- mean = $\mu = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}$
- variance = $\sigma^{2} = \frac{1}{m} \sum_{i=1}^{m} (x^{(i)} -\mu)^{2}$
  - 이 때 표본 분산을 나누는 term은 정확하게는 m-1 입니다. 하지만 머신러닝과 같이 표본 데이터가 많은 경우에는 m으로 두고 계산해도 대동소이 합니다.
  - 왜 m-1로 나눠야 하는지는 다음 링크를 참조해 주세요.
    - https://gaussian37.github.io/ml-question-q6/

Anomaly Detection Algorithm

그러면 Anomaly Detection 알고리즘에 대하여 알아보도록 하겠습니다.

Dataset = $\{x^{(1)}, x^{(2)}, ..., x^{(m)} \}$ 이 있다고 가정해 봅시다.
각각의 $x^{(i)}$는 벡터 입니다. 따라서 벡터 내의 원소는 각각의 특징을 가지고 있습니다.
따라서 모델 $p(x) = p(x_{1})p(x_{2})...p(x_{m})$ 으로 나타낼 수 있습니다.
- 이 때, $x_{1} \sim N(\mu, \sigma^{2}), x_{2} \sim N(\mu, \sigma^{2}), ...$ 와 같이 나타낼 수 있습니다.
- 따라서 $p(x) = p(x_{1}; \mu_{1}, \sigma_{1}^{2})p(x_{2}; \mu_{2}, \sigma_{2}^{2})...p(x_{m}; \mu_{m}, \sigma_{m}^{2})$
- 위와 같은 형태로 확률의 곱이 유효하려면 $x_{i}$ 각각의 특성이 서로 독립적이어야 합니다.
- 실제 데이터의 경우 완전히 독립적인 feature를 가지기는 어려워 feature간 dependency가 있으나 위의 식은 효과가 있습니다.
p(x) 식을 좀 더 심플하게 정리해 보면 다음과 같습니다.
- 모델 $p(x) = p(x_{1}; \mu_{1}, \sigma_{1}^{2})p(x_{2}; \mu_{2}, \sigma_{2}^{2})...p(x_{m}; \mu_{m}, \sigma_{m}^{2}) = \Pi_{i=1}^{m} p(x_{i}, \mu_{i}, \sigma_{i}^{2})$

Anomaly Detection 알고리즘 순서

anomalous 한 특징을 찾을 수 있는 feature $x_{i}$를 선정합니다.
n개의 feature가 있을 때, $\mu_{1}, \mu_{2}, ..., \mu_{n}$ 과 $\sigma_{1}, \sigma_{2}, ..., \sigma_{n}$ 을 구합니다.
- 즉, $\mu$ 와 $\sigma$ 는 n개의 원소를 가지는 벡터 입니다.
- mean : $\mu_{j} = \frac{1}{m}\sum_{i=1}^{m}x_{j}^{(i)}$
- variance : $\sigma_{j}^{2} = \frac{1}{m}\sum_{i=1}^{m}(x_{j}^{(i)} - \mu_{j})^{2}$
새로운 데이터 x가 주어지면, 확률 p(x)를 계산합니다.
- 모델 $p(x) = \Pi_{j=1}^{n}p(x_{j}; \mu_{j}, \sigma_{j}) = \Pi_{j=1}^{n} \frac{1}{\sqrt{2\pi}\sigma_{j}}exp( -\frac{ (x_{j}-\mu_{j})^{2} }{2\sigma_{j}^{2}} )$ 입니다.
- 이 때 $\epsilon$ 값을 정하고 이 값보다 p(x)가 작으면 ($p(x) \lt \epsilon$) Anomaly로 판단합니다.
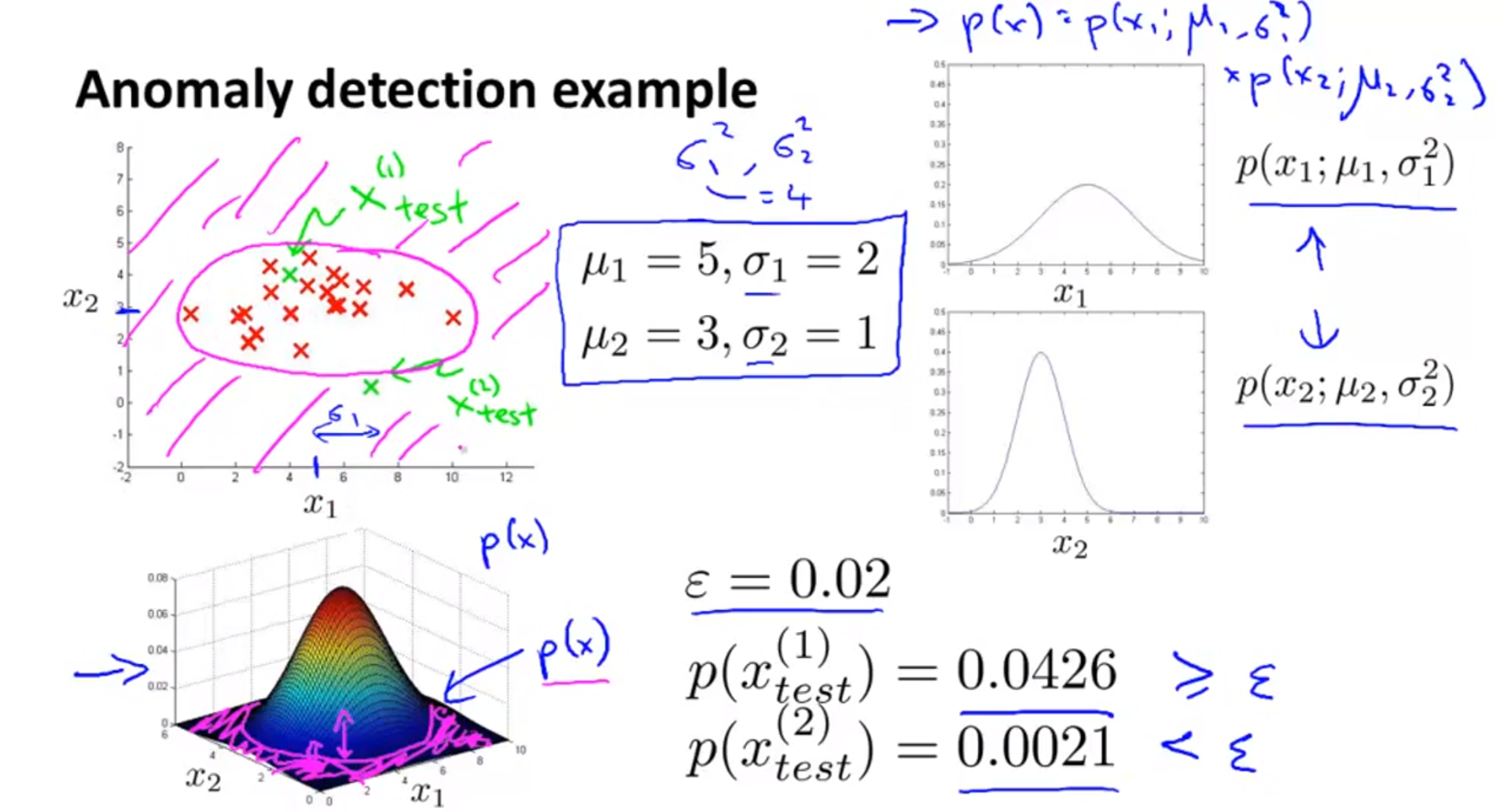
- 2d 그래프와 3d 그래프를 비교해서 보면, 2d에서 빨간색 점들이 모여있는 위치와 3d에서 높이가 높은 부분이 대응됩니다.
- 2d, 3d 그래프의 외곽지역 보란색 부분끼리 대응되고, 낮은 확률을 가집니다.
- 테스트 케이스 $x_{test}^{(1)}$ 의 확률은 0.0426이라고 했을 때, $\epsilon = 0.02$ 보다 크므로 normal 데이터 입니다.
  - 2d 그래프에서 $x_{1}$은 군집된 데이터 내부에 있습니다.
- 테스트 케이스 $x_{test}^{(2)}$ 의 확률은 0.0021이라고 하면 anomalous 한 데이터 입니다.
  - 2d 그래프에서 $x_{2}$은 군집된 데이터 외곽에 있습니다.

Multivariate Gaussian Distribution

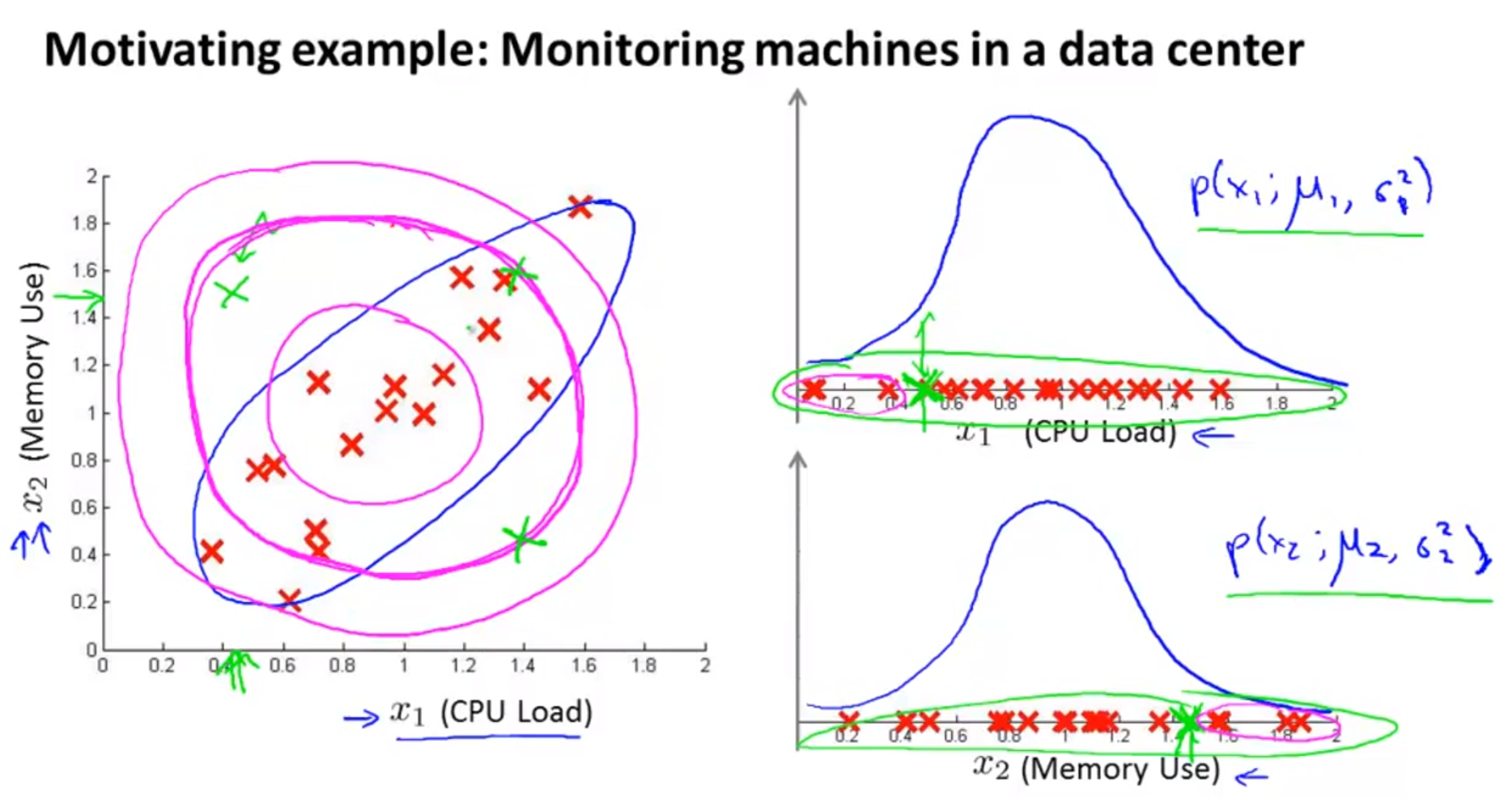
Anomaly Detection 알고리즘을 적용할 때, 여러가지 feature들이 발생할 수 있습니다.
- CPU Load 라는 feature $x_{1}$ 과 Memory Use 라는 feature $x_{2}$ 가 있습니다.
- feature 한 개의 관점에서 gaussian 분포를 적용하면 Anomolous 에 가까운 것이 2개의 feature 관점에서 보면 normal일 수 있습니다.
  - 연두색 포인트는 각각의 feature $x_{1}, x_{2}$ 에서 보았을 때는 분포의 끝에 가까워 보입니다.
  - 연두색 포인트 같은 점들이 2차원에서 보았을 때에는 normal한 점에 가깝다고 할 수 있습니다.
여러개의 feature들 즉, Multivariable을 가질 때의 gaussian 분포를 Multivariate Gaussian distribution 이라고 합니다.
- 즉, $x \in \mathbb{R}^{n}$ 에서 모델을 $p(x_{1}), p(x_{2}), ...$ 형태로 각각 만들지 않고
- p(x) 모델 하나에 모든 feature들을 나타냅니다.
Multivariate Gaussian distribution의 파라미터는 다음과 같습니다.
- 평균 $\mu \in \mathbb{R}^{n}$
- 공분산(covariance matrix) $\Sigma \in \mathbb{R}^{n x n}$
모델 $p(x;\mu,\Sigma) = \frac{1}{ (2\pi)^{\frac{n}{2}}\|\Sigma\|^{\frac{1}{2} }}exp(-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu))$
- feature의 갯수를 n차원, 데이터(instance)의 갯수를 m 이라고 하면
- $\|\Sigma\|^{\frac{1}{2}}$ : 실수(real number)
- $(x - \mu)^{T}$ : m x n 또는 n x m 차원
- $(x - \mu)$ : m x n 또는 n x m 차원
- $\Sigma^{-1}$ : n x n 차원
앞에서 배운 단일 feature에서의 gaussian 분포는 multivariate 버전의 식에서 feature가 1개일 때를 적용한 것입니다.
- 모델 $p(x; \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}exp(-\frac{(x-\mu)^{2}}{2\sigma^{2}})$
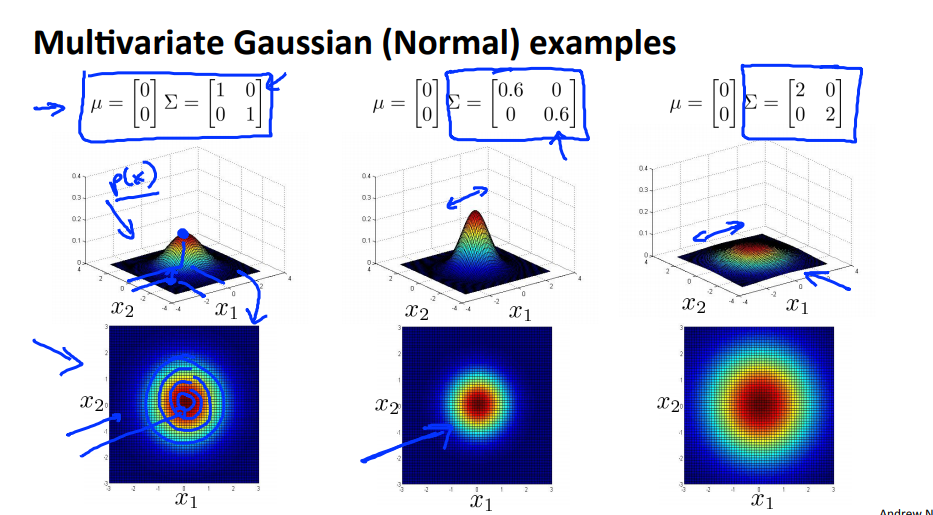
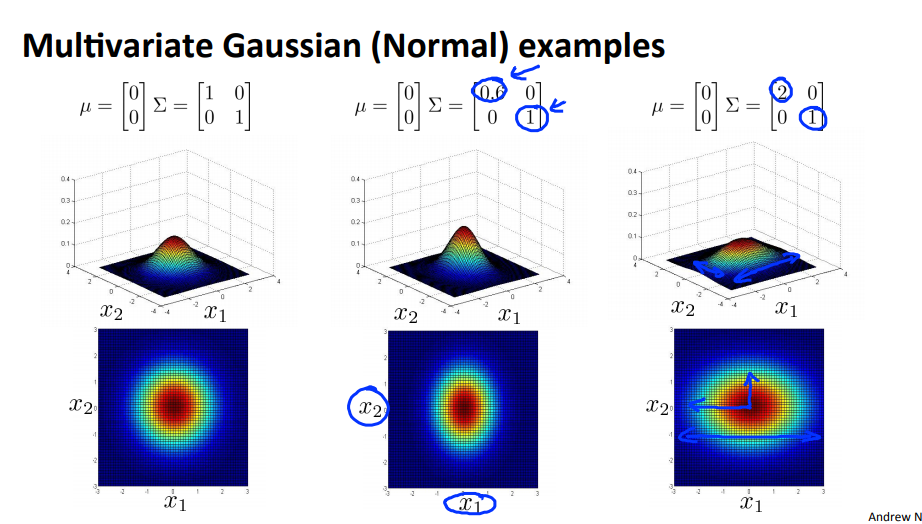
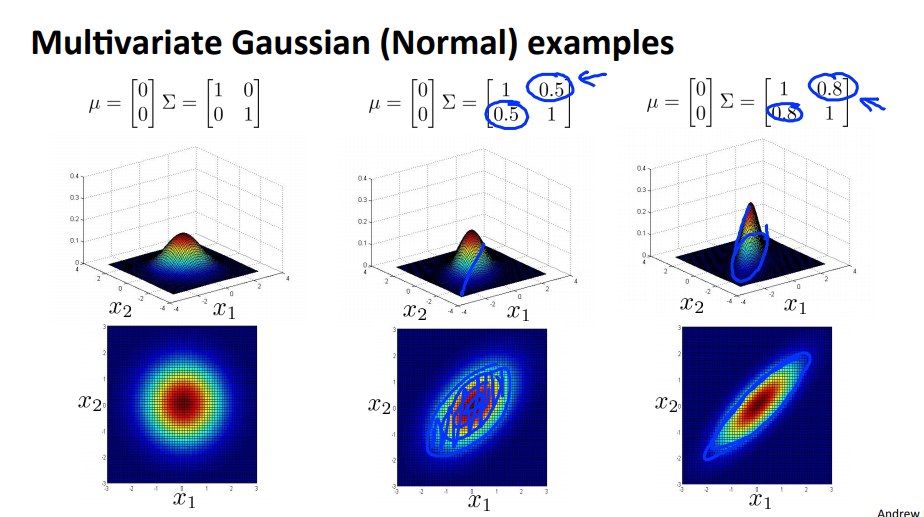
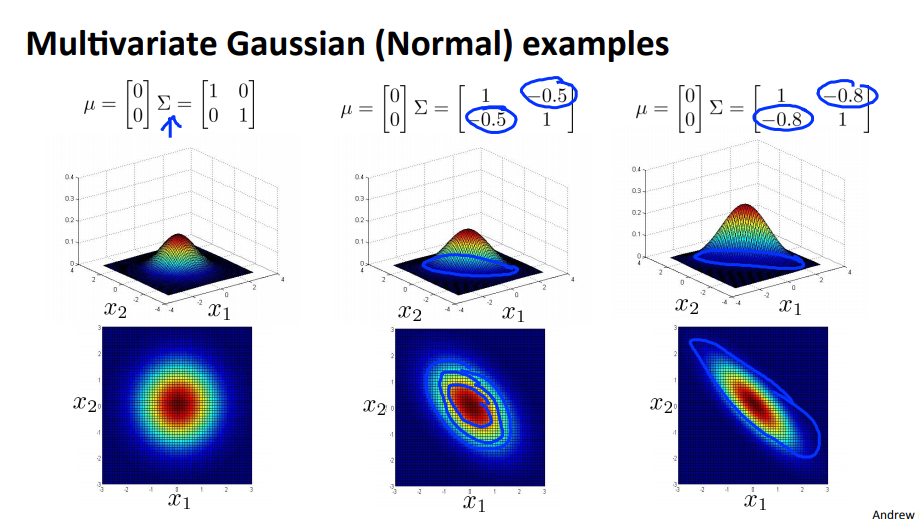
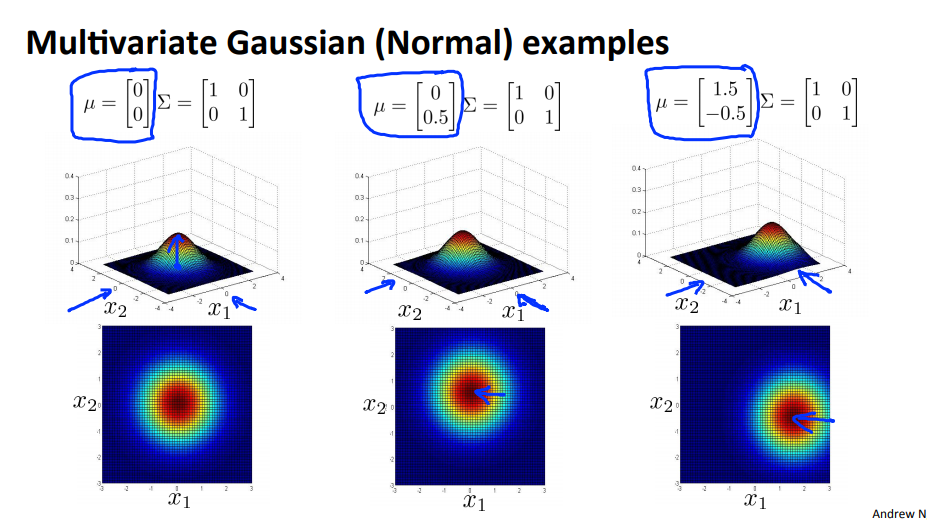
2개의 feature를 이용하여 gaussian distribution을 그려보겠습니다.
- 이 때 변경 가능한 부분은 $\mu$ 와 $\Sigma$ 입니다.
- 위에서 가장 왼쪽이 기본이라고 생각하고 비교해서 보면 분산 줄어들면 데이터가 모여서 뾰족한 형태가 되고 분산이 커지면 데이터가 펴져서 평평해 집니다.
- feature간의 분산의 크기가 다르다면(일반적으로), 타원 형태의 분포를 띄게 됩니다.
- 분산에서 diagonal 이외의 값이 추가 되면 전체적인 분포가 회전하게 됩니다. 양의 방향으로 회전한 결과 입니다.
- 분산에서 diagonal 이외의 값이 추가 되면 전체적인 분포가 회전하게 됩니다. 음의 방향으로 회전한 결과 입니다.
- 평균이 변하게 되면 분포의 중심이 변경되게 됩니다.

Anomaly detection using the Multivariate Gaussian Distribution

이제 Multivarirate Gaussian Distribution을 이용하여 Anomaly Detection을 하는 방법에 대하여 알아보도록 하겠습니다.

첫번째, Parameter fitting으로 training set가 $\{x^{(1)}, x^{(2)}, ..., \}$로 주어질 때,
- 평균 $\mu = \frac{1}{m}\sum_{i=1}^{m}x^{(i)}$
- 분산 $\Sigma = \frac{1}{m}\sum_{i=1}^{m}(x^{(i)} - \mu)(x^{(i)} - \mu)^{T}$
두번째, 새로운 데이터가 들어왔을 때,
- 학습된 Parameter : $\mu, \Sigma$을 $p(x;\mu,\Sigma) = \frac{1}{ (2\pi)^{\frac{n}{2}}\|\Sigma\|^{\frac{1}{2} }}exp(-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu))$ 에 적용시킵니다.
- 이 때, $p(x) \lt \epsilon$ 이면 anomalous 라고 판단합니다.
앞에서 배웠던 모델과 비교해 보면 $p(x) = p(x_{1}; \mu_{1}, \sigma_{1}^{2}) \times p(x_{2}; \mu_{2}, \sigma_{2}^{2}) \times ... \times p(x_{n}; \mu_{n}, \sigma_{n}^{2})$ 으로 식을 정의하였습니다.
이 식은 Multivariate Gaussian Distribution의 식 $p(x;\mu,\Sigma) = \frac{1}{ (2\pi)^{\frac{n}{2}}\|\Sigma\|^{\frac{1}{2} }}exp(-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu))$ 과 일치합니다.
- 단, covariance matrix에서 diagonal 이외의 성분은 반드시 0이어야 합니다.
기존의 모델과 Multivariate 모델을 비교해 보겠습니다.
- 기존 모델
  - 장점 :
    - 계산 비용이 작습니다.
    - 학습 데이터의 숫자가 작더라고 feature의 갯수를 크게 늘릴 수 있습니다.
  - 단점 :
    - feature들 간의 상관관계를 직접 찾아야 합니다.
- Multivariate 모델
  - 장점 :
    - feature들 간의 상관관계를 covariance matrix를 통해 자동으로 찾습니다.
  - 단점 :
    - covariance matrix를 구할 때 계산 비용이 $O(n^{2})$ 으로 비쌉니다.
    - 계산 과정 중 $\Sigma^{-1}$이 있으므로 반드시 역행렬이 존재해야 합니다.
    - 즉, feature들 간 independent 해야 합니다.
      - 예를 들어 x1 = x2, x5 = x3 + x4 와 같은 관계가 있으면 역행렬이 존재하지 않습니다.

Anomaly Detection Algorithm Evaludation

Anomaly Detection 알고리즘을 만들었다면 중요한 요소 중 하나인 evaluation 하는 방법에 대하여 알아보겠습니다. 다른 알고리즘들과 마찬가지로 평가하는 방법이 있어야 parameter tuning 이나 feature를 선택 하는 것이 쉬워집니다.

labeled 데이터를 가지고 있다고 가정해 보겠습니다.
- y = 0, normal
- y = 1, anomalous
Training set은 normal 데이터로 가정합니다.
- Training set : $x^{(1)}, x^{(2)}, ... , x^{(m)}$
Cross validation & Test set 에서는 anomalous 데이터를 추가합니다.
- Cross validation set : $$ (x_{cv}^{(1)}, y_{cv}^{(1)}), (x_{cv}^{(2)}, y_{cv}^{(2)}), …, (x_{cv}^{(m_{cv})}, y_{cv}^{(m_{cv})})
- Test set : $$ (x_{test}^{(1)}, y_{test}^{(1)}), (x_{test}^{(2)}, y_{test}^{(2)}), …, (x_{test}^{(m_{test})}, y_{test}^{(m_{test})})
예를 들어 다음과 같은 데이터 셋이 있다고 가정해 보겠습니다.
- 10,000개의 normal 데이터 (y = 0)
- 20개의 anomalous 데이터 (y = 1)
이 때 다음과 같이 training/validation/test 셋을 구성할 수 있습니다.
- Training set : 6,000개의 normal 데이터 (y = 0)
- CV : 2,000개의 normal 데이터 (y = 0) + 10개의 anomalous 데이터 (y = 1)
- Test : 2,000개의 normal 데이터 (y = 0) + 10개의 anomalous 데이터 (y = 1)
Algorithm evaluation 하는 방법은 다음 순서와 같습니다.
- 모델 p(x)를 training set $\{ x^{(1)}, x^{(2)}, ... , x^{(m)}$ 에 학습 시킵니다.
- cross validation/test example x 에서 아래와 같이 판단합니다.
  - 만약 $p(x) \lt \epsilon$ 이면 anomalous
  - 만약 $p(x) \gt \epsilon$ 이면 normal
- 판단한 결과를 evaluation 하는 방법에는 다음과 같은 방법이 있습니다.
  - True positive/False positive/False negative/True negative
  - Precision/Recall
  - F1-score
- 단순히 normal, anomalous 한 데이터를 classification 하는 방식으로 accuracy를 생각하면 anomalous한 데이터가 너무 작기 때문에 적합하지 않습니다.
  - 무조건 normal 이라고 해도 accuracy가 상당히 높게 나오기 때문입니다.
- evaluation 한 내용을 기반으로 파라미터 $\epsilon$을 최종적으로 학습할 수 있습니다.

Anomaly Detection Vs. Supervised Learning

지금까지 Anomaly Detection을 공부해 보았으면, binary classification을 하는 Supervised Learning과 유사하다고 느꼈을 것입니다. 그러면 Anomaly Detection VS Supervised Learning에 대하여 비교해 보도록 하겠습니다.

Anomaly Detection
- positive example (y = 1) 이 매우 작을 때 유용합니다.
  - positive example이 매우 작으므로 어떤 형태가 positive인지 예측하기가 어렵습니다.
  - 과거에 전혀 발생하지 않은 positive 케이스를 미래에 positive라고 예측이 필요할 때 유용합니다.
- 반면 negative example (y = 0)은 매우 많은 상태입니다.
- 사용하기 좋은 예제 : Fraud Detection, Manufacturing, Monitoring machines
Supervised Learning
- positive/negative example 둘 다 충분히 있는 상태일 때 좋습니다.
  - positive example이 충분히 많은 상태이기 때문에 미래에도 과거에 나왔던 example과 유사하게 positive가 나올 확률이 높습니다.
- 사용하기 좋은 예제 : Classification, Prediction

Anomaly Detection에서는 어떤 feature를 사용하는 것이 좋을까?

Anomaly Detection 알고리즘에 적용할 feature는 어떻게 선정 하면 좋을 지 알아보도록 하겠습니다.

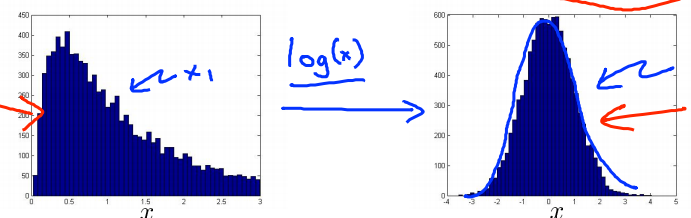
gaussian distribution이 되도록 feature를 수정합니다.
- feature의 분포를 보았을 때, 한번에 gaussian 분포를 따를 수도 있지만 그렇지 않는 경우도 많습니다.
- 위의 예제에서는 log(x) 함수를 적용하였을 때, 좀 더 gaussian 분포에 가까워 지는 것을 볼 수 있습니다.
  - gaussian 분포를 만들면 Anomaly Detection 알고리즘을 적용하기에 좀 더 적합해 집니다.
  - 다른 방법으로, $log(x), \sqrt{x}, \sqrt[3]{x}, ...$ 을 이용하여 gaussian 분포에 적합하도록 만들 수 있습니다.
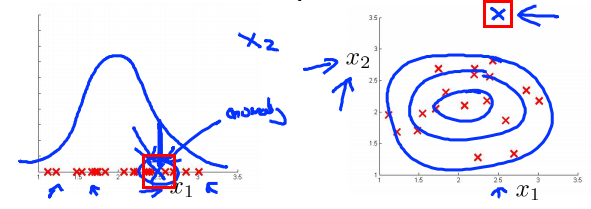
의미 있는 feautre를 추가했을 때, error를 줄일 수 있습니다.
- 위의 예제에서 1-dimension 상태 즉, $x_{1}$ feature 만으로는 Anomalous한 상태를 검출하지 못하는 경우가 발생 할 수 있습니다.
  - 이 때, $x_{2}$ feature를 추가하면 표현력이 더 증가하여 Anomalous한 상태를 확인할 수도 있습니다.
어떤 현상이 발생하였을 때, feature의 값이 비이상적으로 커지거나, 작아지도록 만들면 검출하기 쉬워집니다.
- 예를 들어, 데이터 센터에서 컴퓨터 상태를 모니터링 한다고 하고 x = CPU load 이고 y = network traffic 이라고 가정하겠습니다.
- 이 때, feature로 x, y를 사용하는 것 보다 z = (CPU load) / (network traffic) = x/y 를 사용하는 편이 나을 수 있습니다.
  - 어떤 컴퓨터의 CPU load가 비이상적으로 올라가면 network traffic은 작아지므로 z라는 feature는 x, y 보다 더 큰 특징을 가지게 됩니다.

Anomaly Detection with sklearn

전체 코드

라이브러리를 불러옵니다.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

from scipy.io import loadmat
from sklearn.svm import OneClassSVM
from sklearn.covariance import EllipticEnvelope

import seaborn as sns
sns.set_style('white')

데이터를 불러와서 변수에 저장합니다.

# 데이터를 로드 합니다.
data1 = loadmat("resources/data1.mat")
# 로드한 데이터의 key 값을 확인합니다.
print(data1.keys())

# 데이터 중 실제 데이터에 해당하는 X 값을 변수에 저장합니다.
X = data1['X']

# X 값을 확인합니다.
X = data1['X']
print('X:', X.shape)

gaussian 분포에 맞춰 데이터를 학습합니다.

# gaussian 분포를 이용하여 Outlier를 검출하는 EllipticEnvelope 객체를 선언합니다.
clf = EllipticEnvelope()
# 학습 데이터 X를 이용하여 gaussian 분포를 학습합니다.
clf.fit(X)

outlier를 구합니다.

# Calculate the decision function and use threshold to determine outliers
# decision_function을 이용하여 Mahalanobis distances를 구합니다.
y_pred = clf.decision_function(X).ravel()
# outlier를 백분위에서 얼마나 낮은 값이하로 설정할지 임계값을 정합니다. 
# percentile은 0 ~ 100 사이로 입력해야 하며 outlier검출 목적상 작은 값이어야 합니다.
percentile = 2
# y_pred에서 percentile 에 해당하는 값(threshold)를 구합니다.
threshold = np.percentile(y_pred, percentile)
# threshold 값보다 작은 값들의 index를 구합니다.
outliers = y_pred < threshold

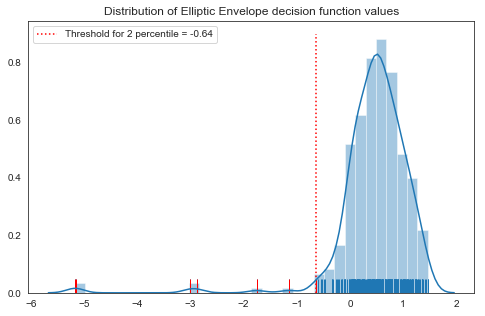
그래프를 그려 outlier를 구한 결과를 시각화 합니다.

# plot을 설정합니다.
fig, ax = plt.subplots(figsize=(8,5))

# decision function의 결과인 y_pred에 대한 분포를 그래프에 표시합니다.
sns.distplot(y_pred, rug = True, ax=ax)

# outliter를 그래프에 표시합니다.
sns.distplot(y_pred[outliers], rug=True, hist=False, kde=False, norm_hist=True, color='r', ax=ax)

ax.vlines(threshold, 0, 0.9, colors='r', linestyles='dotted',
           label='Threshold for {} percentile = {}'.format(percentile, np.round(threshold, 2)))

ax.set_title('Distribution of Elliptic Envelope decision function values');

ax.legend(loc='best')

Drawing