Clustering with K-Means Algorithm (Andrew Ng)

2019, Mar 24    

• 출처 : Andrew Ng 머신러닝

• 이번 글에서는 K-means 알고리즘을 이용한 Clustering 방법론에 대하여 알아보도록 하겠습니다.

• 먼저 Unsupervised Learning에 대한 개념을 알아본 뒤 K-means 알고리즘에 대하여 알아보도록 하겠습니다.

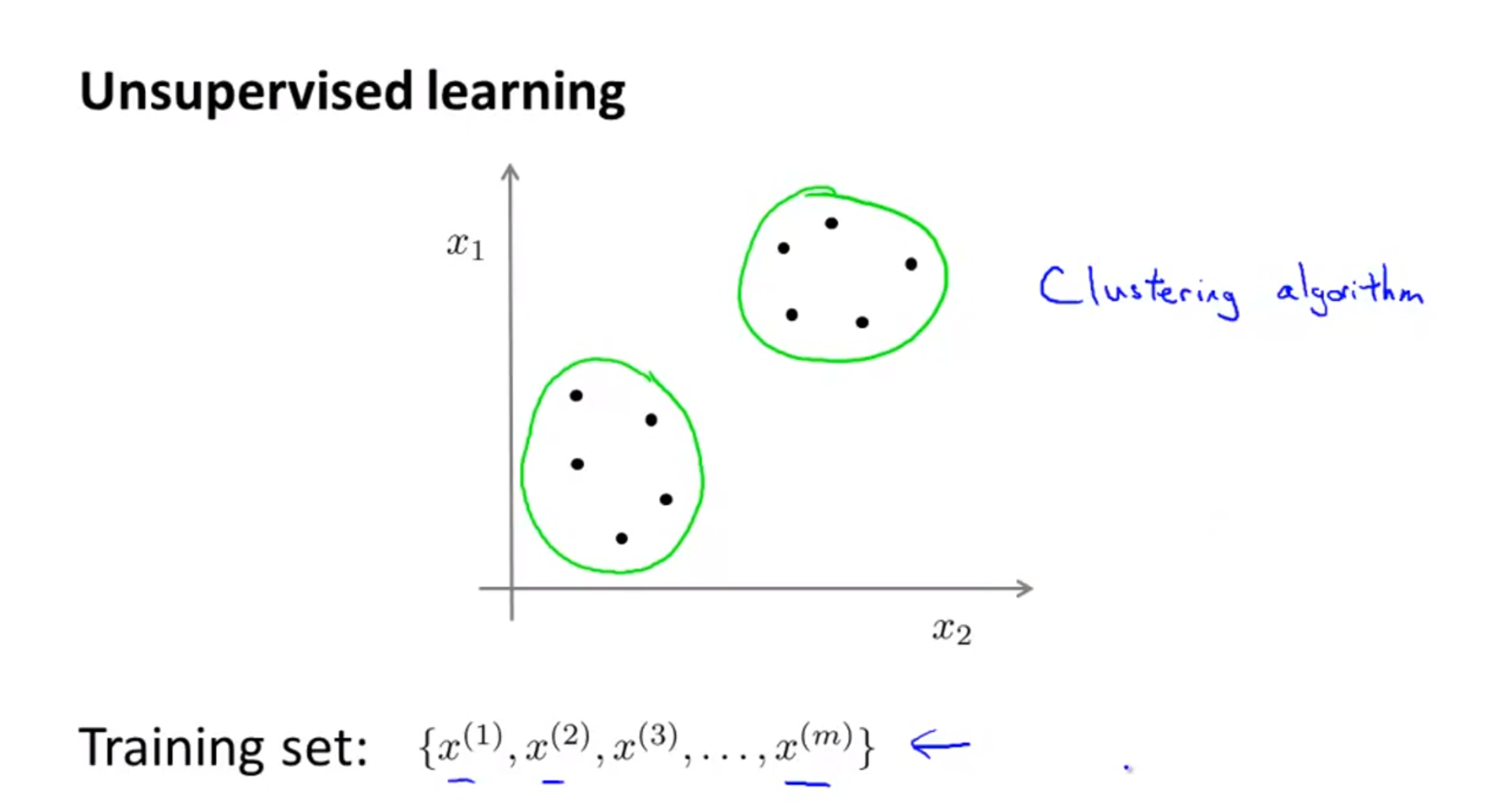
Unsupervised Learning

• 먼저 unsupervised learning에 대하여 간략하게 알아보도록 하겠습니다.
• unsupervised learning에서는 Training Set에 label 데이터가 없습니다.
  • 위 슬라이드의 training set을 보면 \(\{ x^{(1)}, x^{(2)}, ..., x^{(m)} \}\) 으로 \(y^{(i)}\) 에 해당하는 label이 없습니다.
• 여기서 우리가 할 일은 라벨이 없는 트레이닝 데이터를 알고리즘을 이용하여 데이터가 가지고 있는 어떤 구조를 찾는 것입니다.
  • 위 슬라이드에서 보면 두 개의 분리된 클러스터 구조를 가지고 있음을 알 수 있습니다.
  • 위와 같이 두 개의 클러스터를 만들어 내는 것을 Clustering algorithm 이라고 하며 unsupervised learning의 대표적인 알고리즘 입니다.

K-means Algorithm

• K means 알고리즘은 주어진 unlabeled 데이터셋에서 유사한 데이터 성격을 가지는 데이터 부분 집합들을 자동적으로 만들어 내는 데 사용됩니다.
  • K means 알고리즘은 가장 많이 그리고 자주 사용되는 clustering algorithm 중의 하나입니다.
• K-means 알고리즘에서는 2가지 스텝을 가집니다.
  • 첫번째, cluster assignment step 입니다. 이 단계에서는 K 개의 클러스터를 할당하는 작업을 합니다.
  • 두번째, move centroid step 입니다. 이 단계에서는 각 클러스터의 중심을 이동합니다.

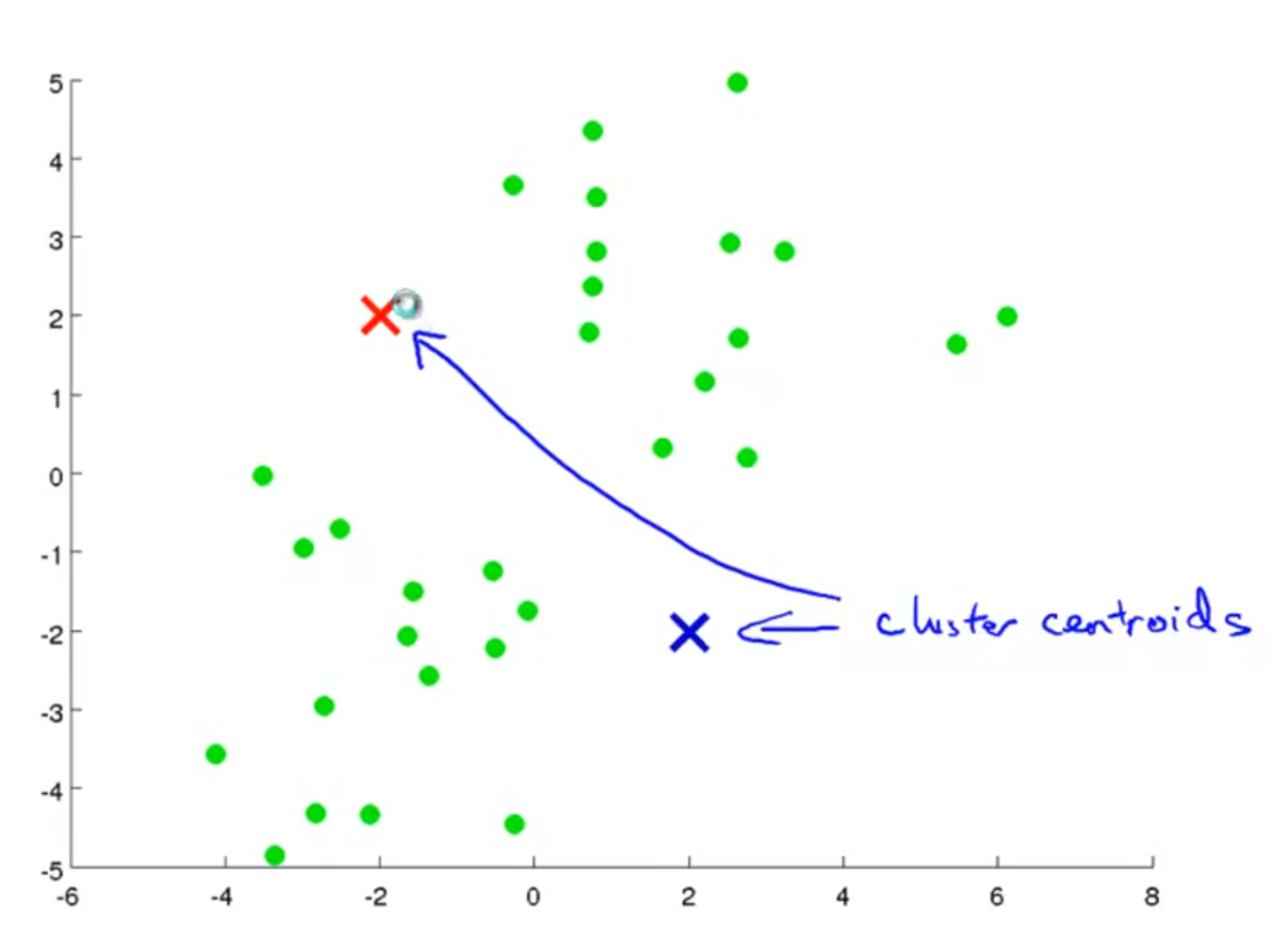
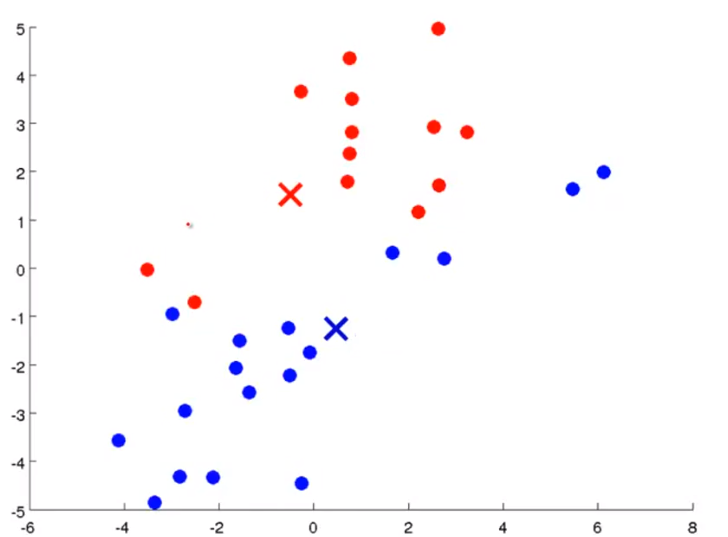
• 첫번째 작업으로는 K개의 클러스터 중심점을 할당해야 합니다. 위 슬라이드에서는 K=2라고 가정해 보겠습니다.
• 즉, cluster centroid는 2개가 되고 그 위치는 random으로 할당합니다.

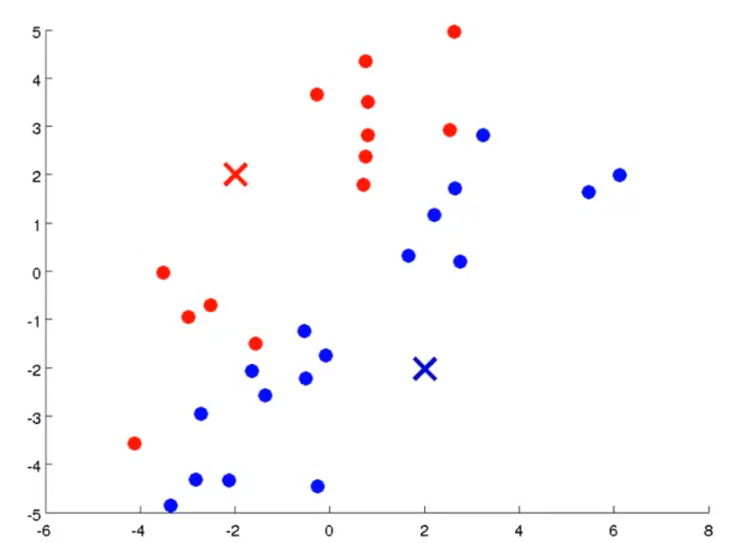
• centroid를 정하였다면 centroid와 가까운 점을 기준으로 clustering을 합니다.
• 위의 슬라이드를 보면 centroid와 가까운 점을 기준으로 빨간색 또는 파란색으로 clustering을 하였습니다.
  • 이 작업을 cluster assignment step 이라고 합니다.

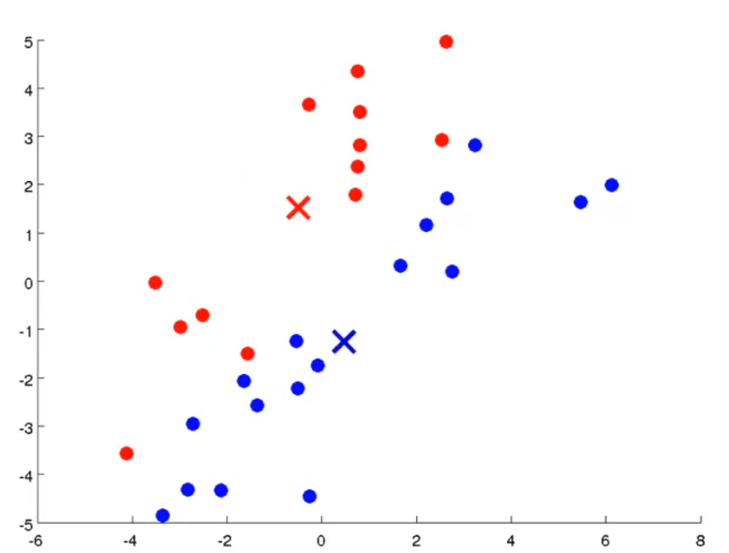
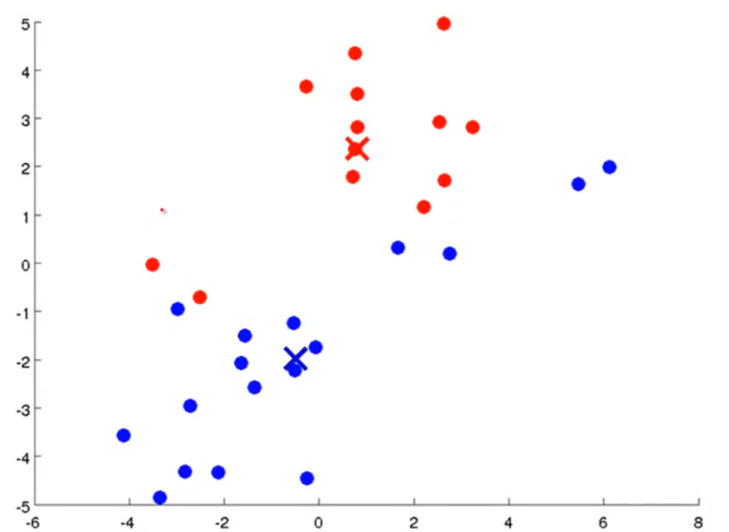
• 그 다음으로 같은 cluster 내의 데이터들의 평균 위치를 구합니다. 그리고 이 평균 위치 값을 새로운 centroid로 지정합니다.
• 그러면 위의 슬라이드와 같이 centroid가 움직이는 것을 알 수 있습니다.

• 이제는 앞에서 한 두 가지 스텝인 cluster assignment와 move centroid를 다시 반복해보겠습니다.
• 먼저 cluster assignment를 해보겠습니다.
• 위 슬라이드를 이전 슬라이드와 비교해 보면 데이터들이 재 배치되었습니다. 즉 centroid가 새로운 값으로 변경됨에 따라 데이터 중 일부가 cluster가 바뀌게 된 것입니다.

• 그 다음으로 move centroid를 해보면 centorid가 변경된 것을 볼 수 있습니다.

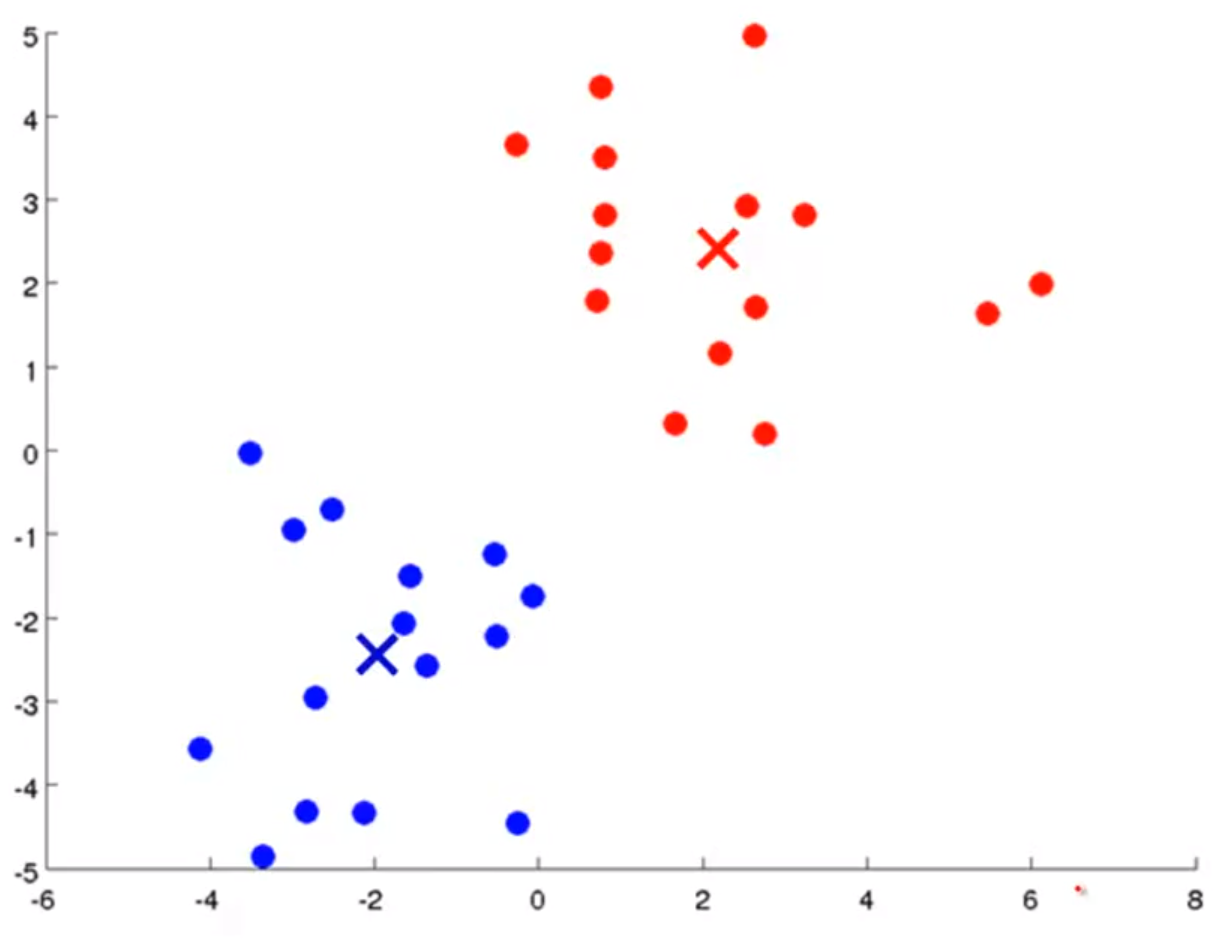
• 이 작업을 계속 반복해 보면, 위 슬라이드와 같은 clustering을 얻을 수 있습니다.
• 위와 같은 clustering을 얻기 위해서는 알고리즘 종료 조건이 필요합니다. 그 종료 조건은 클러스터를 구성하는 데이터가 더 이상 바뀌지 않고 수렴하게 되는 상태를 뜻합니다.
  • 위 알고리즘 전체를 보면 K-means 알고리즘은 iterative 알고리즘에 속하게 되고 알고리즘을 종료하기 위한 조건은 더 이상 상태 변화가 없을 때가 됩니다.

• K-means 알고리즘을 정리해 보도록 하겠습니다.

• 먼저 입력 값은 두 개 입니다.
  • 몇 개의 cluster로 나눌 지에 해당하는 K 입니다.
  • 그리고 Training data set이 필요합니다.
    • 이 때, 각각의 데이터는 n차원으로 표현할 수 있습니다.

• 위 슬라이드를 보면 k-means 알고리즘의 전체 프로세스를 간략하게 볼 수 있습니다.
• 첫번째로 할 일은 K개의 centroid를 랜덤하게 초기화를 해줍니다.
• 그 다음으로는 cluster assignment와 move centroid를 데이터의 수렴이 발생할 때 까지 계속 수행해 줍니다.
• 먼저, cluster assignment 과정을 보면 각각의 데이터 \(x^{(i)}\)는 \(c^{(i)} = min_{k} \Vert x^{(i)} - \mu_{k} \Vert^{2}\) 을 통해 어떤 클러스터에 속할 지 정해집니다.
• 클러스터가 정해지면 클러스터 \(c^{(i)}\) 에 속한 데이터들을 통하여 평균 값을 구할 수 있고 이 평균값이 세로운 centroid가 됩니다.

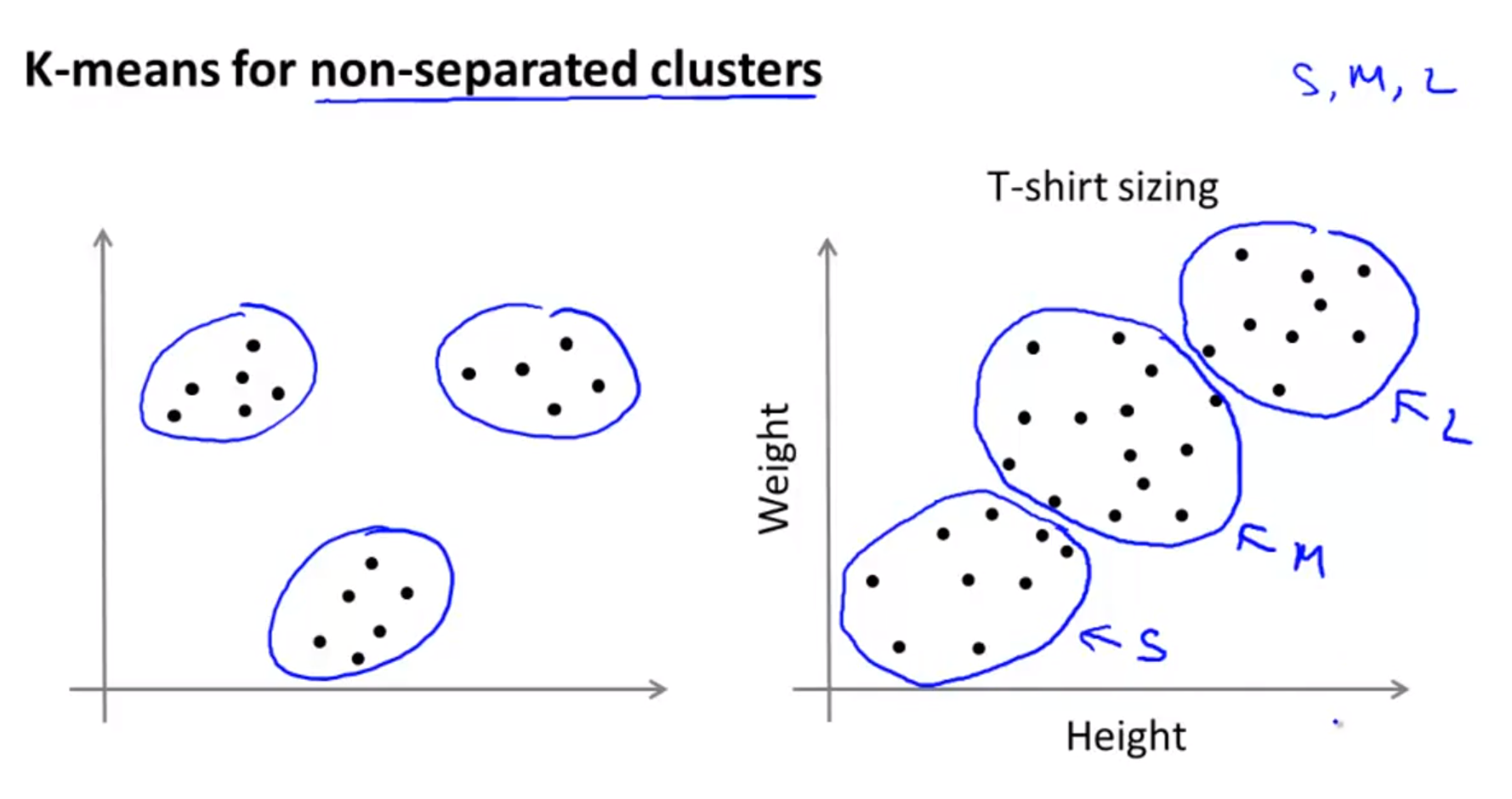
• K-means 알고리즘은 슬라이드 왼쪽 그림과 같이 명확히 데이터의 집합이 구분이 되어 있는 데이터셋을 구분할 수도 있지만
• 슬라이드 오른쪽 그림과 같이 클러스터가 분리되어 있지 않는 데이터 셋에서도 데이터를 분리할 수 있습니다.
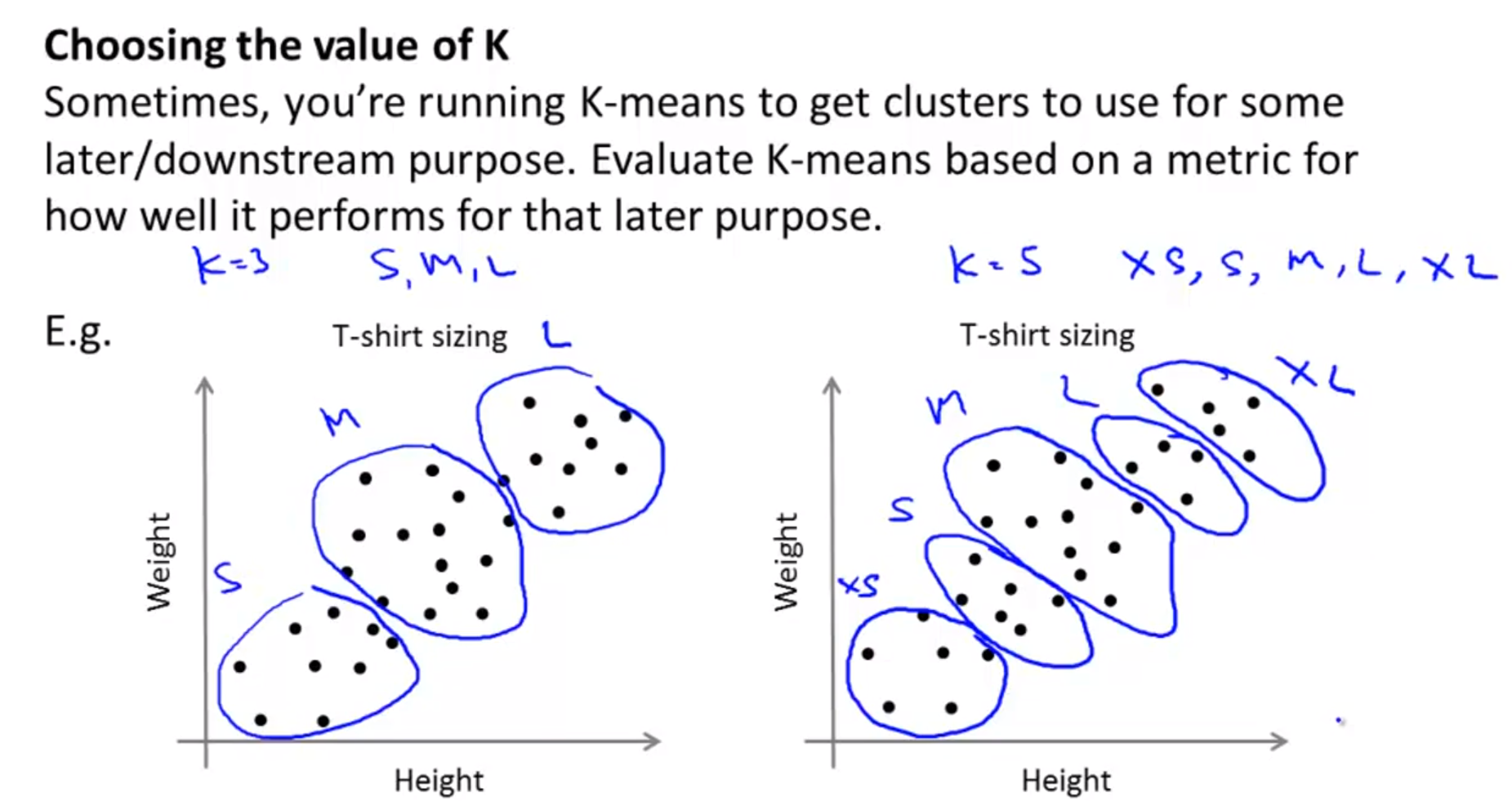
  • 오른쪽 그림의 예제를 market segmentation이라고 하고 예제에서는 몸무게와 키를 통하여 셔츠의 사이즈를 3부분으로 나눌 때 어떻게 나누어야 하는 지 기준을 제공해 줍니다.

Optimization objective

• 대부분의 supervised learning에서는 optimization을 하기 위한 방법들이 있었습니다.
  • 예를 들어 cost function을 최소화 하는것이 하나의 예가 됩니다.
• k-means 알고리즘에서도 optimize 해야하는 cost function이 존재합니다. 앞에서 살짝 언급하였기 때문에 눈치 채셨을 것입니다.
• k-means 알고리즘의 cost function에 대하여 알아보면 좋은 점이 있습니다.
  • 어떻게 디버깅 해야 하는 지 알 수 있고 학습이 잘 되고 있는지 또한 알 수 있습니다.
  • 더 좋은 cost와 로컬 미니마에 빠지는 것을 피할 수 있습니다.

• 먼저 \(c^{(i)}\) 는 데이터 \(x^{(i)}\) 가 어떤 클러스터에 속하였는 지 나타냅니다.
• 그리고 \(\mu_{k}\)는 \(k = \{1, 2, ..., k \}\) 에서 각 인덱스에 해당하는 클러스터의 중심인 centroid를 나타냅니다.
• 마지막으로 \(\mu_{c^{(i)}}\) 는 \(i\) 번째 데이터가 속한 클러스터의 centroid에 해당합니다.
  • 따라서 슬라이드의 예제와 같이 \(i\) 번째 데이터의 클러스터가 5이면 \(c^{(i)} = 5\)가 되고 \(\mu_{c^{(i)}} = \mu_{5}\) 가 됩니다.
• 위 세가지 정의를 기반으로 optimize 할 objective를 정의해 보면 위의 수식과 같습니다.
  • 제곱 형태의 계산을 보면 데이터와 클러스터의 중심 간의 거리 차이에 대한 평균을 구하고 있습니다.
  • 슬라이드의 오른쪽 하단을 보면 빨간색 선이 거리를 나타냅니다.
• 참고로 k-means 알고리즘의 cost function을 때때로 distortion 이라고 합니다.

• 다시 정리하면 앞에서 설명한 바와 같이 k-means 알고리즘은 cluster assignment와 move centroid 두 스텝을 통해서 구현됩니다.

Random Initialization

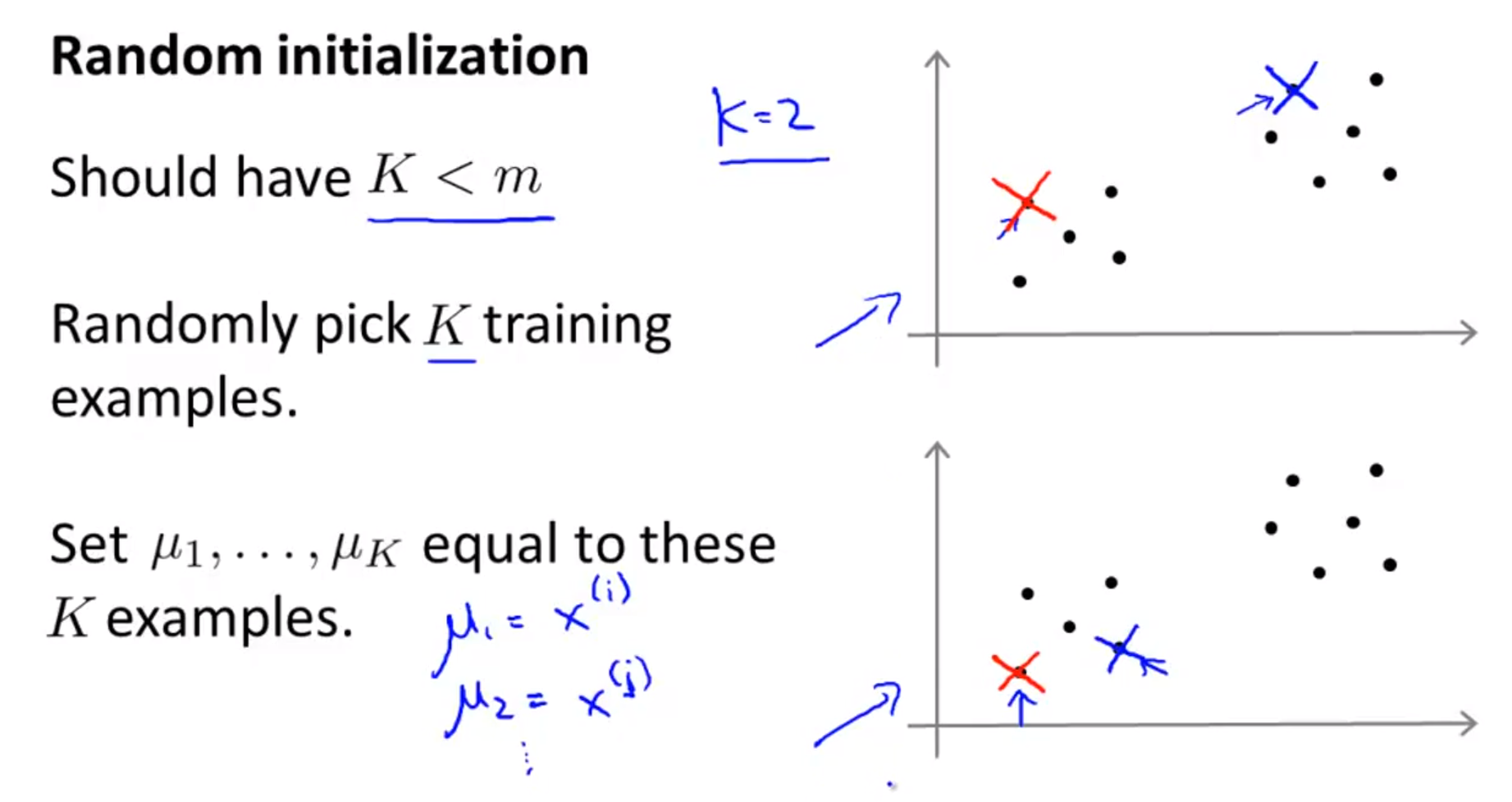
• 앞의 내용들을 숙지하였다면 한가지 궁금한 점이 있을 것입니다. 어떻게 centroid를 초기화 할 것인지에 대한 문제입니다.
• 먼저 초기화 할 centroid는 K개로 전체 데이터의 수 m개 보다 작아야 합니다.
• K개의 centroid는 데이터에서 뽑은 K개의 샘플을 이용하여 초기화 합니다.
  • 즉, K개의 샘플을 centroid로 잡습니다.
• 정리하면, \(K\) 개의 서로 다른 숫자 \(i_{1}, i_{2}, ..., i_{k}\) 를 \(\{1, 2, ..., m \}\) 에서 고른 뒤 \(\mu_{1} = x^{(i_{1})}, \mu_{2} = x^{(i_{2})}, ..., \mu_{k} = x^{(i_{k})}\) 로 세팅합니다.

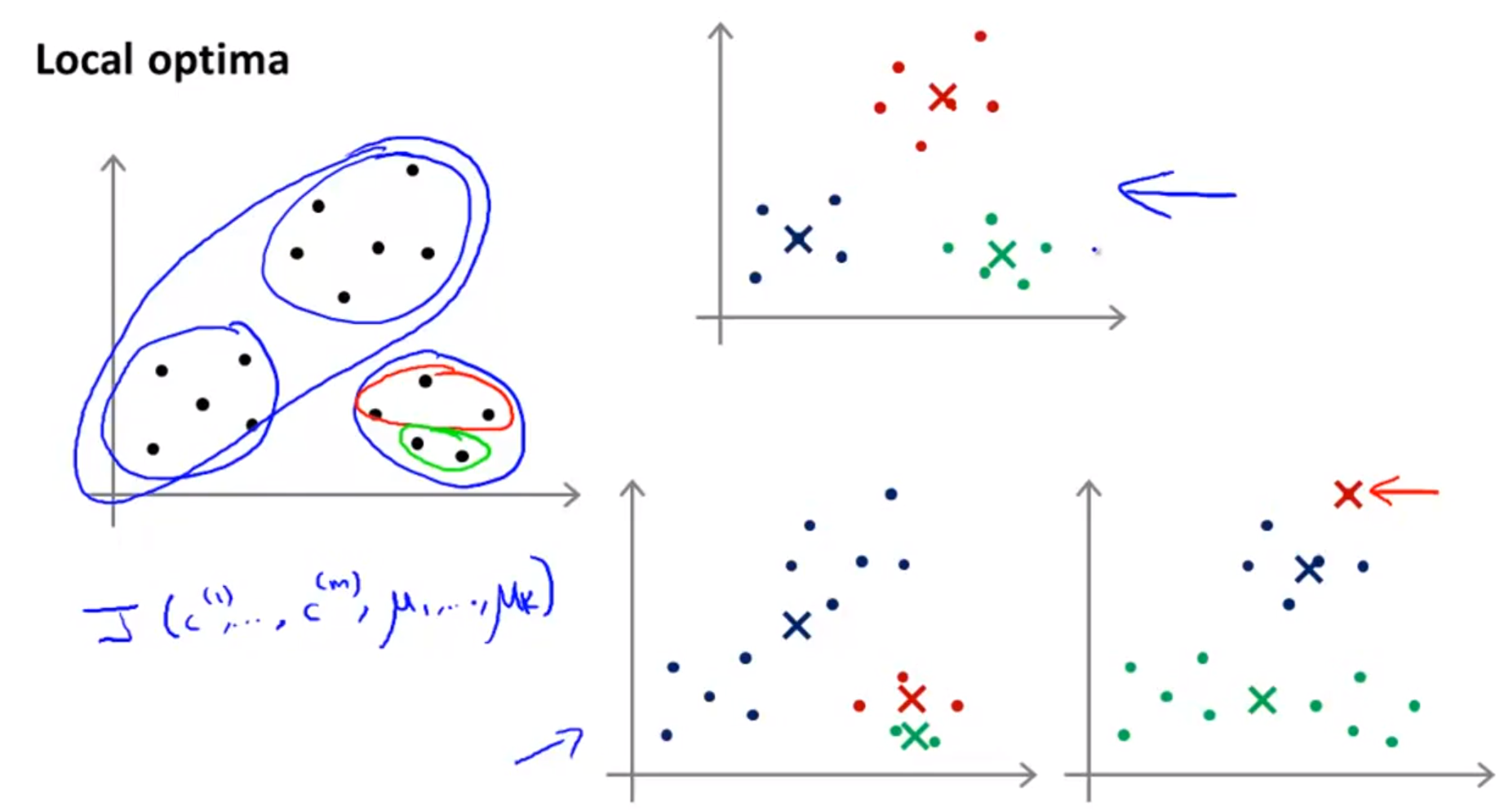
• 반면, Random Initialization을 하게 되었을 때 발생되는 문제는, local optima 입니다.
• local optima 문제는 최적화 문제에서 종종 나타나게 되는 문제 입니다.
• 슬라이드의 오른쪽 아래 2개의 그래프를 보면 처음 초기화를 잘못하게 되면 더 이상 개선되기 어려운 상태에 빠지게 되는 데 이러한 문제를 말합니다.
  • 즉, cost function을 더 이상 최소화 할 수 없는 상태입니다.

Choosing the Number of Clusters

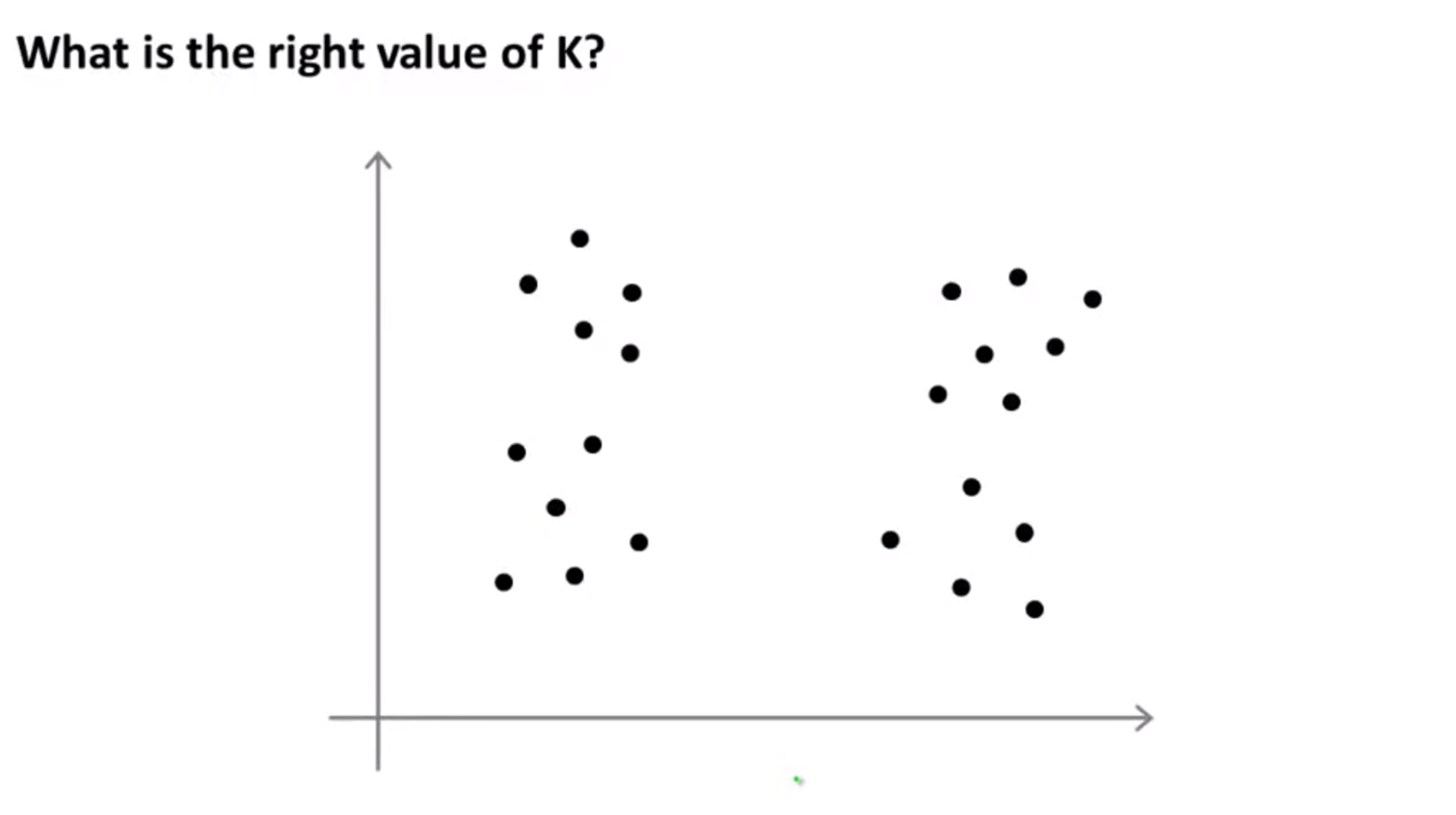
• 클러스터의 갯수 K는 어떻게 정하는 것이 좋을까요?

• 위와 같이 데이터의 분포가 있을 때, 사람이 수동으로 정하게 된다면 데이터의 분포를 보고 직관적으로 파악할 수 밖에 없습니다.

• 반면에, 앞에서 사용한 cost function을 이용하면 좀 더 수치적으로 접근할 수 있습니다.
• K-means 알고리즘에서는 K의 갯수가 너무 많다 보면 clustering이 너무 세분화 되어서 의미 있는 clustering을 구하기 어려울 수도 있습니다.
• 그러면 의미있는 clustering을 만들려면 적당한 갯수의 cluster(2 ~ 5개)가 있고 각 cluster가 적절한 의미를 가지고 있어야 합니다.
  • cluster가 의미가 있으려면 centroid가 각 클러스터를 잘 대표할 수 있도록 배치되어 있어서 clustering이 잘 되어 있다는 의미 입니다.
  • 즉, 각 cluster의 데이터 들과 centroid간의 차이가 최소화 되어 있어야 적절한 갯수의 클러스터로 적절하게 클러스터링 되어있다 라고 볼 수 있습니다.
• 앞에서 사용한 수치를 인용한다면, cost function이 작은 경우가 클러스터가 잘 된 경우라고 볼 수 있습니다.
• 하지만, 일반적으로 k가 늘어날수록 cost function이 작아지기 때문에 무작정 cost function이 작다고 좋은 클러스터링이라고 볼 수는 없습니다.
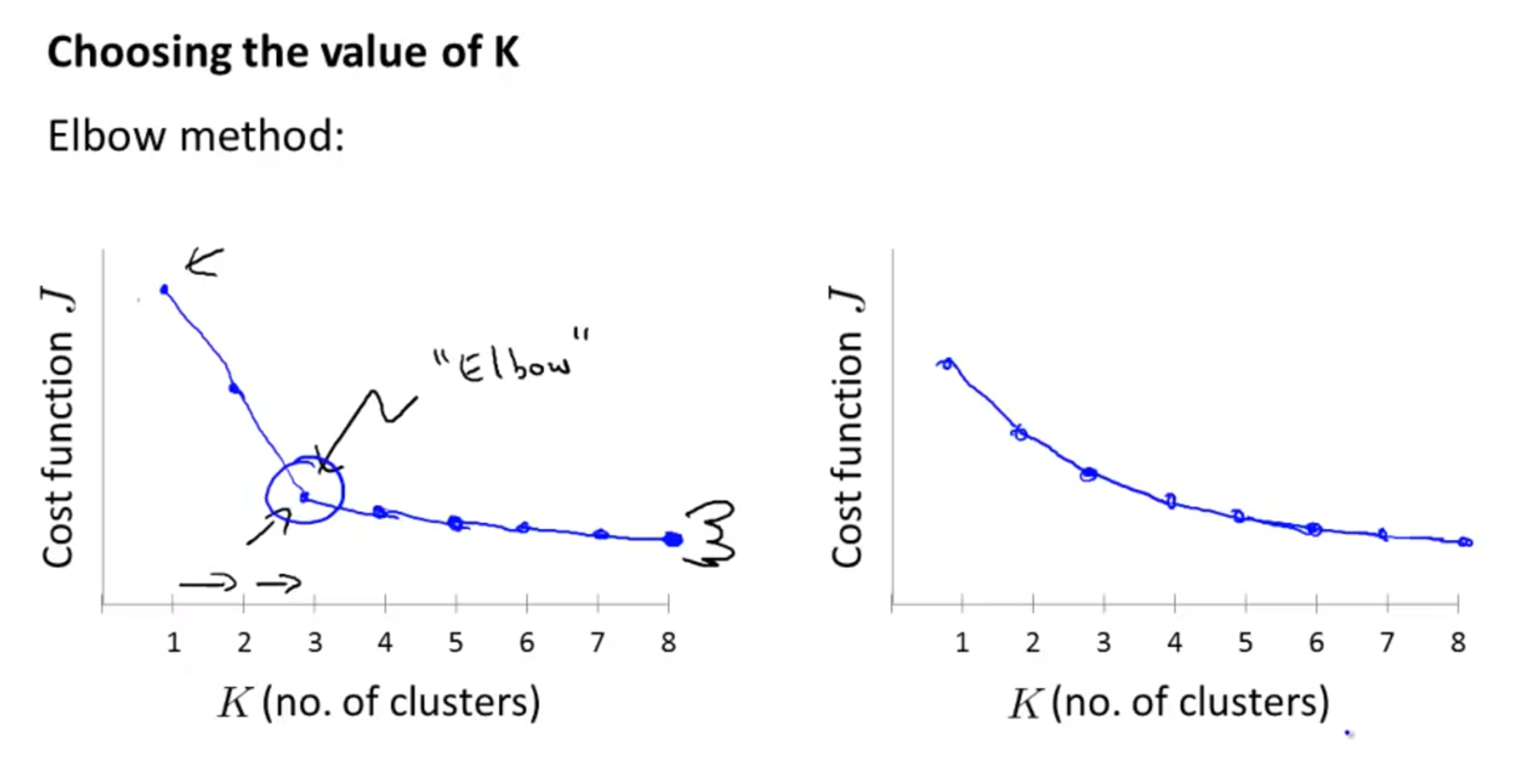
• 따라서 위 슬라이드와 같이 Elbow method를 사용하면 좋습니다.
  • 즉, Cost function이 급격하게 낮아지는 변곡점이 clustering이 의미가 있어지는 점의 K라고 볼 수 있습니다.

• 때로는 목적에 따라서, 클러스터링의 갯수를 정할 수도 있습니다.
• 위 슬라이드 왼쪽과 같이 클러스터링의 갯수가 3개가 필요하다는 것을 알고 있다면 3개만 적용할 수도 있고 오른쪽 처럼 5개가 필요하다면 5개를 직접 적용할 수도 있습니다.

K-means with scikit-learn

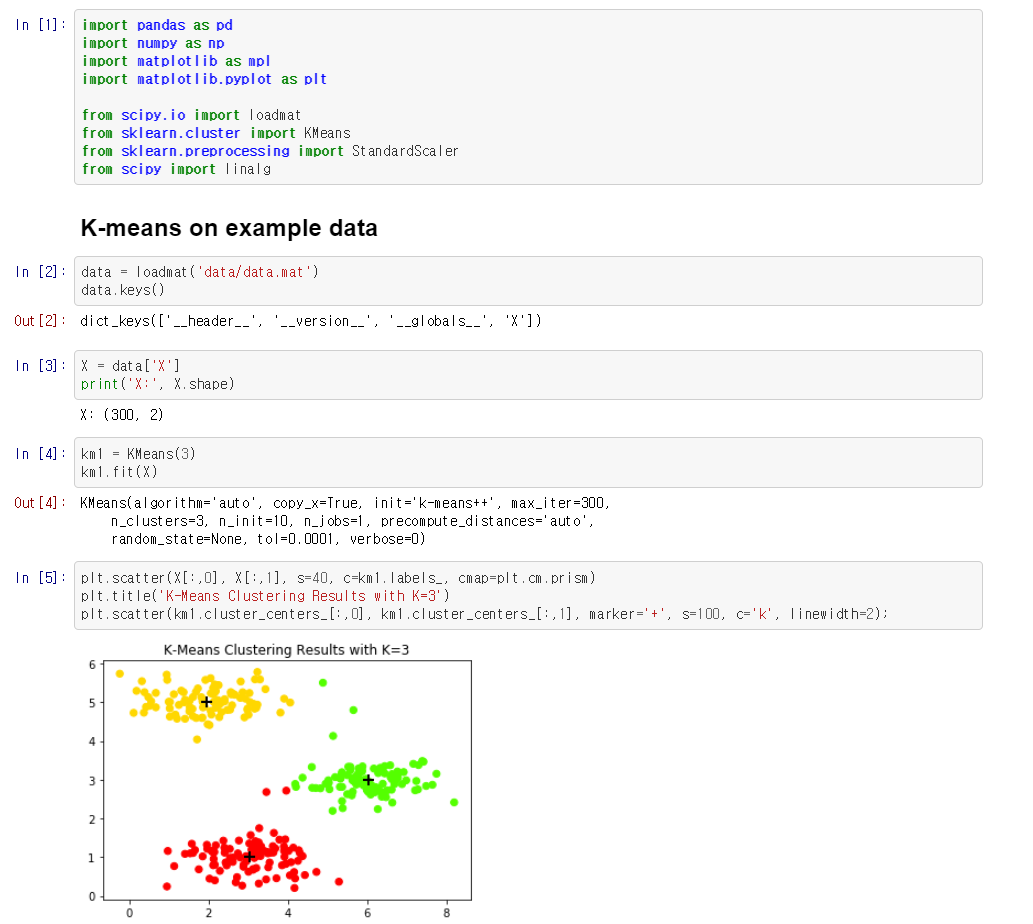
• 아래 코드 링크를 참조하면 scikit-learn을 이용하여 K-means 알고리즘을 사용하는 방법에 대하여 확인할 수 있습니다.
• 코드 링크