PCA(Principal Component Analysis) (Andrew Ng)

2019, Apr 02    

출처 : Andrew Ng 강의

Dimensionality Reduction

• 이번 글에서는 PCA(Principal Component Analysis)에 대하여 알아보도록 하겠습니다.
• PCA에 대하여 자세히 알아보기 전에 unsupervised learning의 한 종류에 해당하는 dimensionality reduction에 대하여 먼저 살펴보도록 하겠습니다.
• 그 중 첫번째로 살펴볼 dimensionality reduction의 역할은 compressing the data 입니다.

• 만약 데이터를 표현하는 feature가 여러개가 있다고 가정해 보겠습니다. 위 슬라이드에서는 간단하게 표현하기 위해서 feature가 2개 있다고 가정하겠습니다.
• 위 슬라이드의 2개의 feature는 사실 중복된 feature라고 볼 수 있습니다. 둘 다 길이를 나타내기 때문입니다.
  • 만약 수십, 수백개의 feature가 있다고 하더라도 그 중에서는 여러개의 중복된 feature가 분명히 있을 수 있습니다.
• 따라서 중복된 feature를 하나로 줄이기 위하여 현재 분포된 데이터 상에서 데이터를 표현하는 파란색선을 그려보면 위와 같습니다.

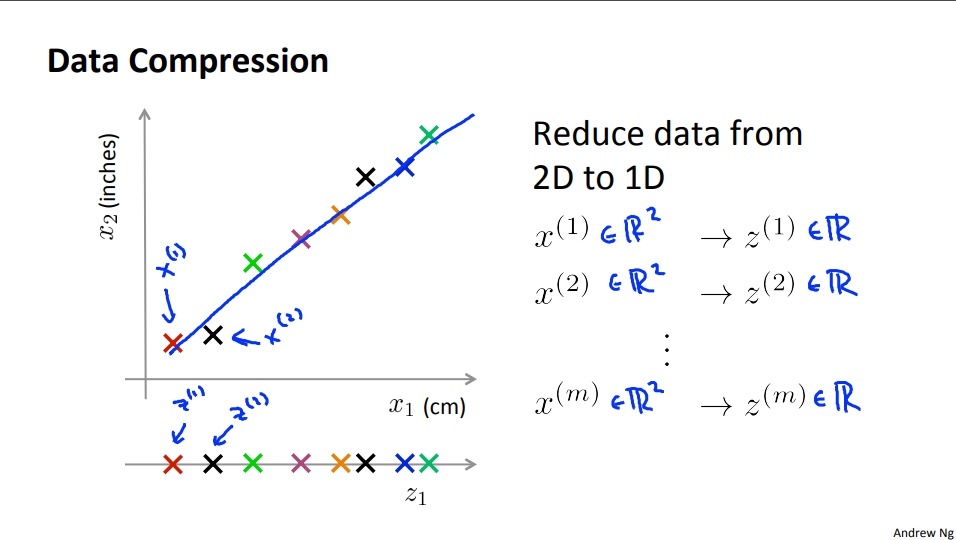
• 이 새로운 선은 새로운 feature라고 생각할 수 있습니다. 이 새로운 선으로 데이터를 표현하면 2개의 feature인 \(x^{(1)}, x^{(2)}\) 대신에 새로운 feature인 \(z^{(1)}\)으로 대신 표현할 수 있습니다.

• 그러면 원래 데이터에 해당하는 \(x^{(i)} \in \mathbb R^{2}\)는 \(z^{(i)} \in \mathbb R^{(1)}\)로 대응되게 됩니다.

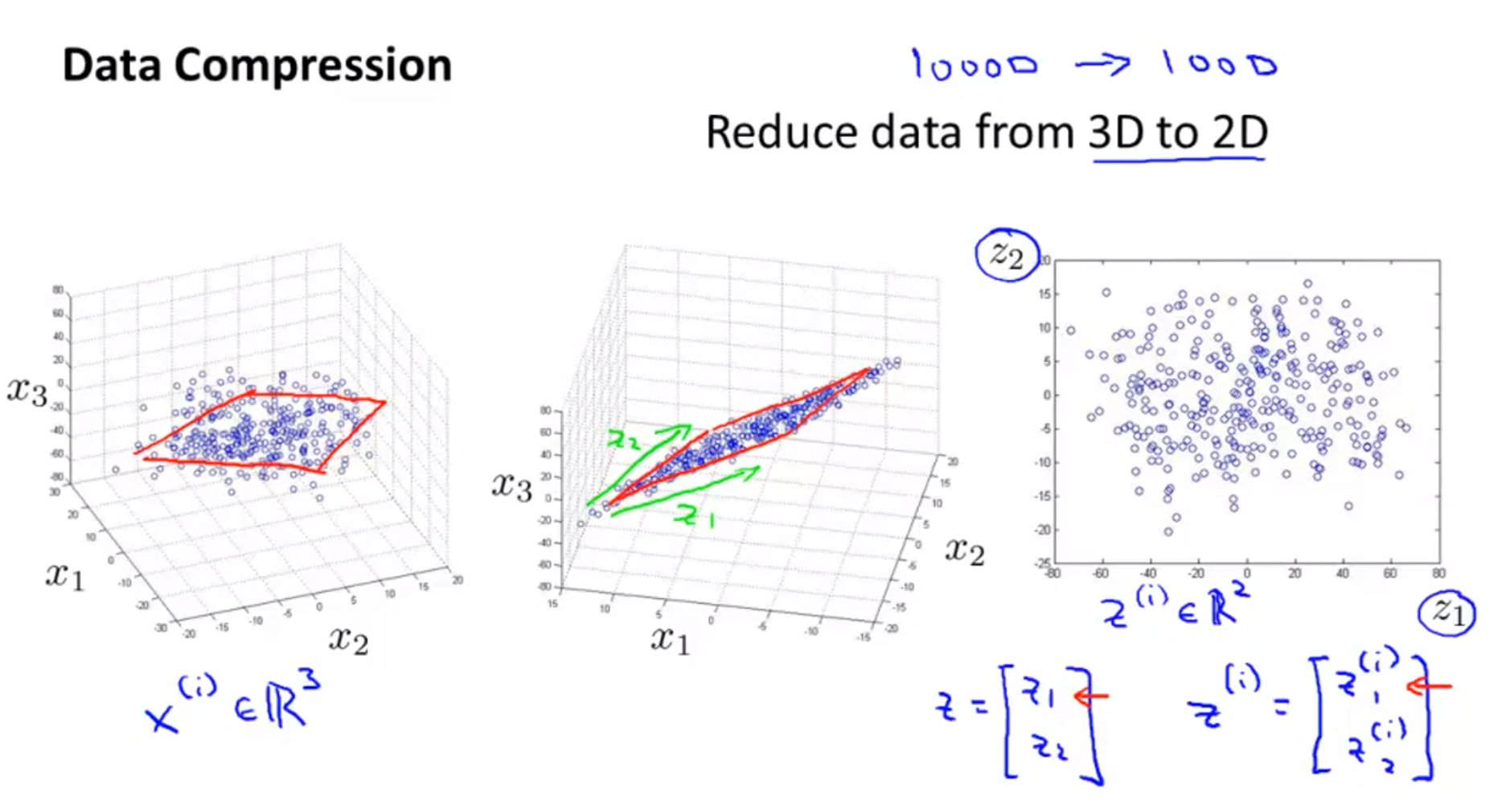
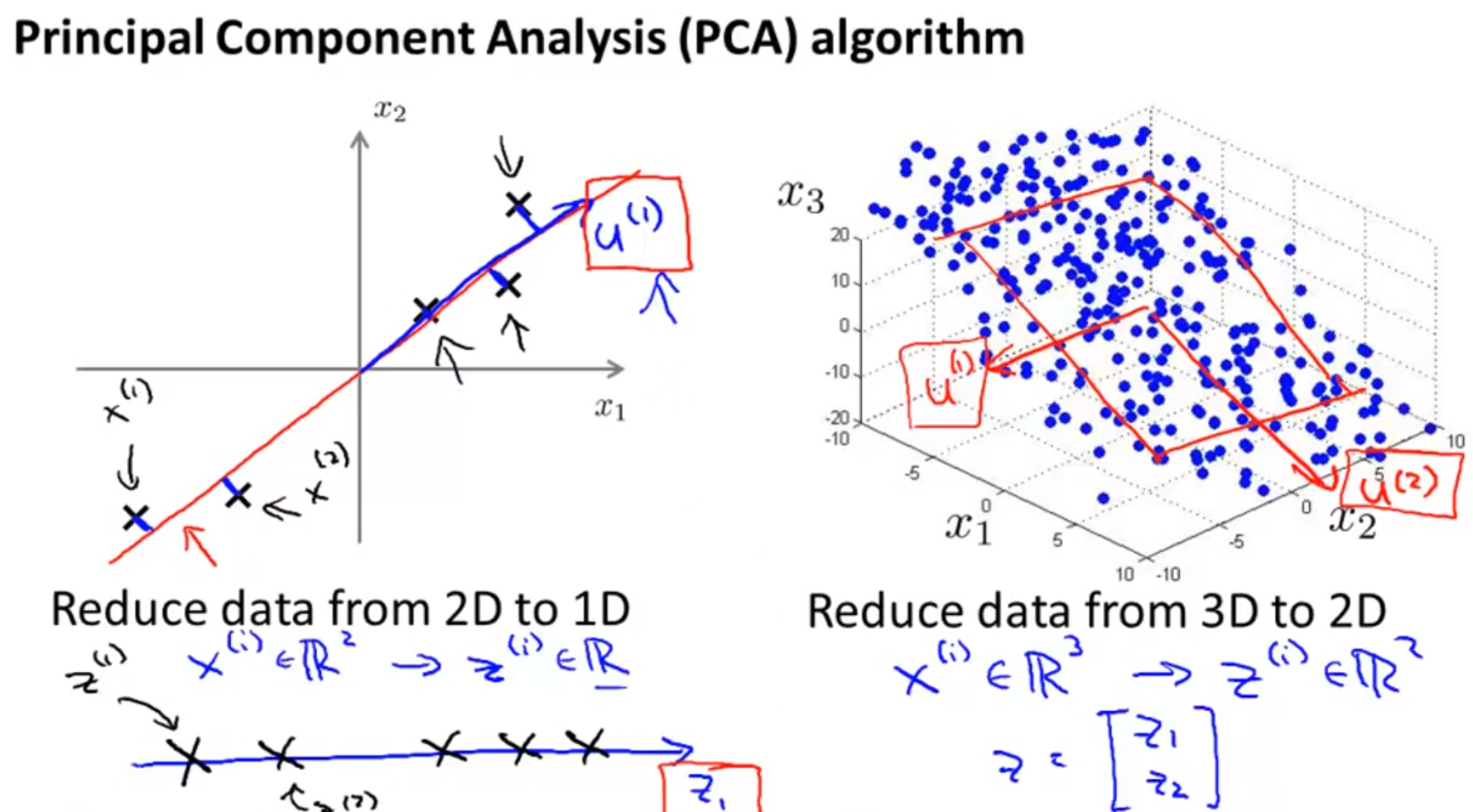
• 위 슬라이드에서는 조금 더 차원을 확장해서 3차원을 2차원으로 축소해 보도록 하겠습니다. 즉, feature의 갯수가 3개에서 2개로 축소하는 것입니다.
• 방법은 앞에 방법과 동일합니다. 기존의 feature인 \(x^{(1)}, x^{(2)}, x^{(3)}\)을 이용하여 표현한 공간에 새로운 feature인 \(z^{(1)}, z^{(2)}\) 만을 이용하여 데이터를 표현합니다.
• 즉, 공간에서 그려졌던 데이터가 평면에 표현된 것을 볼 수 있습니다.

• 지금까지 살펴본 것을 이용하여 dimensionality reduction에 대하여 정의해 보면
• 만약 데이터가 \(\{x^{(1)}, x^{(2)}, ... , x^{(m)} \}, x^{(i)} \in \mathbb R^{n}\)이 있을 때,
• lower dimensional dataset은 \(\{z^{(1)}, z^{(2)}, ... , z^{(m)} \}, z^{(i)} \in \mathbb R^{k}, k \le n\) 입니다.

• 추가적으로 dimensionality reduction의 또 다른 역할 중 하나인 data visualization에 대하여 알아보도록 하겠습니다.
• 먼저 데이터를 시각화하면 어떤 장점이 있을까요? 간단하게 말하면 데이터에 대한 분포를 눈으로 쉽게 확인 할 수 있고 데이터에 대한 이해도 증가하게 됩니다.

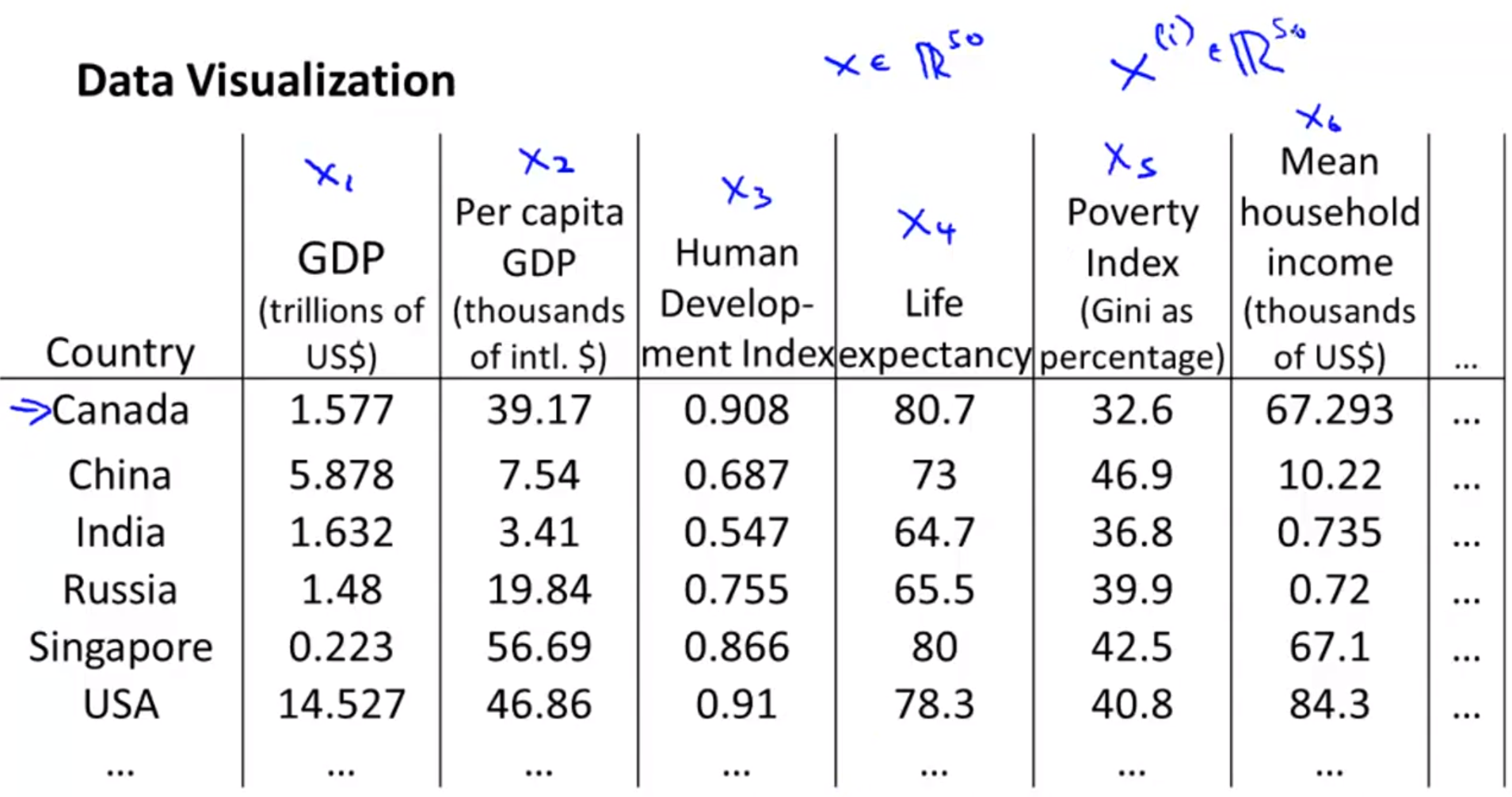
• 만약 위 슬라이드 처럼 여러개의 feature들이 있다면(GDP, Life, Poverty, …) 각 나라의 특성을 한눈에 확인하기가 어렵습니다.
  • 즉, 데이터의 특성에 대한 이해도가 떨어질 수 있습니다.

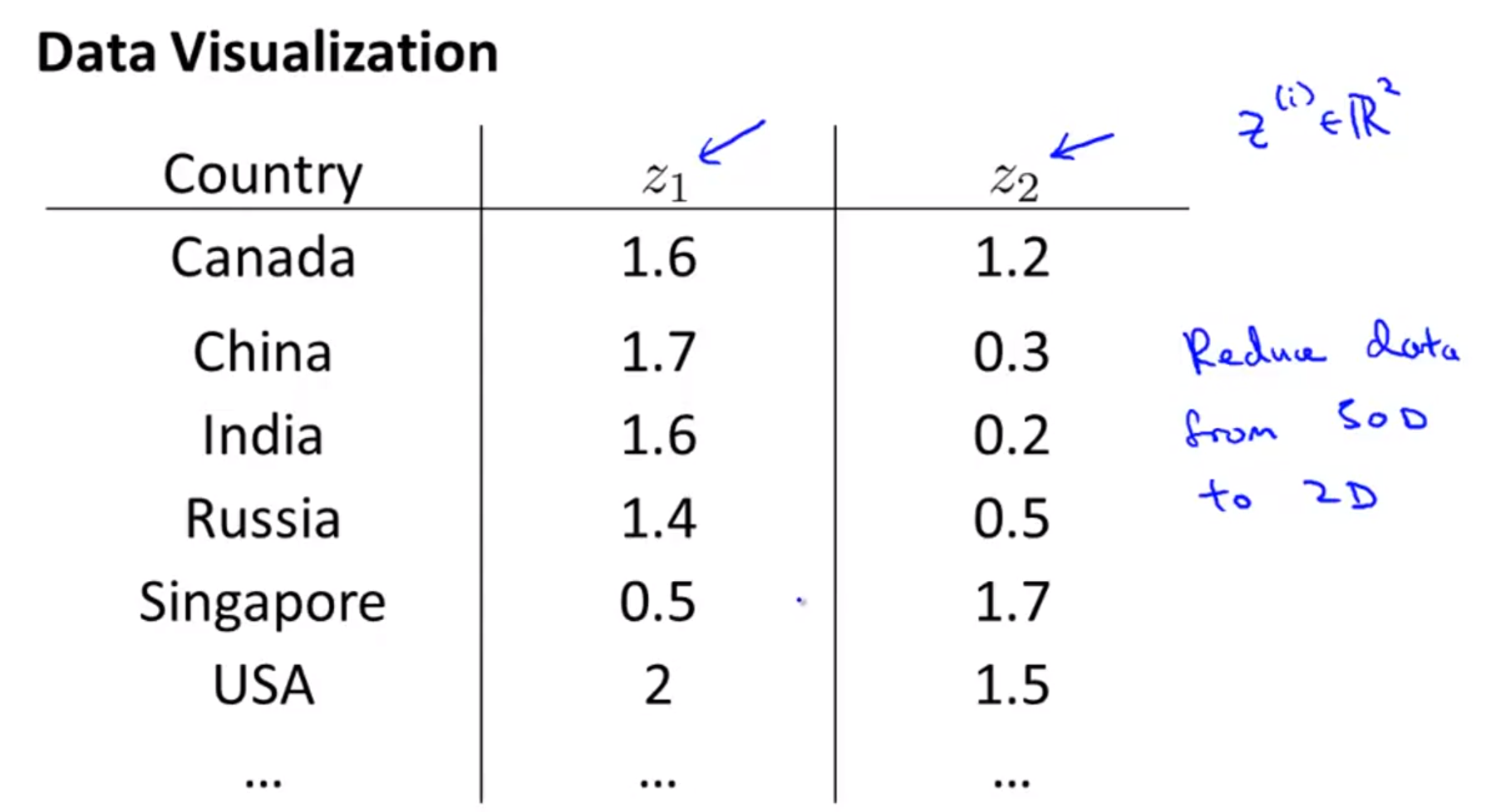
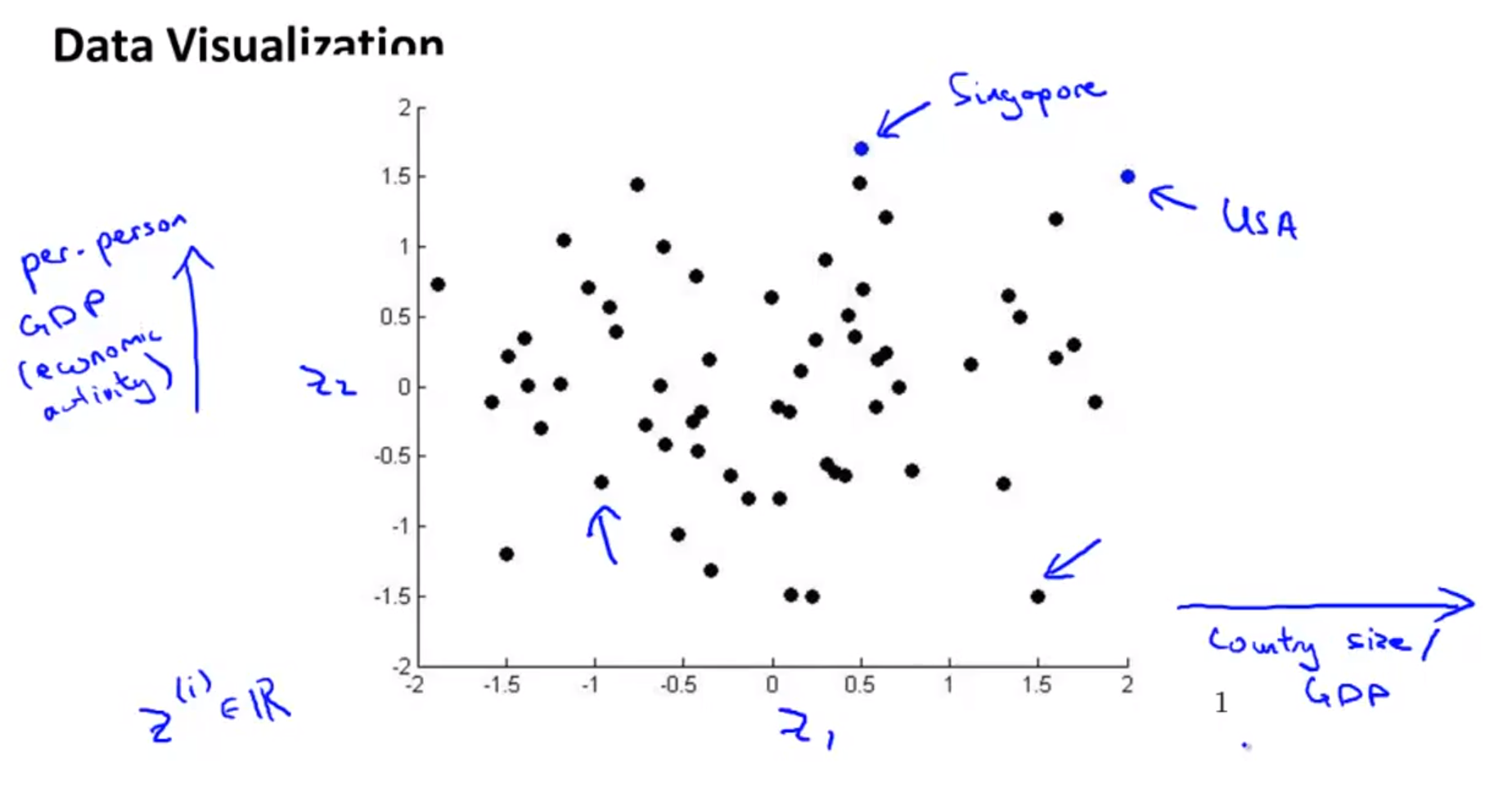
• 반면 위 슬라이드 처럼 단 2개의 새로운 feature로 데이터를 표현한다면 새로운 공간에 데이터들을 projection할 수 있고, 클래스들 간의 분포등을 쉽게 볼 수 있습니다.

• 예를 들어 새로운 feature가 뜻하는 것이 위 처럼 country size/GDP 처럼 특정 의미를 지니게도 만들 수 있습니다.
• 하지만 위 처럼 인위적으로 feature를 새로 만들어서 feature의 갯수를 줄인다기 보다는 좀 더 수학적으로 데이터들을 잘 표현할 수 있도록 대표하는 feature를 만드는 방법을 사용할 예정입니다.

PCA(Principal Component Analysis)

• 대표적인 dimensionality reduction 방법중의 하나인 PCA(Principal Component Analysis)에 대하여 알아보도록 하겠습니다.

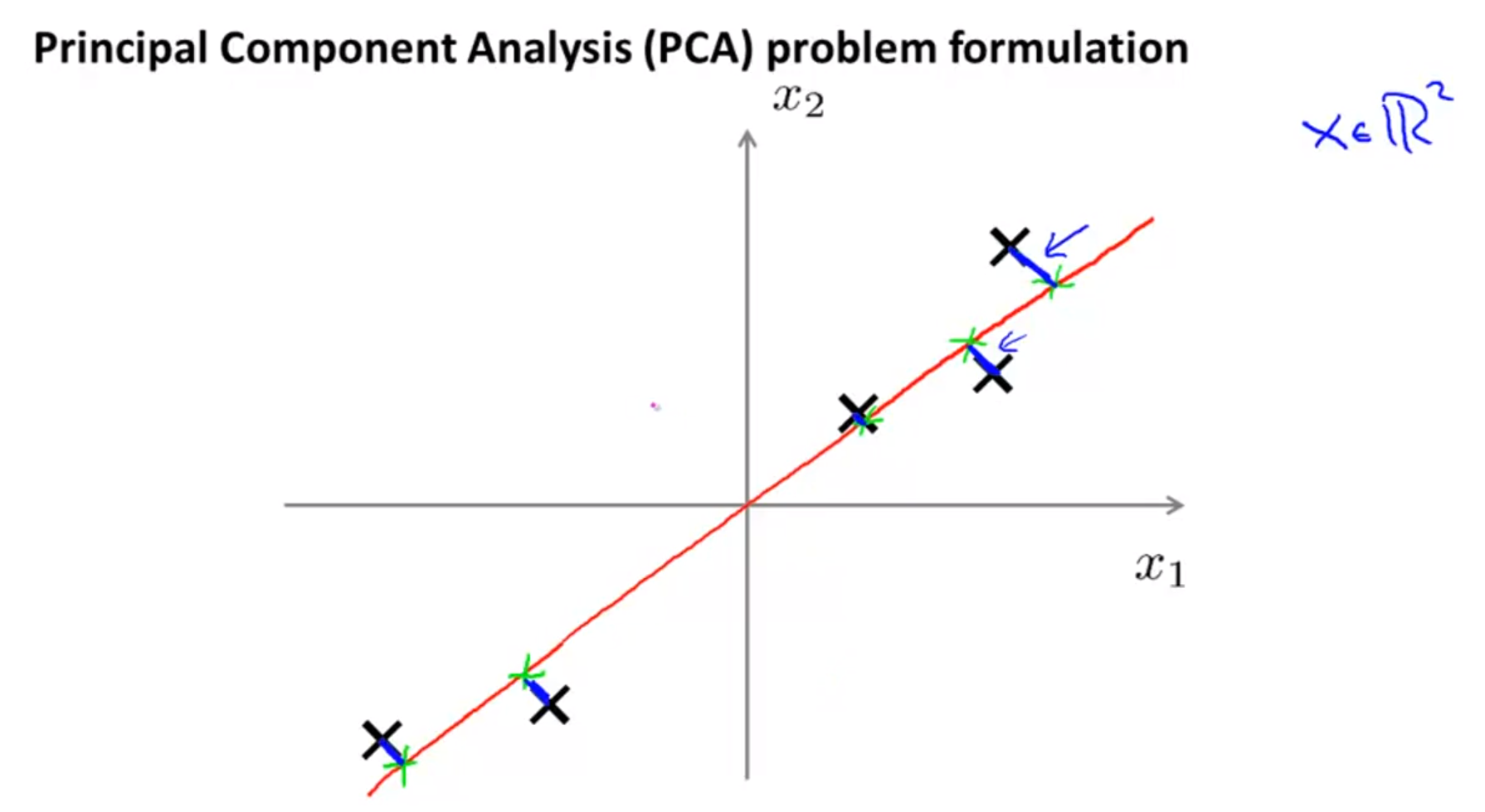
• 위의 슬라이드와 같이 검은색 좌표들 처럼 데이터가 분포가 되어 있다고 가정해 봅시다.
• 위 슬라이드의 데이터는 2차원 좌표에 분포해 있으므로 차원을 줄이려면 1차원 즉, 선 하나에 데이터를 위치시켜야 합니다.
• 따라서 데이터들을 빨간색 선에 위치 시키도록 해보겠습니다.
• 그러면 여기서 빨간색 선을 어떻게 구할 수 있을까요? 방법중의 하나는 검은색 점들을 정사영시켰을 때의 좌표들을 선으로 잇는 방법이 있습니다.
• 이 방법으로 저차원의 공간(여기서는 1차원이므로 선)을 구하면 여러가지가 나올 수 있습니다.
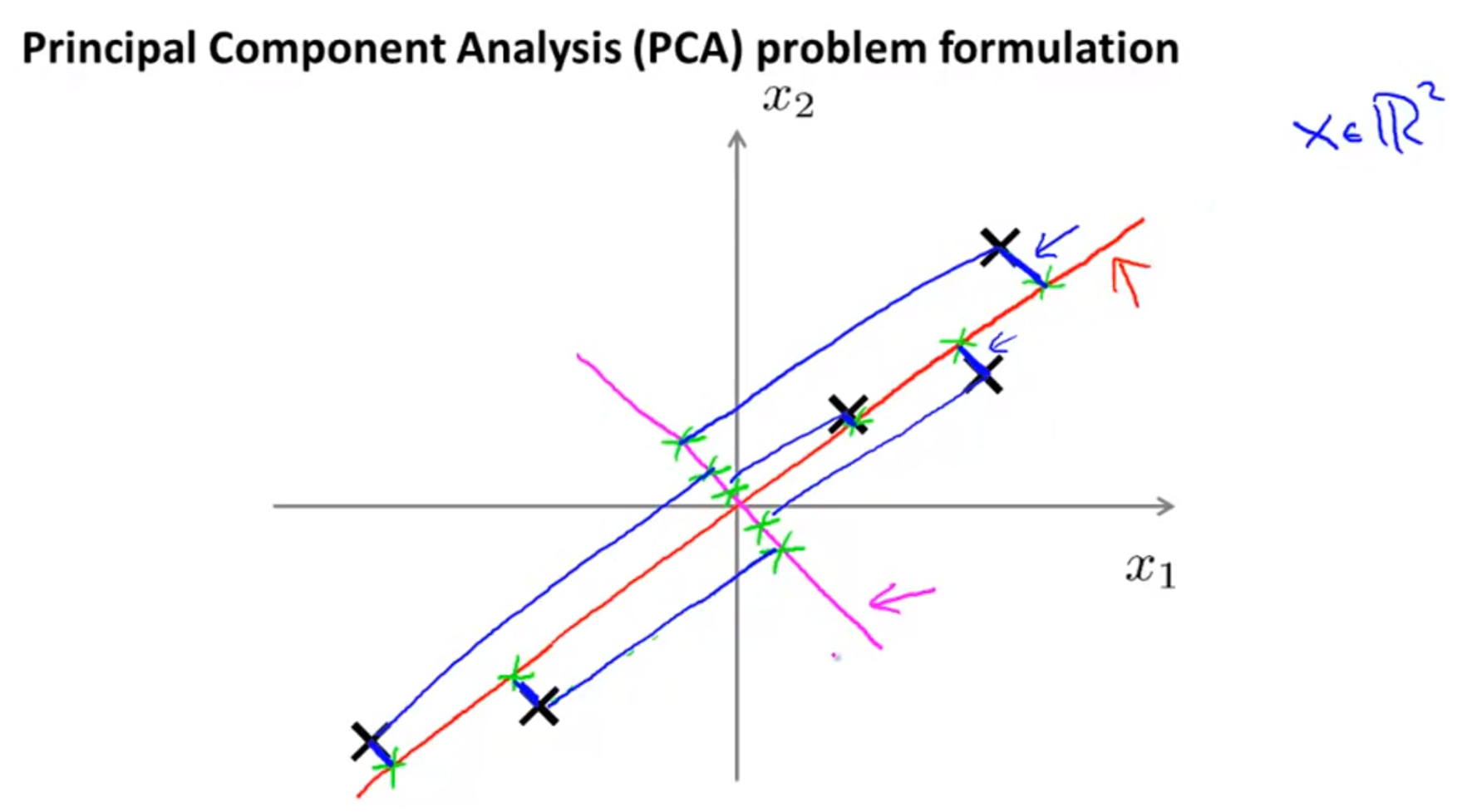
• 이 때 정사영시킨 거리(파란색선)의 합이 최소가 되도록 하는 선을 구하면 모든 데이터들을 가장 잘 표현할 수 있는 새로운 차원의 축을 만들 수 있습니다.
  • 참고로 파란색선을 projection error 라고 합니다.

• 예를 들어 위의 자주색 선의 projection error를 보면 빨간색 선에 비해서 상당히 큰 것을 볼 수 있습니다.
  • 이런 이유로 자주색 선 같은 정사영의 집합으로 이루어진 새로운 축 보다는 빨간색 선 같은 축이 선택됨을 알 수 있습니다.

• 위 방법을 이용하여 데이터를 정사영시킬 새로운 공간(선, 면등)을 찾는 방법을 PCA 라고 합니다.

• PCA에 대한 내용을 정리하면 앞에서 살펴본 바와 같이 2차원 데이터를 1차원으로 차원 축소 시킬 때, 데이터들을 1차원으로 정사영시킬 벡터를 찾았습니다.
  • 이 때, 벡터는 projection error를 최소로 만들 수 있는 벡터라는 점을 이용하여 찾았습니다.
• 이것을 일반화 시켜서 n차원 데이터를 k차원 데이터로 차원 축소를 시킨다면 어떻게 할 수 있을까요?
• 이 때에는 k개의 벡터를 찾아야 합니다. 이 때 벡터를 \(u^{(1)}, u^{(2)}, ..., u^{(k)}\) 라고 할 수 있습니다.
• 이 때 찾은 k개의 벡터를 이용하여 공간을 만들고 데이터들을 k개의 벡터들로 만든 공간안에 정사영 시킬 수 있습니다.
  • 같은 원리로 k개의 벡터들은 데이터들을 정사영시켰을 때 projection error가 최소가 되는 벡터들 입니다.
  • 그리고 선형대수학의 이론을 빌려서 표현하면 k개의 벡터로 표현한 공간은 \(span\{ u^{(1)}, u^{(2)}, ..., u^{(k)} \}\) 가 됩니다.

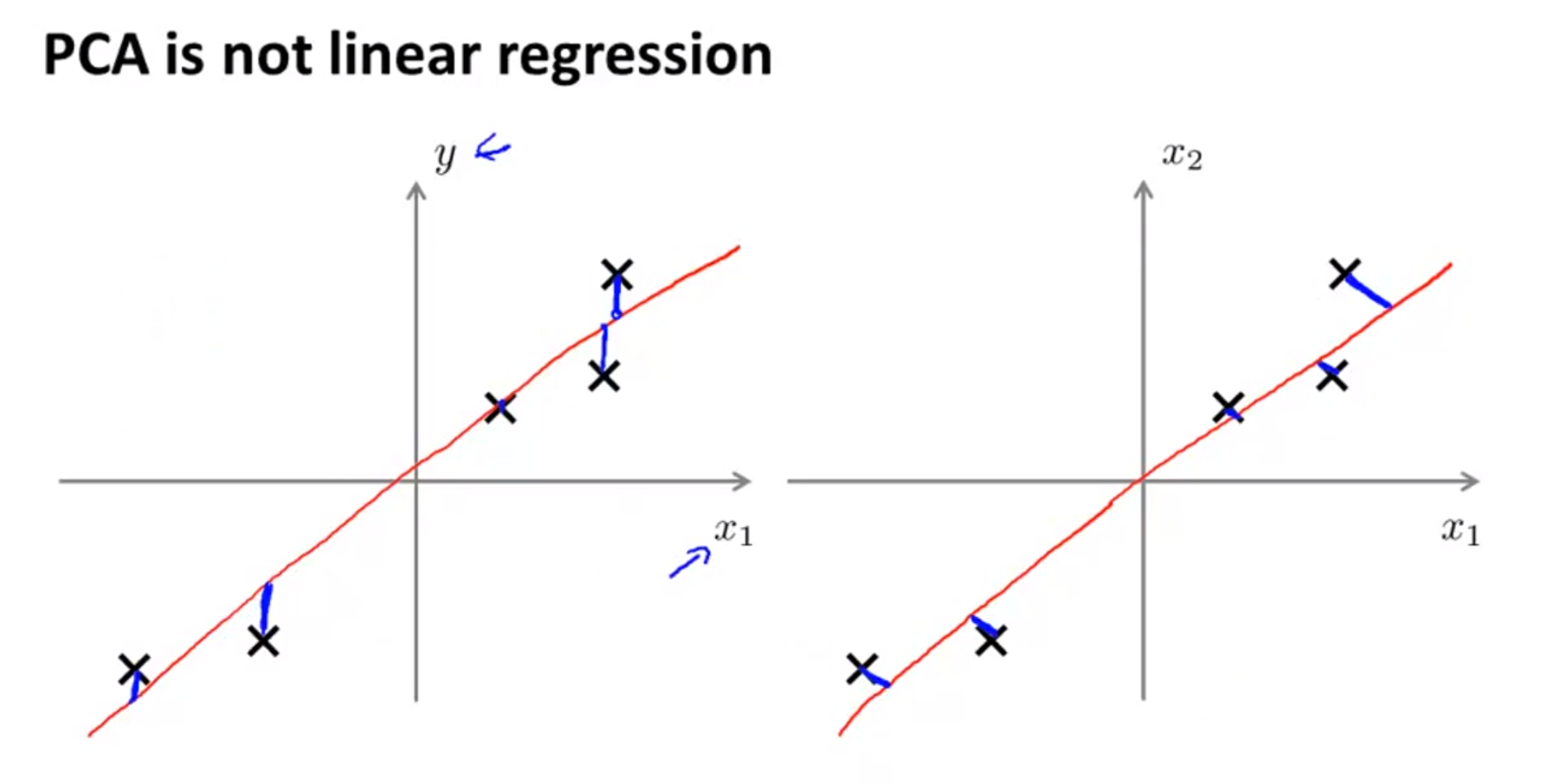
• 간혹 PCA를 이용하는 것과 linear regression하는 것을 헷갈릴 수도 있습니다. 하지만 큰 차이가 있습니다.

• 위 슬라이드를 보면 왼쪽은 linear regression이고 오른쪽은 PCA입니다.
  • 왼쪽을 보면 데이터와 선의 점간의 거리 차를 계산하는 것입니다.
  • 오른쪽을 보면 데이터들을 정사영 시킨 것입니다.
• 또한 왼쪽의 linear regression에서는 정답 데이터가 필요한 반면 오른쪽의 PCA에서는 정답 데이터가 필요없는 차이점도 있습니다.
  • 즉 linear regression은 supervised learning 방법으로 prediction을 하는 것인 반면
  • PCA는 projection을 할 새로운 차원을 만들어내는 unsupervised learning 방법입니다.

• 그러면 PCA를 구하려면 어떻게 구해야 하는지 좀 더 수식적으로 알아보도록 하겠습니다.
• 먼저 PCA를 하기 전에 데이터 전처리를 해주어야 합니다. 즉 데이터에 대하여 normalization을 합니다.

• normalization을 해주는 이유는 데이터들이 유사한 범위의 값을 가지도록 하기 위해서 입니다.

• PCA 연산을 하면 두가지 결과를 얻을 수 있습니다.
  • 위 슬라이드에서 표현되는 새로운 공간 축인 \(u^{(i)}\) 입니다.
  • 그리고 새로운 공간 축에 대응되는 새로운 데이터의 값인 \(z^{(i)}\) 입니다.

• 다음으로 PCA를 하려면 n차원의 데이터를 k차원으로 줄여야 하는데 이 때 사용할 방법이 공분산과 고유벡터입니다.
• 먼저 n차원 데이터 \(x^{(i)}\) 에 대한 공분산을 구해야 합니다.
  • 위 슬라이드에서 각 데이터 \(x^{(i)}\)는 n차원이므로 (n x 1) 벡터로 표현할 수 있고 데이터의 갯수가 m개 이므로 m으로 평균을 만들어서 공분산을 구해줍니다.
• 공분산을 이용해서 특이값 분해를 하면 고유벡터를 구할 수 있습니다.
  • 특이값 분해(SVD)는 다음 링크를 참조하시기 바랍니다
    • https://gaussian37.github.io/math-la-linear-algebra-basic/
• 이 때 행렬 \(U\)는 (n x n)의 크기를 가지게 되고 여기서 k개를 선택하면 차원의 수를 k개로 줄일 수 있습니다.
• 즉 정리하면,
  • 1 ) 공분산 행렬을 구합니다.
  • 2 ) 공분산 행렬의 고유벡터를 구합니다.
  • 3 ) 고유벡터에서 k개 만큼 선택하여 차원의 갯수를 k개로 줄입니다.
• 이 방법이 PCA의 핵심입니다.

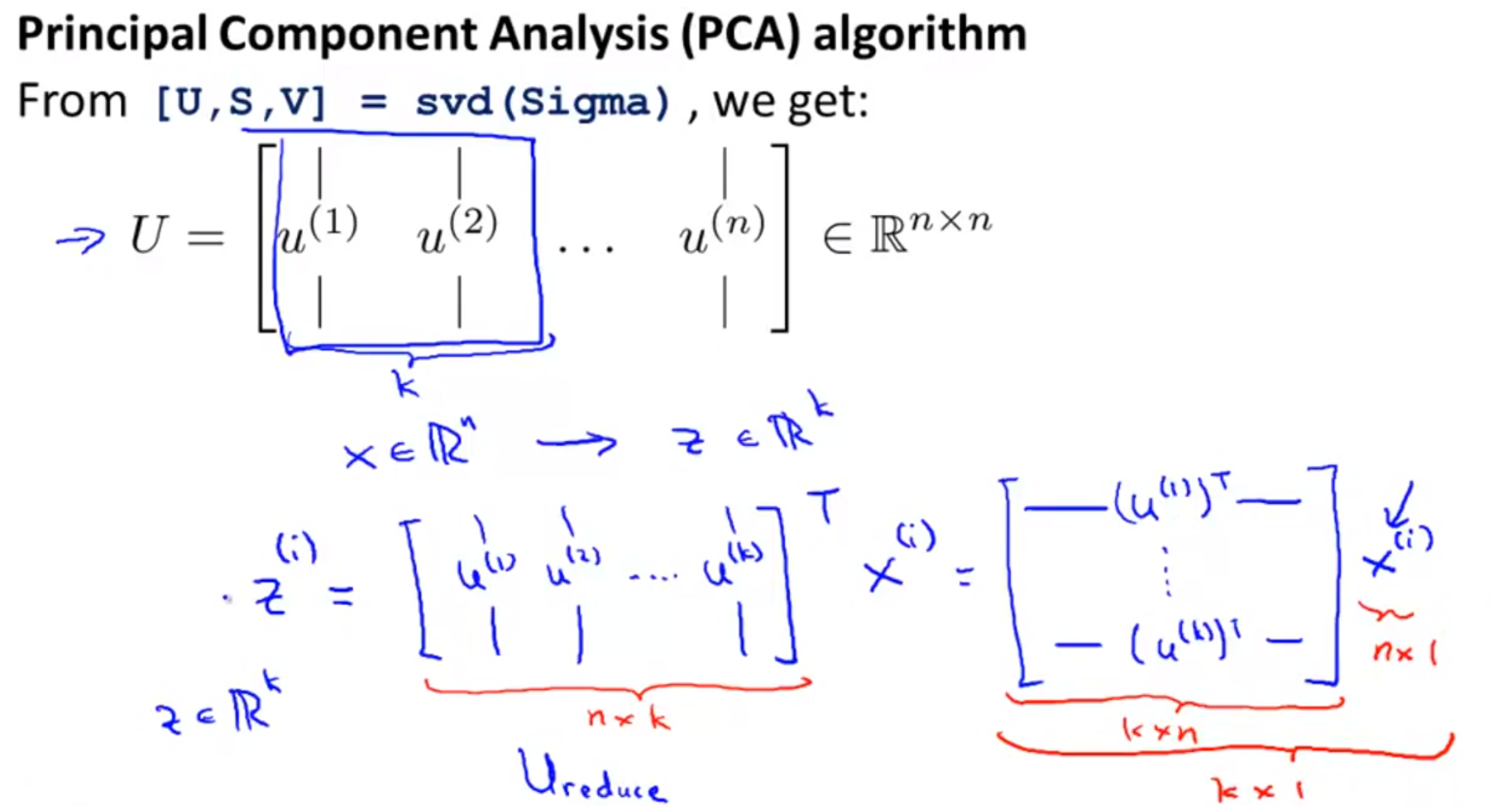
• 좀 더 풀어서 살펴보면 행렬 \(U\) 는 위와 같이 (n x k)의 크기를 가지게 됩니다.
• 새로운 공간에 값을 projection시킨 값 \(z^{(i)}\)를 구하려면 \(z^{(i)} = U^{T}x^{(i)}\)를 통하여 (k x 1) 크기의 벡터를 구할 수 있습니다.

• 따라서 코드로 PCA를 표현하면 위와 같이 쉽게 나타낼 수 있습니다.

Reconstruction from compressed representation

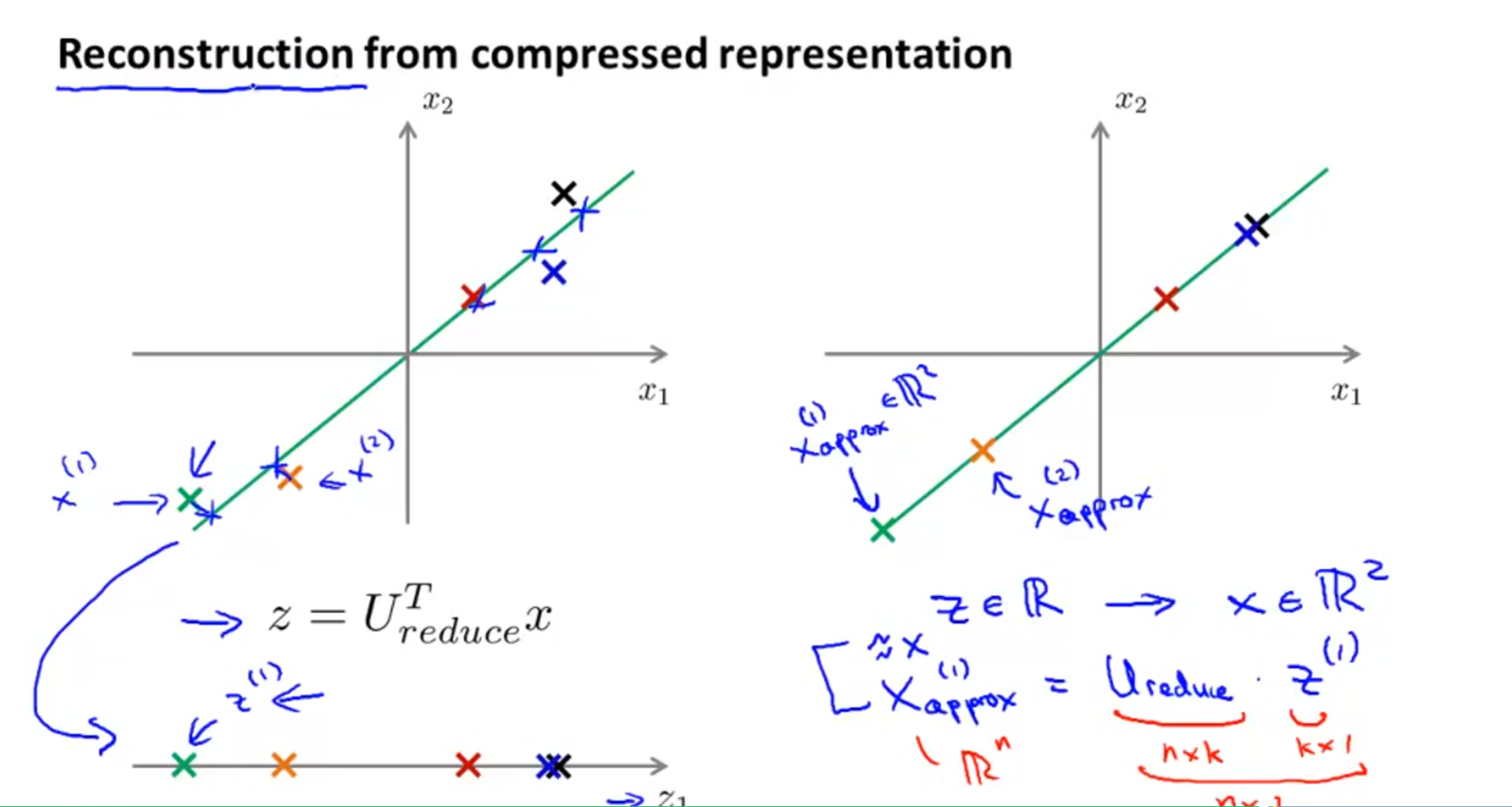
• 위 슬라이드의 왼쪽을 보면 앞에서 다룬 내용인 새로 생성한 저차원의 축에 데이터를 projection하는 방법을 표시해 놓았습니다.
• 만약 다시 고차원의 축으로 데이터를 복원하려면 어떻게 해야 할까요?
• 앞에서 사용한 방법이 행렬의 곱을 이용한 행렬 변환 이었으므로 그 연산 과정을 역으로 이용하면 원본 데이터 근사치를 복원 할 수 있습니다.
  • 위 슬라이드와 같이 \(x_{approx}^{(i)} = U_{reduce} \cdot z^{(i)}\) 로 근사치를 구할 수 있습니다.
  • k차원의 데이터 \(z\)를 다시 n차원으로 복원하였기 때문에 \(x^{(i)}_{approx}\)는 (n x 1)의 크기를 가지는 벡터입니다.

Choosing the Number of Principal Components

• 앞에서 배운 내용을 살펴보면 PCA를 수행할 때 필요한 파라미터는 몇 차원으로 줄일지 선택해야하는 차원의 수 k입니다.
• 경우에 따라서, 예를 들어 data visualization에서는 2차원 또는 3차원으로 차원을 줄일 것이 명확합니다.
• 하지만 data compression 같은 경우에는 몇 차원으로 줄여야 하는 것이 가장 좋은지 명확하지가 않습니다.
• 따라서 차원의 수 k를 정할 때, 수치적으로 적당하다고 생각하는 기준을 정해야 할 필요가 있습니다.
• 아래 내용에서 k 즉 Principal Components의 갯수를 정하는 방법에 대하여 알아보겠습니다.

• 먼저 필요한 두 가지 수치는 위 슬라이드 처럼 Average squared projection error와 Total variation 입니다.
• 앞에서 설명한 바와 같이 PCA를 잘 수행했다는 기준은 projection error를 최소화 하는 것입니다.
• 이전 슬라이드를 참조하면 \(x_{approx}^{(i)} = U_{reduce} \cdot z^{(i)}\)를 이용아여 구할 수 있습니다.
  • 따라서 projection error는 \(x^{(i)}\) 와 \(x_{approx}^{(i)}\) 사이의 거리에 해당합니다.
• 반면 Total variation은 모든 데이터가 원점에서 부터 얼마나 떨어져 있는지를 나타내고 데이터들의 길이 평균이라고 볼 수 있습니다.
• 최종적으로 필요한 Principal components의 갯수는 projection error가 최소가 되도록 하는 조합을 선택해야 하고 이 때의 조합의 구성 성분 갯수가 \(k\)가 됩니다.
• 이 때 나타낼 수 있는 수치가 (Average squared projection error / Total variation) 이고 이 값이 0.01 이하이면 적당한 principal components의 갯수를 선택했다고 보곤 합니다.
• 같은 방법이지만 조금 다르게 표현하면 variance가 99% 정도 만족한다고도 표현할 수 있습니다.

• 위 슬라이드 왼쪽을 보면 앞에서 설명한 방법대로 Principal Components의 갯수를 구하는 방법을 소개하고 있습니다.
• step을 하나 하나 따라가 보면 k=1 일때에는 그럭저럭 할만하지만 k의 갯수가 2, 3, 4, … 증가할 때 마다 연산해야 할 양이 늘어나게 되어서 비효율적으로 느껴지게 됩니다.
• 이 때 동일한 방법을 효율적으로 할 수 있는 방법이 있습니다. 이전 내용에서 본 SVD를 이용하는 방법입니다.
• 공분산을 SVD를 이용하여 분해하였을 때 대각행렬을 보면 위 슬라이드 오른쪽 처럼 분해되어 있음을 알 수 있습니다.
• 대각 행렬의 대각 성분을 이용하면 k개의 성분을 선택하였을 때 variance가 얼마인지를 구할 수가 있습니다.
• 즉, 99%의 variance가 k가 몇일 때 나오는 지 알 수 있으므로 상당히 효율적입니다.

• 다시 한번 정리하면, PCA에서 Principal Component의 갯수는 SVD를 통해 추출한 대각행렬을 이용하여 variance 비율이 크도록 하는 갯수로 정하면 됩니다.

Advice for applying PCA

• PCA를 사용할 수 있는 용도로 Supervised learning에서 학습 속도를 높이기 위해서 feature의 수를 줄일 때 사용할 수 있습니다.
• Supervised learning에서 feature의 갯수가 너무 많은 경우 저차원의 feature에 데이터를 projection하여 차원을 줄이면 학습 속도를 높일 수 있습니다.

• 앞에서 배운 내용을 정리하면 PCA를 사용하는 대표적이 용도는 다음과 같습니다.
  • Compression
    • 데이터를 압축하여 저장 데이터양을 줄입니다.
    • 학습할 데이터의 크기를 줄여 학습 속도를 높입니다.
    • 이 때는 variance의 크기를 관찰하여 Principal component의 갯수 K를 정합니다.
  • Visualization
    • 이 때는 feature의 갯수를 2 ~ 3로 줄여서 데이터의 분포를 관찰합니다.

• 별로 좋지 않은 방법의 PCA 사용 방법은 feature를 줄여서 overfitting을 방지하려는 시도 방법입니다.
• 이 방법은 좋은 결과를 만들 수 있긴 하지만 처음 부터 이 방법을 사용하기 보다는 regularization과 같은 방법을 먼저 시도하는 것이 좋습니다.
  • feature의 갯수를 줄인 다는 것이 데이터의 손실이 발생하기 때문입니다.

• 따라서 supervised learning을 할 때에 PCA를 꼭 써서 학습을 보완하고 싶다면 PCA를 쓰지 않고 학습을 해보고 그 다음 정 필요하다면 PCA를 적용해 보길 권합니다.

code for PCA