Recommender System (Andrew Ng)
2019, Mar 12
- 출처 : Andrew Ng 머신 러닝
-
이번 글에서는 Recommender System에 대하여 알아보도록 하겠습니다.
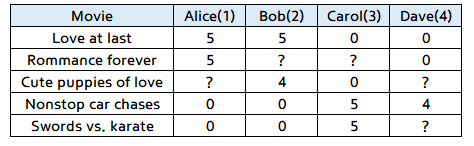
- 위와 같이 영화 평점을 매긴 현황이 있다고 가정하겠습니다.
- 이 때 사용할 notation은 다음과 같습니다.
- \(n_{u}\) : 사람 수
- \(n_{m}\) : 영화의 갯수
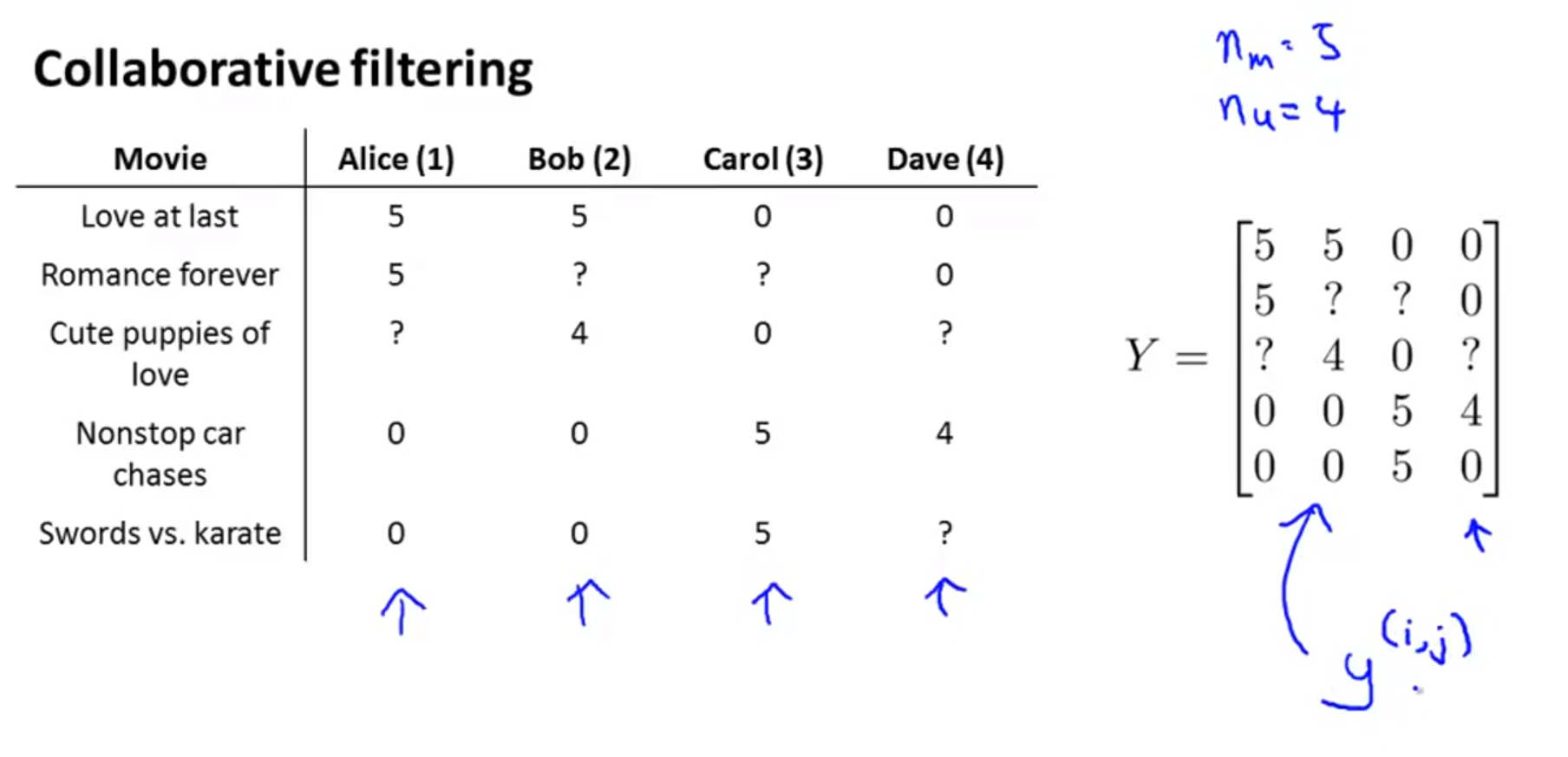
- \(r(i, j)\) : 만약 \(j\)번째 사람이 \(i\)번째 영화를 평가 하였으면 1
- \(y^{(i,j)}\) : \(j\)번째 사람이 \(i\)번째 영화에 매긴 평점 (오직 \(r(i,j) = 1\) 인 경우만 값이 존재함)
- 위 도표에서 ?는 아직 영화를 보지 않았거나 평점이 없는 경우입니다. 이 값을
missing value라고 하고 자동적으로 값을 채워줘야 합니다.- 자동으로 채우는 방법에 대해서는 아래 글에서 다루겠습니다.
Content-based recommender systems
-
먼저 다음과 같은 상황을 가정해 보도록 하겠습니다.
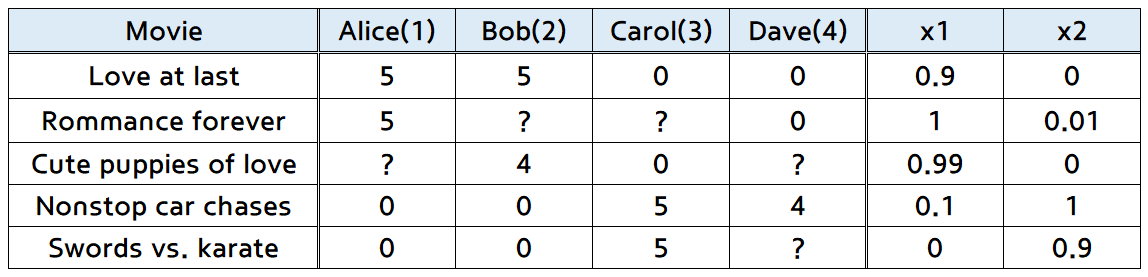
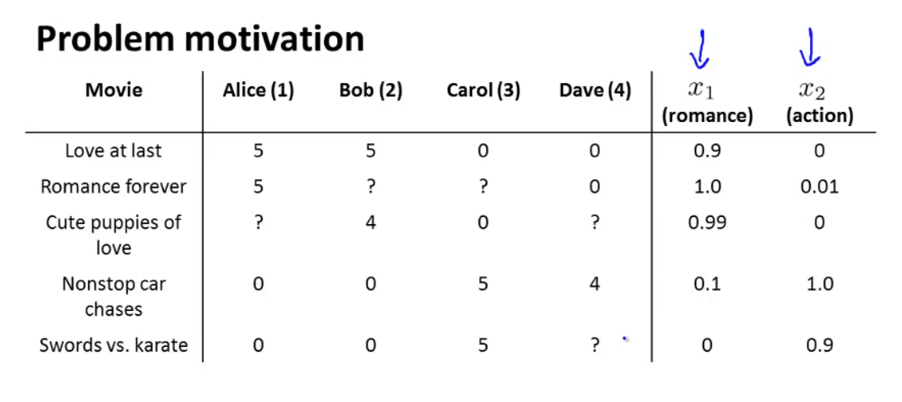
- 추가된 가장 오른쪽 2개의 열 \(x_{1}, x_{2}\)는
feature vector입니다.feature vector는 영화의 성격을 나타냅니다.- 일반적으로
bias에 해당하는 \(x_{0}\)은 따로 표시 않았고 여기에서도 연산할 때에만 추가됩니다.- \(x^{i} = [x_{0}^{i}, x_{1}^{i}, x_{2}^{i}]^{T}\) 에서
- 예를 들어 \(x_{0} = 1\)로 두면,
- \(x^{1} = [1, 0.9, 0]^{T}\)이 됩니다.
- 일반적으로
bias는 feature의 갯수에서 제외합니다.
- 위 슬라이드에서 \(j\) 번째 사람은 파라미터 \(\theta^{j}\)를 학습해야 합니다.
- 이 때 파라미터의 차수는 \(n + 1\)이 됩니다.
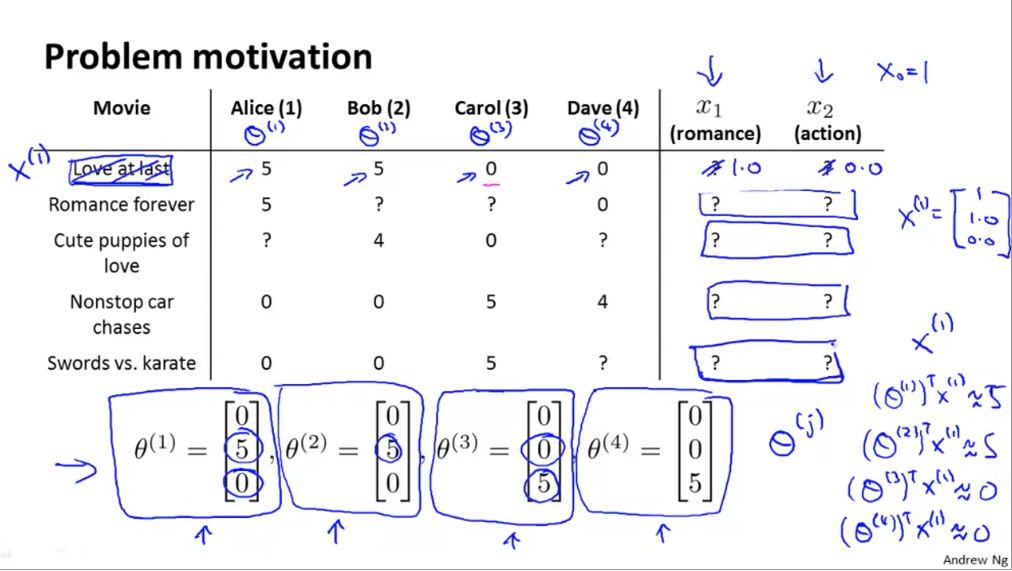
- 예를 들어 1번째 사람의 학습된 파라미터의 결과가 \([0, 5, 0]\) 이라고 가정하겠습니다.
- 1번째 사람이 아직 정하지 못한 점수의 영화는 3번째 영화이므로 3번째 영화의 feature를 가져오겠습니다.
- 즉, \([1, 0.99, 0]\)이 됩니다.
- 따라서 \((\theta^{1})^{T}x^{3} = 4.95\)가 됩니다.
- 벡터의 곱을 이용하기 때문에 당연히 영화의 feature 벡터와 사람의 feature 벡터간의 사이즈가 같아야 합니다.
- 즉, 영화의 feature 벡터의 차원이 bias + feature의 갯수 라고 한다면 사람의 feature 벡터의 차원도 같도록 설정하여 벡터 곱이 가능하도록 만듭니다.
- 상세 용어에 대한 설명은 위 슬라이드와 같습니다.
- \(r(i,j), y^{(i,j)}\)는 각각 평점을 매겼는지 체크하는 값과 평점값에 해당합니다.
- \(\theta{j}\)는 \(j\)번째 사람의 영화 취향에 관한 벡터에 해당합니다.
- \(x^{i}\) 는 i번째 영화의 성격에 관한 feature 벡터에 해당합니다.
- 따라서 \(j\)번째 사람의 벡터와 \(i\) 번째 영화의 feature 벡터의 벡터곱을 하면 \(j\) 번째 사람의 \(i\) 번째 영화에 대한 평점을 예상할 수 있습니다.
- \(m^{j}\)는 \(j\) 번째 사람이 평점을 매긴 영화의 갯수 입니다.
- 위 용어를 참조하여 \(j\) 번째 사람의 \(i\) 번째 영화에 대한 평점을 예측하는 것을 살펴보겠습니다.
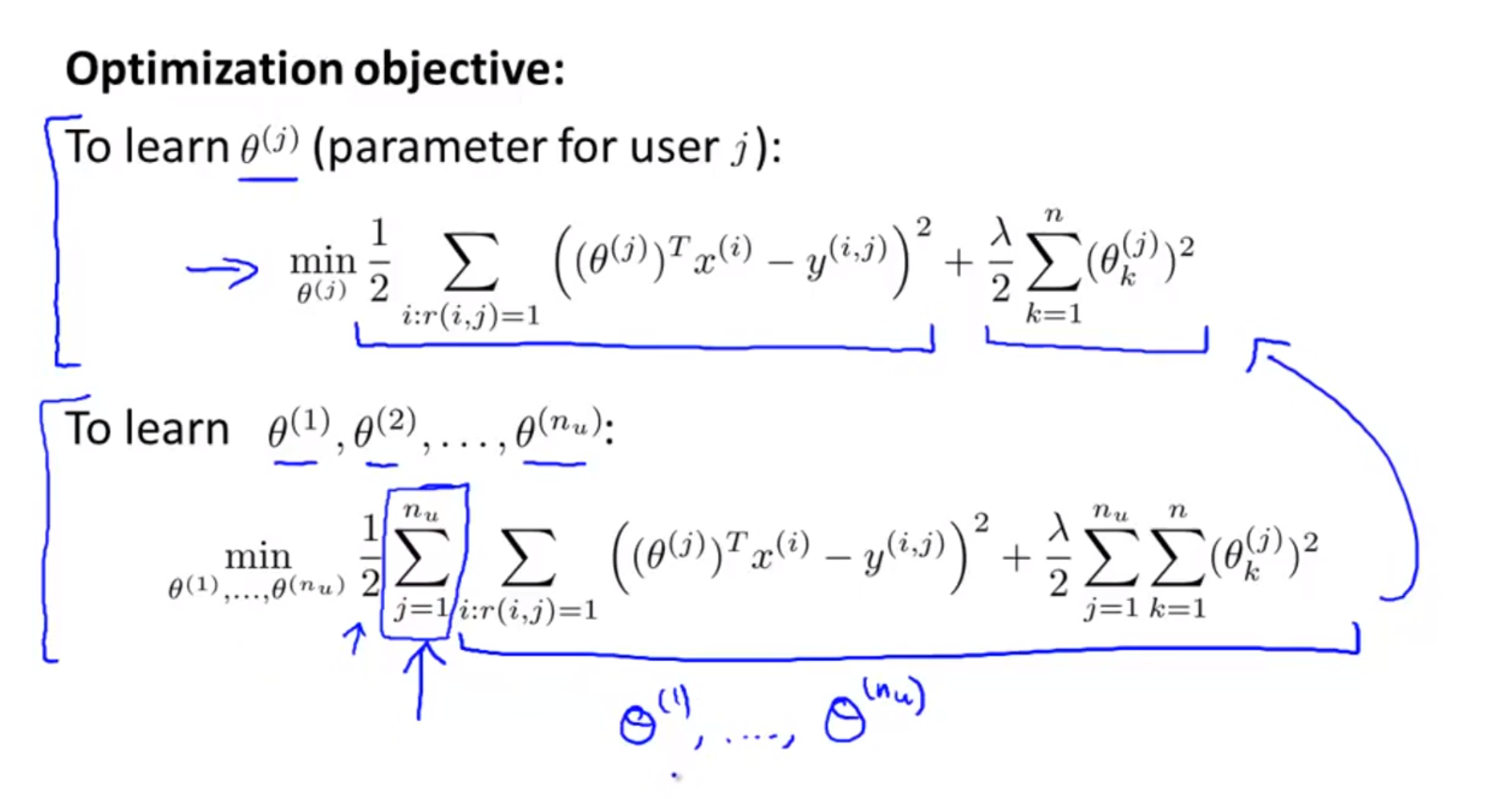
- 위 슬라이드에 있는 식은
linear regression방법 입니다.linear regression의 방법을 이용하여 예측값과 정답의 오차를 줄여나가는 학습 방법을 취합니다. - 그리고 오차함수의 뒤쪽에
regularization도 붙어서overfitting을 줄이는 방법도 적용해 보았습니다. - 위의 오차 함수 식에서 \(m_{j}\)를 지운 것은 상수항으로 학습에 영향이 없기 때문입니다.
- \(\sum_{i:r(i,j) = 1}\)의 뜻은 \(r(i,j) = 1\) 즉, 평점을 매겼을 때에만 계산 과정에 포함시킨다는 의미입니다.
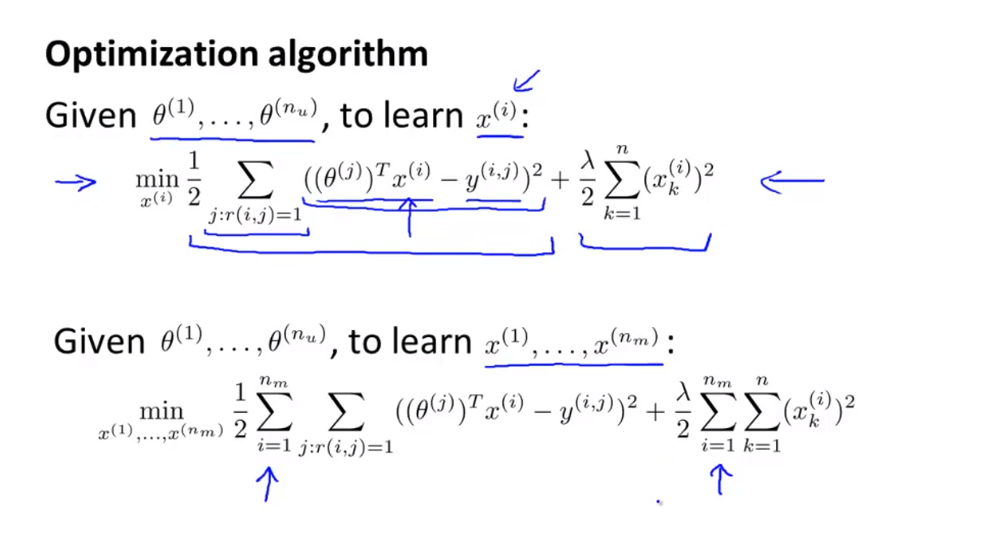
- 위 슬라이드에 있는 식은
- 위 슬라이드의 첫번째 식은 특정 사람(\(j\) 번째 사람)에 관하여 학습하는 것을 보여줍니다.
- 모든 사람들을 대상으로 학습을 하려면 두번째 식을 이용하면 됩니다. 이때 내부 식을 보면 첫번째 식을 좀 더 확장한 것임을 알 수 있습니다.

- 앞의 슬라이드에서 정의한 오차 함수를
gradient descent방법으로 최적화 시킵니다.- 위 슬라이드의 식과 같이 \(\frac{\partial}{\partial \theta_{k}^{(j)} } J(\theta^{(1)}, \cdots , \theta^{(n_{u})} )\)
Collaborative filtering Algorithm
Collaborative filtering algorithm은 앞에서 다른Content-based recommender system에서 feature learning의 내용이 추가된 버전 입니다.- 이 슬라이드를 보면 앞에서 영화의 성격에 해당하는 feature인 \(x_{1}, x_{2}\)의 값이 정해져 있습니다.
- 하지만 현실적으로 이런 각각의 영화마다 feature 를 입력해 주는 것은 쉽지 않은 작업입니다.
- 위 슬라이드에서 \(\theta^{(i)}\)는 각 사람들의 영화 성향에 관한 벡터 입니다.
- 만약 위 슬라이드와 같이 \(\theta^{(i)}\) 에 대한 값은 알려져 있으나 \(x_{i}\) 는 정보가 없는 상황을 가정해 보겠습니다.
- 이와 같이 영화의 feature 벡터에 대한 정보가 없고 각 사람들에 대한 성향의 벡터가 있다면 앞에서 다루었던 것과 반대로 영화의 feature를 유추할 수 있습니다.
- 따라서 이번에 최소화할 오차 함수의 대상은 \(x^{(i)}\)가 됩니다. 따라서 \(x^{(i)}\)에 대하여 편미분을 하면 위와 같이 식을 전개할 수 있습니다.
- 이제 문제를 좀 더 현실적으로 바라보겠습니다. 우리가 필요한 데이터는 사람의 취향에 해당하는 parameter 벡터와 영화의 성격에 해당하는 feature 벡터 두개 입니다.
- 하지만, 일반적으로 이 값을 갖고 있지 않습니다. 대신 완벽하진 않지만(평점이 없는 항목이 있으므로) 사람들이 매겨 놓은 평점이 있습니다.
- 이 평점을 이용하여 supervised learning을 해서 영화와 사람의 벡터를 학습시켜야 합니다.
- 이 때, 두 feature 벡터를 둘 다 모른다면 위 슬라이드와 같이 \(x, \theta\)를 번갈아 가면서 학습할 수 있습니다. 이를 두고
Collaborative filtering이라고 합니다.
- 위 슬라이드와 같이 \(x^{(i)}\)가 주어졌을 때에는, \(\theta^{(i)}\)에 대하여 편미분을 하여 \(\theta^{(i)}\) 값을 구합니다.
- 반대로 \(\theta^{(i)}\)가 주어졌을 때에는, \(x^{(i)}\) 에 대하여 편미분을 하여 \(x^{(i)}\) 값들을 구합니다.
- 위 두가지 방법을 번갈아 가면서 오차함수를 줄여나가면 생각보다 비 효율적일 수 있습니다.
- 따라서 위 두가지 방법을 하나로 묶어서
동시에두 식의 오차함수를 최소화 하는 방법이 필요합니다. - 가장 아래에 있는 식은 \(x^{(i)}, \theta^{(i)}\)들을 동시에 학습하여 오차 함수를 최소화 하는 방법입니다.
- 이전 슬라이드에서는 \(x^{(i)}, \theta^{(i)}\)에 대하여 번갈아 학습하여 오차 함수를 최소화한 반면에 위 슬라이드는 동시에 오차 함수를 최소화 하는 방법에 해당합니다.
- 마지막으로 정리하면
- \(x^{(i)}, \theta^{(i)}\)들을 랜덤 값으로 초기화 해줍니다.
- 오차 함수인 \(J(x^{(1)}, ..., x^{(n_{m}), \theta^{(1)}, ..., \theta^{(n_{u}))\)를 최소하 합니다.
- 마지막으로 학습이 끝나면 predict할 때 파라미터 \(\theta\)와 feature \(x\)를 사용합니다.
Vectorization: Low Rank Matrix Factorization
Collaborative filtering을 적용하기 위하여 평점에 관한 정보를 위의 슬라이드 처럼 행렬로 표현할 수 있습니다.- 앞에서 설명한 바와 같이 ?의 값을 예측하려면 \(\theta\) 와 \(x\)의 곱을 통하여 예측을 해야 합니다.
- 만약 영화를 추천해주려고 하면, 어떻게 하면 될까요? 우리는 영화의 성격에 대한 feature 벡터를 알고 있습니다.
- 즉, \(i, j\) 영화가 있고 그 feature 벡터가 \(x^{(i)}, x^{(j)}\) 라고 할 때, \(\Vert x^{(i)} - x^{(j)} \Vert\) 의 크기가 작을수록 유사한 성격의 영화이므로 추천하기 적합합니다.