Support Vector Machine (Andrew Ng)

2019, Apr 21    

출처 : Andrew Ng 강의

• 이 글에서는 SVM(Support Vector Machine)에 대하여 알아보겠습니다.

Optimization objective

• SVM은 기본적으로 Supervised Learning의 한 방법입니다.
• SVM은 성능도 좋을 뿐만 아니라 복잡한 non-linear function에서 학습할 때에도 좋습니다.

• SVM을 시작하기에 앞서서 logistic regression부터 접근해서 좀 더 확장하는 방법으로 SVM에 대하여 배워보도록 하겠습니다.
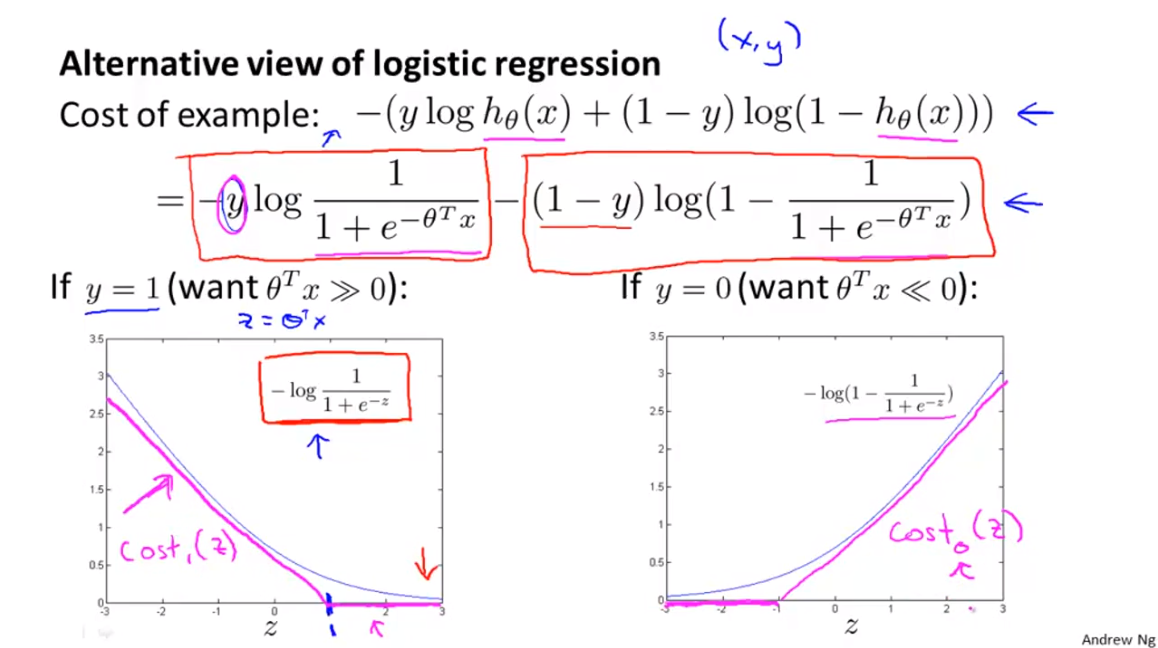
• 위 슬라이드는 기초적인 logistic regression 식을 나타냅니다.
  • 일반적으로 logistic regression에서의 threshold 값은 0.5로 설정하게 됩니다.
  • 따라서 \(z = \theta^{T}x\)의 값이 0보다 크게 되면 prediction은 1이 되고 0보다 작게 되면 prediction은 0이 되게 됩니다.

• logistic regression의 cost function을 살펴보면 위 슬라이드와 같은 식이 도출됩니다.
• logistic regression은 label(y)의 값이 0 또는 1인데 label의 값이 0 또는 1임에 따라서 cost function의 term 하나가 0이 되게 됩니다.
• 먼저 y = 1일 때를 살펴보겠습니다. 왼쪽 아래 슬라이드와 같이 cost function을 표현할 수 있습니다.
  • 이 때 cost function을 접하는 직선을 2개 그어서 근사한 것 처럼 표현해 보겠습니다.
  • 예를 들어 임계값이 \(z = 1\)로 잡으면 \(z\) 값이 점점 증가하다가 \(z = 1\)인 순간부터 cost 값은 0이 되는 구조입니다.
• 반대로 y = 0일 때를 살펴보겠습니다. 오른쪽 아래 슬라이드와 같이 cost function을 나타낼 수 있습니다.
  • 이 때에도 직선으로 cost function에 접하는 근사한 그래프를 그려볼 수 있습니다.

• 앞에서 정의한 각 데이터의 cost function을 모든 데이터에 대하여 정의해 보도록 하겠습니다.
• 위 슬라이드의 식을 보면 \(\sum\) 이 추가 된것을 볼 수 있는데, cost를 모두 합하여 전체 cost를 구하는 것입니다.
• 위 식이 일반적으로 사용하는 식과 다른점은 식을 간편하게 치환하기 위하여 가장 바깥쪽으로 빼두었던 - 부호를 안쪽으로 옮긴 것이 있습니다.
• 이전 슬라이드에서 정의한 바와 같이 직선 2개로 근사한 cost 함수의 그래프를 아래와 같이 간략하게 표현할 수 있습니다.
  • 　\(cost_{1}(\theta^{T}x^{(i)})\) if \(y = 1\)
  • 　\(cost_{0}(\theta^{T}x^{(i)})\) if \(y = 0\)
• 또 간략화 할수 있는 것은 식에 곱해진 \(\frac{1}{m}\) 식입니다. 이 식은 cost function과 regularization에 모두 곱해져 있습니다.
• 이 식을 생략할 수 있는 이유는 위의 슬라이드에서 설명을 하고 있는데, 최소화 하는 optimization 문제에서 곱해진 값은 optimal 값을 찾는 데 영향을 끼치지 않기 때문입니다.
• 마지막으로 regularization에 곱해진 \(\lambda\) 또한 없애주기 위해 두 term에 \(C = \frac{1}{\lambda}\)를 곱해줍니다.
  • 이 또한 optimization 문제를 푸는 데 영향을 주지 않습니다.

• 식을 정리하면 위 슬라이드 처럼 간략하게 표현할 수 있습니다.
• 그러면 다시 이 식을 통하여 prediction을 할 때 \(\theta^{T}x^{(i)}\) 의 값이 0 보다 크면 1로 판단하고 0보다 작으면 0으로 판단하도록 합니다.

Large Margin Intuition

• 앞에서 정리한 SVM의 cost function은 위 슬라이드의 식과 같습니다.
• 이 식과 logistic regression의 식과의 차이점은 Support Vector Machine의 식이 logistic regression의 곡선을 직선으로 근사한 것이라는 점입니다.
  • 여기서 발생하는 차이점은 logistic regression에서는 \(z = \theta^{T}x\)의 값 비교 기준이 0이었으나(0 이상 또는 0 이하) SVM에서는 1과 -1로 바뀌었다는 점입니다.
• 그리고 앞에서 식을 정리하면서 새로 생긴 term인 \(C\)의 크기는 어떤 영향을 미칠까요?

• 위 슬라이드 식의 목적은 cost를 최소한으로 만드는 것 입니다. 즉, 위 식의 값을 최대한 0에 가깝게 줄이는 것입니다.
• 만약 C의 값이 굉장히 크다면 \(\sum\)에 해당하는 값이 0에 가까워 져야 optimization에 가까워집니다.
  • 즉 C의 값이 커질수록 학습할 때 \(\sum\)에 해당하는 값이 더욱 0에 가까워지도록 학습하게 됩니다.

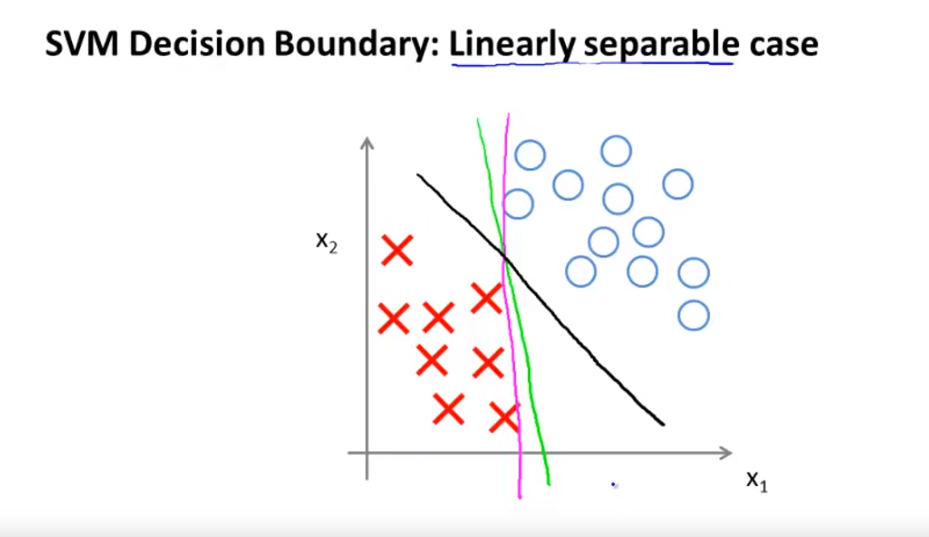
• 이번에는 공간 상에서 SVM이 하는 역할에 대하여 알아보려고 합니다.
• 만약 위 슬라이드의 2차원 공간과 같이 데이터가 분포되어 있습니다. 두 데이터를 나누려고 하는데 어떻게 나누는 것이 좋을까요?
• 두 데이터 부류를 나누는 데에는 상당히 많은 방법이 있습니다.
  • 위 예시를 봤을 때, 자주색 또는 연두색 보다 검은색 선이 더 잘 나눈거 같다고 생각은 드는데요..

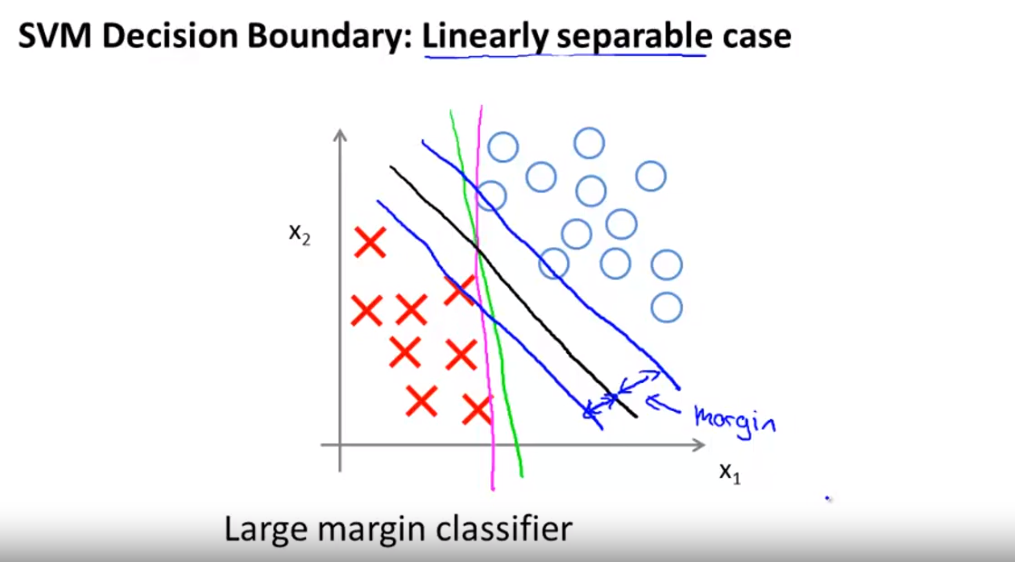
• 그 이유는 검은색 선을 보면 검은색 선에 가장 가까운 데이터와의 거리를 margin 이라고 하는데 검은색 선의 margin이 다른색 선의 margin보다 더 크기 때문입니다.

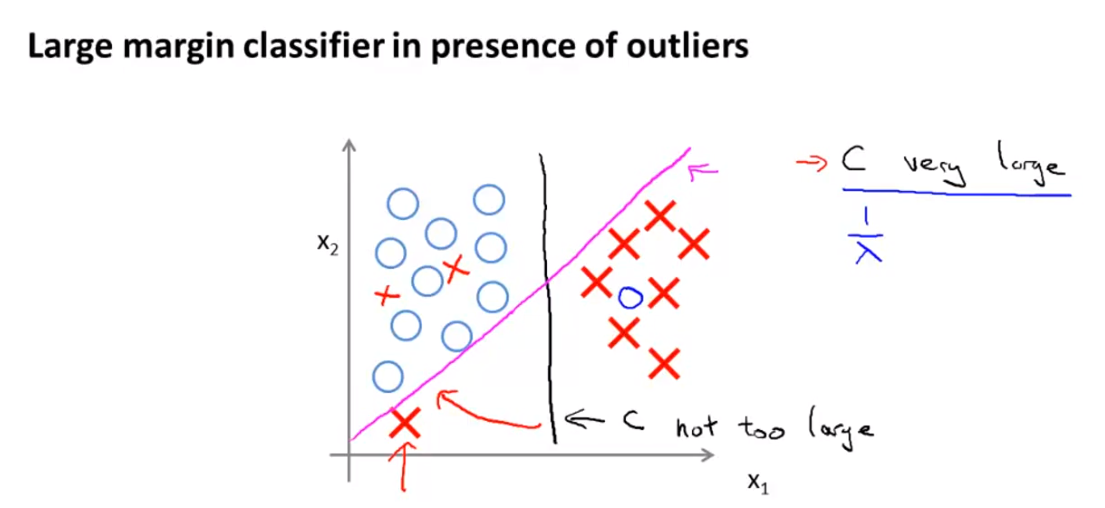
• 앞에서 설명한 C 상수의 크기는 decision boundary에 영향을 미치게 됩니다.
• \(C\)는 정확히 regularization 이라고 볼 수 있습니다. 왜냐하면 \(C = \frac{1}{\lambda}\) 이기 때문입니다.
  • 즉 \(\lambda\)의 값이 너무 커지게 되면(\(C\)의 값이 너무 작아지게 되면) high bais 문제로 인하여 underfitting이 발생할 수 있습니다.
  • 반대로 \(\lambda\)의 값이 너무 작아지게 되면(\(C\)의 값이 커지게 되면) high variance 문제로 overfitting 문제가 발생할 수 있습니다.
• regularization을 적용할 때 적당한 값 \(\lambda\)가 필요하기 때문에 \(C\) 값도한 너무 크지도 작지도 않은 값일 때, 적당한 margin을 가진 line을 구할 수 있습니다.

Mathematics Behind Large Margin Classification

• 이번에는 SVM에서 decision boundary가 어떻게 큰 margin을 가지는 지 살펴보도록 하겠습니다.

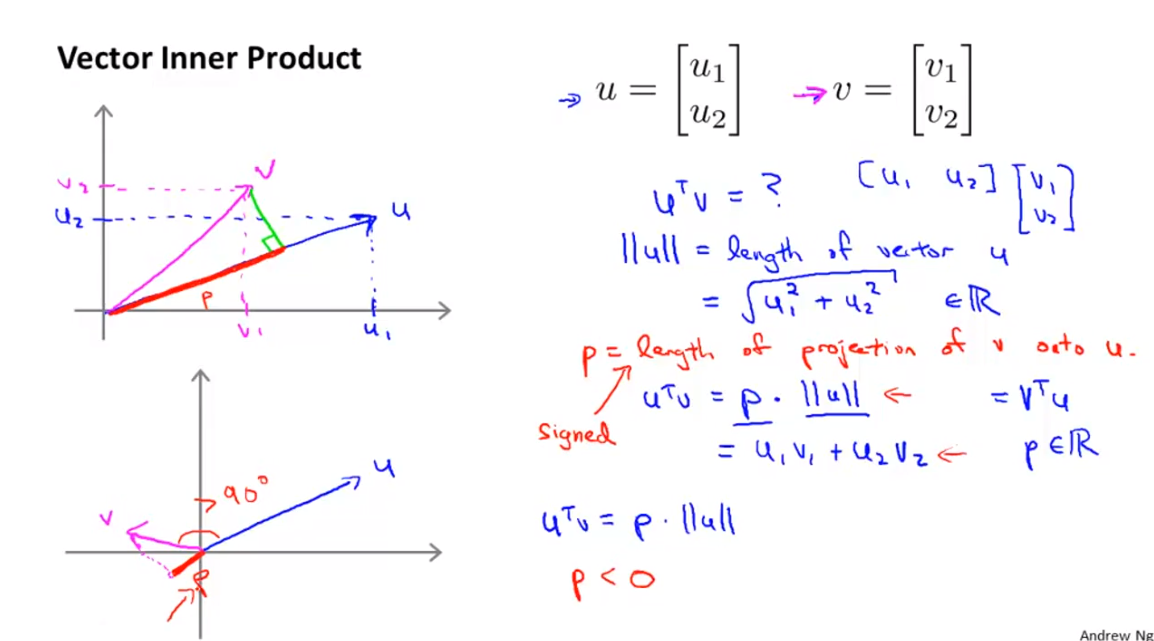
• 먼저 vector의 inner product의 의미에 대하여 살펴보겠습니다.
• 내적(inner product)는 두 벡터 \(u, v\)가 있을 때, 한 벡터를 다른 벡터에 정사영 시켰을 때 생기는 선분의 길이와 정사영된 벡터의 길이의 곱으로 표현할 수 있습니다.
  • 위 예제에서 보면 벡터 \(u\)에 벡터 \(v\)를 정사영 시켰고, 이 때 \(p\) 길이의 선분이 생겼습니다. 이 때 내적의 결과는 \(p\)와 \(\Vert u \Vert\) 의 곱 입니다.
• 이 때 \(p\)의 크기는 벡터 \(u, v\)의 사이 각에 따라 달라지는 것을 알 수 있습니다.
  • 만약 사이각의 크기가 90도가 넘어가면 \(p\) 값은 음수가 되기도 합니다.

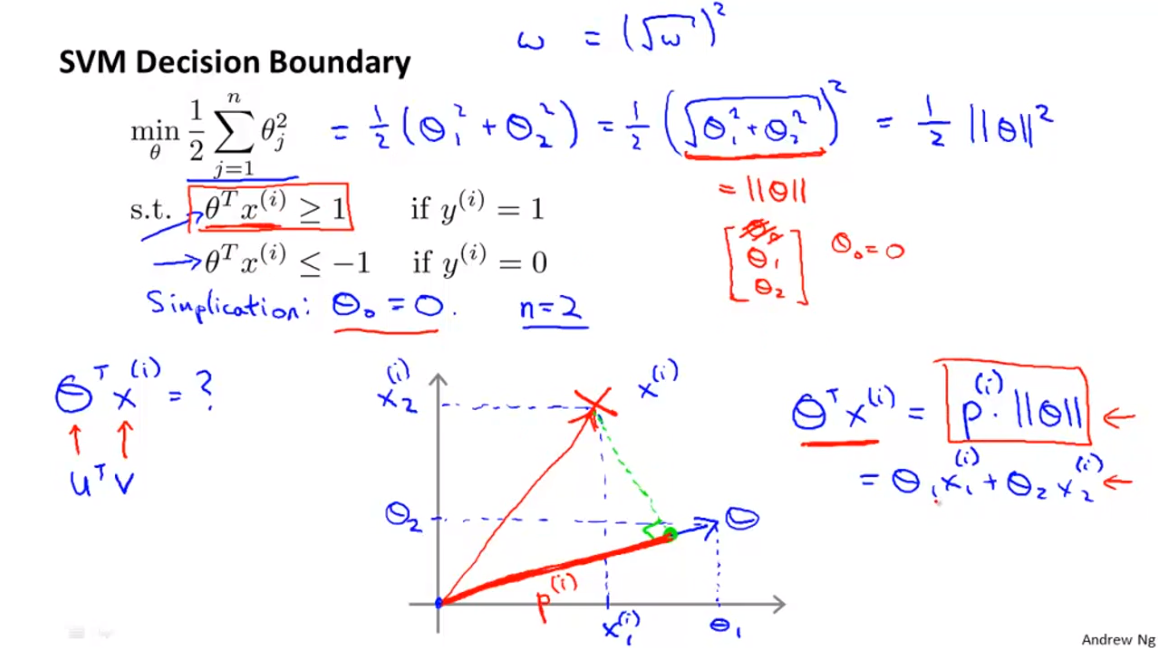
• 위 슬라이드의 식이 SVM의 objective function이라고 가정해 보겠습니다. 또한 식을 간단하게 하기 위하여 bias인 \(\theta_{0}\)은 없다고 가정하겠습니다.
  • bias는 간단하게 0으로 나타내기로 하였으므로 2차원 평면에서 decision boundary의 절편은 0으로 간단하게 표시할 수 있습니다.
• 앞에서 살펴본 벡터의 내적 개념을 이용하여 \(\theta\) 와 \(x^{(i)}\)에 대하여 적용해 보겠습니다.
• 위 슬라이드의 그래프를 보면 \(x^{(i)}\) 를 \(\theta\) 에 사영시킵니다.

• 앞에서 다룬것 처럼 Object function을 위 슬라이드 처럼 정의해 보았습니다.
• 그리고 벡터 내적의 정의에 따라서 \(p^{(i)} \cdot \Vert \theta \Vert \ge 1\) 또는 \(p^{(i)} \cdot \Vert \theta \Vert \le -1\) 로 표현할 수 있습니다.
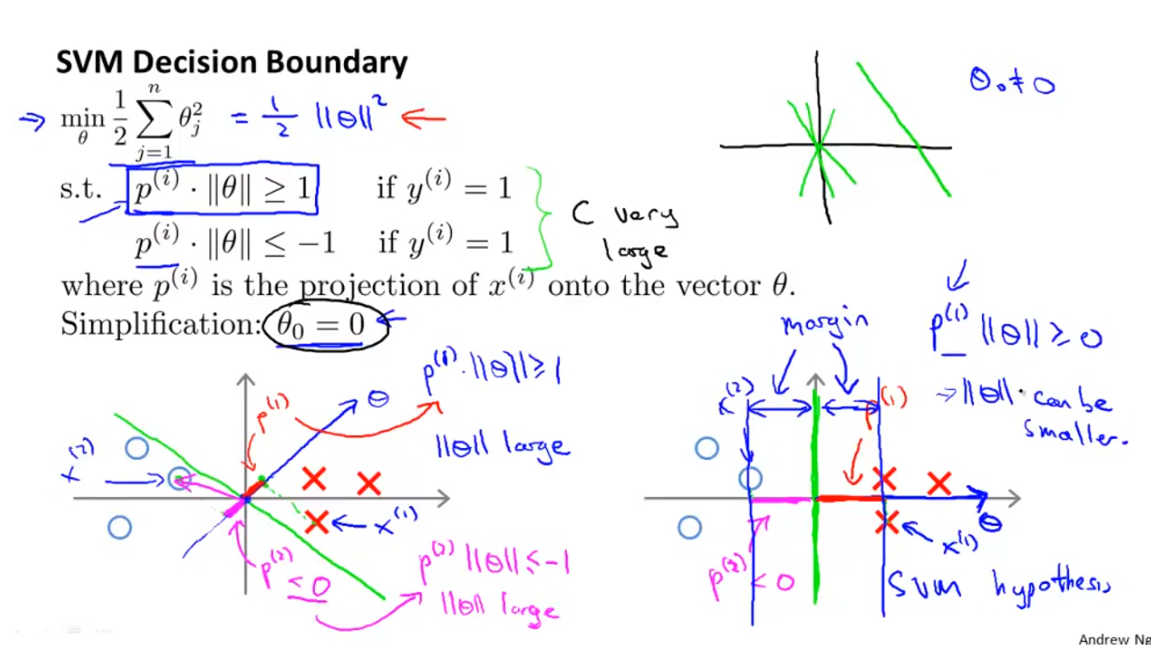
• decision boundary와 theta는 직교 관계를 가집니다. 이 관계를 이용해서 어떻게 margin이 큰 decision boundary를 찾는지 설명해 보겠습니다.
• 위 슬라이드의 왼쪽 아래 그래프를 보면 약간 아슬아슬한 decision boundary를 볼 수 있습니다.
  • 이 boundary와 직교 관계를 가진 벡터를 \(\theta\)라고 하겠습니다.
  • 먼저 \(\theta\)의 \(\theta_{0}\)은 0이라고 가정하였기 때문에 원점을 지나는 것을 알 수 있습니다.
  • 이 예제와 같은 경우 \(\theta\)와 데이터의 정사영 관계를 보면 \(p\)의 값이 작은 것을 확인할 수 있습니다.
  • 따라서 \(p^{(i)} \cdot \Vert \theta \Vert \ge 1\) 식에서 보면 \(p^{(i)}\) 값이 작으므로 \(\Vert \theta \Vert\) 값이 커져야 함을 알 수 있습니다.
  • 반대로 \(p^{(i)} \cdot \Vert \theta \Vert \le -1\) 의 관계에서도 \(p^{(i)}\) 값이 0과 가까우므로 \(\Vert \theta \Vert\) 값이 커져야 합니다.
• 이번에는 오른쪽 아래 그래프를 보면 좀 더 적합한 decision boundary가 있음을 알 수 있습니다.
  • 왼쪽 그래프와 동일한 방법으로 오른쪽 그래프를 접근해 보면 \(p\) 값이 왼쪽 그래프 케이스 보다 큰 것을 알 수 있습니다.
• 잘 생각해 보면 사영한 값 \(p\)는 margin임을 알 수 있습니다. 즉 \(p\) 값이 최대하 커지도록 \(\theta\)를 학습하면 margin이 큰 decision boundary를 찾을 수 있습니다.

Kernerls 1

• 이번에는 SVM에서 사용하는 Kernel 기법에 대하여 알아보도록 하겠습니다. Kernel 기법을 이용하면 좀 더 복잡한 non-linear classifier를 만들 수 있습니다.

• 만약 위와 같은 데이터 분포가 있다면 Non-linear boundary를 이용하여 positive/negative 데이터를 나누어야 합니다.
• 위의 슬라이드의 식과 같이 Non-linear boundary를 만들 수 있다면 만약 \(x_{1}, x_{2}, ...\) 등과 파라미터가 곱해졌을 때, 양수이면 1 그렇지 않으면 0을 취할 수 있습니다.
  • SVM에서 다룰 Kernel은 이 기본적인 분류 기법에서 출발할 수 있습니다.
• 그런데 위 식을 보면 기존에 사용하였던 데이터 값인 \(x_{i}\) 대신에 \(f_{i}\) 가 있음을 알 수 있습니다.
  • 과면 \(f_{i}\)는 무슨 의미일까요?

• 위 슬라이드에서는 \(f_{i}\)를 정해보는 한가지 예제를 들어보겠습니다.
• 기존에 존재하는 feature인 \(x_{1}, x_{2}\)가 있다고 가정하였을 때, 이 공간에 분포하는 포인트 \(l_{1}, l_{2}, l_{3}\) 가 있다고 생각해 보겠습니다.
  • 이 때 \(l_{i}\) 들을 landmark라고 해보겠습니다.
• 이 때, \(f_{i} = similarity(x, l^{(i)})\) 로 표현할 수 있습니다. 이 식을 Kernel 이라고 부릅니다.
  • 위 슬라이드에서는 예제로 \(f_{i} = exp( \frac{ \Vert x - l^{(i)} \Vert}{2\sigma^{2}})\)으로 kernel 식을 정의하였습니다.
  • 위 식의 kernel을 Gaussian kernel이라고 합니다.
  • 위 식 중 \(\Vert x - l^{(i) \Vert\) 는 데이터 x와 landmark간의 유클리디안 거리를 나타냅니다.