확률과 통계 기초

참조 : 패턴 인식 (오일석)

확률 기초

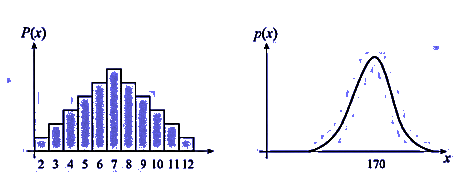
Discrete & Continuous Probability

주사위를 던졌을 때 3이 나올 확률(probability)는 \(\frac{1}{6}\) 입니다.
이것을 기호로 표시하면 \(P(X = 3) = \frac{1}{6}\)
여기서 \(X\)는 랜덤 변수(random variable) 라고 하고 \(X\)는 discrete 값을 가집니다.
이 때 확률 분포는 왼쪽 그래프와 같이 PMF(PMF = probability mass function)로 나타냅니다. PMF에서는 각 랜덤 변수에 해당하는 확률(사각형 면적)이 존재합니다. 모든 랜덤변수에 해당하는 확률을 다 더하면 1이 됩니다. 간단히 면적의 총합이 1이라고 생각할 수 있습니다.
반면 사람 키를 생각해보면 주사위와는 조금 다릅니다. continuous 한 값을 가집니다.
이 때 확률 분포는 오른쪽 그래프와 같이 PDF(PDF = probability density function)로 나타냅니다. PDF의 그래프를 보면 PMF와는 조금 다릅니다. 랜점 변수들이 연속적인 값을 가지기 때문에 PMF와 달리 특정 랜덤 변수의 확률값은 0에 수렴합니다. 대신에 영역을 통해 나타낼 수 있습니다. 오른쪽 그래프 기준으로는 165 이상 170이하 구간에 대한 확률값은 면적으로 구할 수 있습니다.
정리하면 PDF에서는 PMF와 달리 각 확률 변수에 해당하는 확률은 0이고(즉, 면적이 없고) 영역을 통해 확률을 나타낼 수 있으며 총 면적의 합은 1이 됩니다.

Basic Bayes Rule

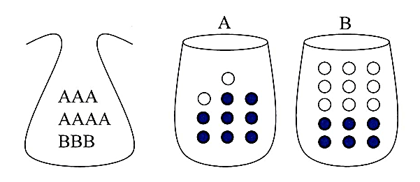
먼저 간단하게 Bayes Rule을 게임을 통하여 알아보도록 하겠습니다.
주머니에는 A 카드 7장과 B카드 3장이 있습니다. 그리고 A, B 상자에는 각각 하얀공과 파란 공이 있습니다.
① 먼저 주머니에서 카드 한장을 뽑고, ② 뽑은 카드에 맞는 상자에서 공을 뽑습니다. 그리고 공의 색을 확인한 뒤 다시 집어 넣습니다. (복원 추출)
그러면 문제를 풀 때 먼저 랜덤 변수를 정해야 합니다.

랜덤 변수 \(X\) : 주머니에서 뽑은 용지 (\(X \in \{A, B\}\))
랜덤 변수 \(Y\) : 상자에서 뽑은 공 (\(Y \in \{하얀, 파란\}\))

이 때 상자 A가 선택될 확률은 다음과 같이 표현할 수 있습니다.

\[P(X = A) = P(A) = \frac{7}{10}\]

상자 A에서 하얀 공이 뽑힐 확률은 어떻게 될까요? 주머니에서 A라 쓰인 용지를 뽑았다는 조건 하에 확률을 따져보겠습니다. 조건하에 따진다고 하여 조건부 확률(conditional probability) 라고 합니다.

\[P(Y = 하얀 \vert X = A) = P(하얀 \vert A) = \frac{2}{10}\]

상자는 A 이고 공은 하얀공이 뽑힐 확률 \(P(A, 하얀)\)은 얼마일까요? 두 가지 서로 다른 사건이 동시에 일어날 확률입니다.
이 경우를 joint probability 라 하고 joint probability는 두 확률의 곱으로 구합니다.
또한, 다음 계산 법을 product rule 이라고 합니다.

\[P(A, 하얀) = P(하얀 \vert A) P(A) = (\frac{2}{10})(\frac{7}{10}) = \frac{7}{50}\]

하얀 공이 나올 확률은 어떻게 될까요? 이 때 가능한 경우의 수는 다음과 같습니다.
① A가 선택되고 하얀 공이 나오는 경우, ② B가 선택되고 하얀 공이 나오는 경우
두 경우의 확률을 더하면 답이 되며 이런 계산 방법을 sum rule이라고 합니다.
이런 방식으로 구한 확률 \(P(하얀)\) 을 marginal probability 라고 합니다.

\[P(하얀) = P(하얀 \| A)P(A) + P(하얀 \| B)P(B) = (\frac{2}{10})(\frac{7}{10}) + (\frac{9}{15})(\frac{3}{10}) = \frac{8}{25}\]

두 랜덤 변수가 서로 영향을 미치지 못하였다면 independent 한다고 합니다.
- 독립인 두 랜덤 변수는 \(P(X,Y) = P(X)P(Y)\) 를 만족해야 합니다.
- 위의 예제에서는 \(P(X,Y) \neq P(X)P(Y)\) 이므로 독립이 아닙니다.
  - 주머니가 공의 색깔에 영향을 미치고 있다는 뜻입니다.

P(A)와 P(B)를 prior event 라고 합니다.
- 확률 실험에서 상자 선택과 공 선택이라는 event가 연이어 일어나는데, 공 선택 전에 상자 선택이 일어나기 때문입니다.

만약 하얀 공이 뽑혔을 때, 하얀 공이 어느 상자에서 나왔는지를 확률적으로 맞추어 보겠습니다.
- 상자 A의 하얀 공 확률 \(P(하얀\|A) = \frac{2}{10}\)
- 상자 B의 하얀 공 확률 \(P(하얀\|B) = \frac{9}{15}\)
- 이렇게 비교할 경우 조건부 확률 \(P(Y\|X)\)를 사용한 셈이고, Y는 이미 관찰되어 하얀으로 고정되어 있어 X에 따라 확률을 계산합니다.
- 이 때 조건부 확률을 likelihood 라고 합니다.
  - 하지만 \(P(하얀 \| A) + P(하얀 \| B) \neq\) 1 이므로 probability의 개념은 아닙니다.

하지만 likelihood만 고려한다면 주머니에서의 카드 A와 B의 분포가 무시됩니다.
- 만약 A가 1억장 , B가 1장이라면 likelihood만 고려한 B가 더 가능성이 높다고 할 수 있을까요?
- A가 1억장인 극단적인 케이스에서 생각해 보면 prior event \(P(X)\) 와 likelihood \(P(Y\|X)\) 모두를 고려해야만 합리적인 선택을 할 수 있습니다.

위에서 살펴본 내용으로 보면 likelihood 만으로 판단하기 보다는 하얀 공이 관찰된 조건 하에서 어떤 상자에서 나왔는지를 알아내는 것이 더 적합해 보입니다.
- 즉, \(P(A \| 하얀)\) vs \(P(B \| 하얀)\) 을 비교하는 것이 더 맞아 보입니다.
- \(P (X \| Y)\)를 사용하려고 하고 이 때 Y가 고정이 되고 X에 따라 확률을 계산합니다.
- 이 조건부 확률을 posterior probability 라고 합니다.
  - 사건 Y가 일어날 이후에 따지는 확률이므로 posterior 라고 불리게 됩니다.

posterior probability \(P(X\|Y) = \frac{P(Y\|X)P(X)}{P(Y)} = \frac{likelihood \ \times \ prior}{P(Y)}\)

주변 확률 \(P(Y)\)의 경우 \(X \in \{A,B\}\) 이므로 \(P(Y) = P(Y\|A)P(A) - P(Y\|B)P(B)\) 가 됩니다.
- 따라서, \(P(Y) = \sum_{X} P(Y\|X)P(X)\) 이 됩니다.

이제 Bayes 정리를 이용하여 posterior probability를 다음과 같이 정리할 수 있습니다.
- prior event : P(X)
  - 주머니에서 카드 A, B를 뽑는 사건에 대한 확률
- posterior event : P(Y)
  - 상자에서 하얀 공을 거낼 확률 : marginal probability
  - marginal probability = \(\sum likelihood \ \times \ prior\)
  - 따라서 \(P(하얀) = P(하얀\|A)P(A) + P(하얀\|B)P(B) = \frac{2}{10}\frac{7}{10} + \frac{9}{15}\frac{3}{10} = \frac{8}{25}\)
- likelihood : \(P(Y\|X)\)
  - \(P(하얀\|A) = \frac{2}{10}\) : A상자에서 하얀공을 꺼낼 확률
  - \(P(하얀\|B) = \frac{9}{15}\) : B상자에서 하얀공을 꺼낼 확률
- posterior probability \(P(X \| Y) = \frac{likelihood \ \times \ prior}{P(Y)}\)
  - 하얀 공이 나왔을 때, A 상자에서 꺼냈을 확률 : \(P(A\|하얀) = \frac{P(하얀 \| A) \times P(A)}{P(하얀)} = 0.4375\)
  - 하얀 공이 나왔을 때, B 상자에서 꺼냈을 확률 : \(P(B\|하얀) = \frac{P(하얀 \| B) \times P(B)}{P(하얀)} = 0.5625\)
- posterior probability에 따라서 신뢰도 0.5625로 B에서 나왔다고 할 수 있습니다.
  - 이와 같이 confidence를 제공할 수 있습니다.

평균과 분산

지금까지 기본적인 Bayes 정리를 알아보면서 likelihood와 posterior probability에 대하여 알아보았습니다. 이제 랜덤 변수의 통계적 특성에서 가장 많이 쓰이는 평균(mean)과 분산(variance)에 대하여 알아보겠습니다. 사실, 통계 값을 계산할 때에는 2가지 상황이 있습니다.

확률 분포가 명시적인 상황
확률 분포 대신 샘플 집합이 있는 상황
- 샘플들이 어떤 확률 분포로 부터 추출되었으므로 샘플 집합이 확률 분포를 암시적으로 내포하고 있는 상황

확률 분포가 주어진 상황

확률 분포가 주어진 상황에서는 이산인 경우와 연속인 경우에 대하여 나누어 생각할 수 있습니다.

이산(discrete) 확률 분포
- 평균 \(\mu = \sum_{x}xP(x)\)
- 분산 \(\sigma^{2} = \sum_{x}(x-\mu)^{2}P(x)\)
연속(continuous) 확률 분포
- 평균 \(\mu = \int_{\infty}^{\infty}xp(x) dx\)
- 분산 \(\sigma^{2} = \int_{\infty}^{\infty}(x-\mu)^{2}p(x)dx\)

이산 확률 분포에서는 \(P(x)\), 연속 확률 분포에서는 \(p(x)\)로 구분하여 표기하였습니다.

이산 확률 분포가 주어진 경우 평균과 분산 계산

두 개의 주사위를 던지고 나온 눈의 합을 랜덤 변수 \(x\)라 하면 평균과 분산은 다음과 같습니다.
- 확률 분포 \(P(x_{2}) = \frac{1}{36}, P(x_{3}) = \frac{2}{36} , P(x_{4}) = \frac{3}{36}, P(x_{5}) = \frac{4}{36}, P(x_{6}) = \frac{5}{36}, P(x_{7}) = \frac{6}{36}\)
  \(P(x_{8}) = \frac{5}{36}, P(x_{9}) = \frac{4}{36}, P(x_{10}) = \frac{3}{36}, P(x_{11}) = \frac{2}{36}, P(x_{12}) = \frac{1}{36}\) 입니다.
- 평균 \(\mu = \sum_{i=2}^{12}i \times P(x_{i}) = 7\)
- 분산 \(\sigma^{2} = \sum_{i=2}^{12}(i - \mu)^{2} \times P(x_{i}) = 5.83\)

이제 확률 분포는 모르고 샘플 집합만 주어진 상황을 생각해 보겠습니다.
- 샘플의 갯수는 N, i번째 샘플을 \(x_{i}\) 로 표기하겠습니다.
- 충분히 많은 샘플을 확보하여 \(N \to \infty\) 이 되면 실제 확률 분포와 가까와 진다는 통계적 정리에 따라
  - 평균 \(\mu = \frac{1}{N}\sum_{i=1}^{N}x_{i}\)
  - 분산 \(\sigma^{2} = \frac{1}{N-1}\sum_{i=1}^{N}(x_{i} - \mu)\)
    - 분산을 구할 때, N이 아니라 N-1로 나누어 주었습니다. 바이어스의 영향으로 N-1로 나누어 주어야 합니다.
    - 참조 : https://gaussian37.github.io/ml-question-q6/

샘플 집합이 주어진 상황

샘플 집합이 주어진 경우 평균과 분산

두 개의 주사위의 합에 대한 확률 분포를 모른다고 가정하고 실제 주사위를 2개를 10번 던져서 나온 실험을 이용하여 평균과 분산을 구해보겠습니다.
확률 분포

실험	1	2	3	4	5	6	7	8	9	10
나온수	(3,2)	(3,5)	(6,6)	(5,1)	(1,6)	(4,5)	(6,4)	(4,2)	(6,1)	(4,1)
랜덤 변수 x	x1 = 5	x2 = 8	x3 = 12	x4 = 6	x5 = 7	x6 = 9	x7 = 10	x8 = 6	x9 = 7	x10 = 5

평균 : \(\mu = \frac{1}{10}\sum_{i=1}^{10} x_{i}= 7.5\)
분산 : \(\sigma^{2} = \frac{1}{9}\sum_{i=1}^{10}(x_{i} - \mu)^{2} = 5.16667\)

랜덤 변수가 여러개가 주어진 상황

랜덤 변수 한개의 통계적 분석은 feature 하나를 분석한 것과 같습니다.
현실 데이터에서는 여러개의 랜덤 변수가 랜덤 벡터를 구성하는 경우가 많음
랜덤 벡터 : \(x = (x_{1}, x_{2}, ... , x_{d})^{T}\)
평균 벡터 : \(\mu = (\mu_{1}, \mu_{2}, ... , \mu_{d})^{T}\)
- 평균 벡터를 구하는 방법은 아래 3가지 입니다.
- 이산 확률 분포 : \(\mu = \sum_{x} xP(x)\)
- 연속 확률 분포 : \(\mu = \int_{R^{d}} xP(x) dx\)
- 샘플 집합 : \(\mu = \frac{1}{N}\sum_{i=1}^{N}\)

공분산

중요한 통계적 특성으로 \(x_{i}, x_{j}\) 사이의 공분산 \(\sigma_{ij}\)(covariance)이 있습니다.